
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическое определение вероятностей.Содержание книги Поиск на нашем сайте
ОПРЕДЕЛЕНИЕ (классическое определение вероятности). Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события А определяется формулой:
где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания. Свойство 1. Вероятность достоверного события равна единице. Свойство 2. Вероятность невозможного события равна нулю. Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей. Итак, вероятность любого события удовлетворяет двойному неравенству 0 Основные понятия теории вероятностей. Событием является любой факт, который можно констатировать в результате наблюдения или опыта. События, которые могут произойти в результате опыта, можно подразделить на три вида: а) достоверное событие – событие, которое всегда происходит при проведении опыта; б) невозможное событие – событие, которое в результате опыта произойти не может; в) случайное событие – событие, которое может либо произойти, либо не произойти. Случайные события обычно обозначают большими буквами латинского алфавита A, B, C и т.д. Случайные события могут быть: · несовместимыми; · совместимыми. События A, B, C … называют несовместимыми, если в результате одного испытания может наступить одно из этих событий, но невозможно наступление двух или более событий. Если наступление одного случайного события не исключает наступление другого события, то такие события называют совместимыми. Если в каждом наблюдении (испытании) должно произойти одно и только одно из несовместимых случайных событий, то эти события составляют полное множество (систему) событий. Достоверным событием является наступление хотя бы одного события из полного множества событий. Если события, образующие полное множество событий, попарно несовместимы, то в результате наблюдения может наступить только одно из этих событий. Если полное множество событий состоит только из двух несовместимых событий, то их называют взаимно противоположными или альтернативными событиями. События называют равновозможными, если ни у одного из них нет объективных преимуществ. Такие события также составляют полное множество событий. Это значит, что в результате наблюдения или испытания определенно должно наступить по меньшей мере одно из равновозможных событий.
Элементы комбинаторики. При вычислении вероятностей часто приходится использовать некоторые формулы комбинаторики – науки, изучающей комбинации, которые можно составить по определенным правилам из элементов некоторого конечного множества. В теории вероятностей часто используют размещения, перестановки и сочетания. Если дано множество Перестановки – это комбинации, составленные из всех п элементов данного множества и отличающиеся только порядком их расположения. Число всех возможных перестановок Размещения – комбинации из т элементов множества, содержащего п различных элементов, отличающиеся либо составом элементов, либо их порядком. Число всех возможных размещении Сочетания – неупорядоченные наборы из т элементов множества, содержащего п различных элементов (то есть наборы, отличающиеся только составом элементов). Число сочетаний
|
||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.116 (0.008 с.) |

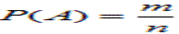
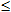 P(A)
P(A) 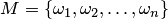 , торазмещением (сочетанием) из
, торазмещением (сочетанием) из 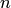 элементов по
элементов по 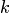 называется любое упорядоченное (неупорядоченное) подмножество
называется любое упорядоченное (неупорядоченное) подмножество 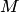 . При
. При 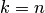 размещение называется перестановкой из
размещение называется перестановкой из 


