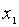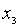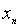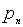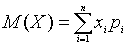Числовые характеристики дискретной случайной. Математическое ожидание, дисперсия.

Закон распределения полностью характеризует случайную величину. Однако часто построение закона или ряда распределения представляет весьма трудоемкую задачу, либо закон распределения неизвестен вовсе. На практике иногда бывает достаточно описать случайную величину «суммарно», указав ее отдельные числовые параметры, до некоторойстепени характеризующие существенные черты распределения случайной величины. К таким параметрам можно отнести среднее значение, около которого группируются возможные значения случайной величины; число, характеризующее степень разбросанности значений случайной величины относительно среднего и др. Назначение таких характеристик – выразить компактно, в сжатой форме наиболее существенные особенности распределения. Все эти характеристики называются числовыми характеристиками случайной величины.

 

Пусть случайная величина Х задана таблицей распределения

 

X				…		…
p				…		…

 

Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее возможных значений на соответствующие вероятности :

Математическое ожидание называют также средним значением случайной величины Х, подчеркивая статистический смысл понятия, или центром распределения случайной величины Х (по аналогии с понятием центра тяжести для системы материальных точек).

Свойства математического ожидания:

1) если случайная величина Х принимает постоянное значение Х=С= =const, то М(С)=С;

2) М(СХ)=СМ(Х), С = const;

3) Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий: M(X+Y)=M(X)+M(Y);

4) Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: M(X×Y)=M(X)×M(Y).

Наряду с характеристиками положения большую роль играют характеристики рассеяния. Рассеяние случайной величины Х связано с отклонением этой величины от ее центра распределения М(Х). Чтобы учитывать отклонения противоположных знаков, удобно рассматривать квадраты отклонений.

Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Свойства дисперсии.

Свойство 1. Дисперсия постоянной равна нулю. По определению

Свойство 2. Постоянную можно выносить за знак дисперсии с возведением в квадрат.

Свойство 3. Если случайные величины Х и У независимы, то