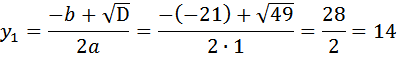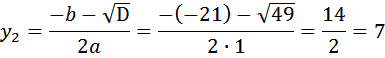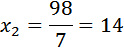Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Площадь трапеции равна произведению средней линии на высоту.Содержание книги
Поиск на нашем сайте
Ответ: 6
27595. Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
Здесь нужно помнить о том, что если линейные размеры фигуры увеличиваеются в k раз, то площадь фигуры увеличивается в k2 раз. Периметр увеличился в
Ответ: 50 27596. Найдите площадь круга, длина окружности которого равна
Формула площади круга:
Формула длины окружности:
Для того, чтобы найти площадь круга, необходимо найти радиус круга, его мы можем найти из формулы длины окружности:
Подставим найденный радиус в формулу круга и найдём площадь:
Ответ: 0,25
27597. Площадь круга равна
Формула площади круга:
Формула длины окружности:
Это обратная задача. Из формулы площади круга найдём радиус:
Значит, длина окружности равна:
Ответ: 2
27598. Найдите площадь сектора круга радиуса
Формула площади круга:
Сектор круга с центральным углом 90 градусов составляет четвёртую часть от целого круга. Вообще, площадь сектора круга определяется по формуле:
Ответ: 0,25
27599. Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.
Площадь сектора круга определяется по формуле:
Длина дуги сектора:
Из этой формулы выражаем n и подставляем в формулу площади:
Подставляем:
Ответ: 1
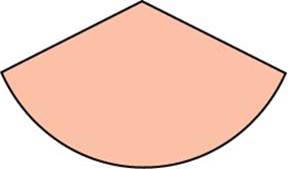
27600. Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.
Периметр прямоугольника равен сумме всех его сторон.
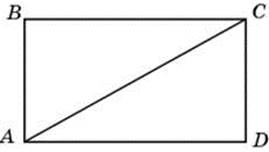
Используем стандартный приём, который применяется в подобных случаях. Пусть сторона ВС равна х, тогда АВ равна х+3. Противолежащие стороны в прямоугольнике равны, значит ВС=AD=х, AB=DC=х+3. Значит
Найдём площадь
Ответ: 18
27602. Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1: 2.
Площадь равна:
Соотношение соседних сторон равно 1 к 2, означает, что одна сторона в два раза больше другой. Обозначим BC за х, тогда AB будет равно 2х. Подставив в формулу периметра, эти значения найдём х.
Площадь равна:
Ответ: 18
27604. Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.
Обозначим AD=x, AB=y. Периметр равен:
Площадь равна:
Имеем два уравнения, можем составить систему:
Выразим, x во втором уравнении и подставим в первое:
Подставляем
Квадратное уравнение (общий вид):
Находим дискриминант Находим корни по формулам:
В нашем случае
Значит
Получили пару решений: AD=7, AB=14 и AD=14, AB=7, понятно, что большая сторона равна 14. Ответ: 14
27605. Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.
Для того, чтобы найти площадь, необходимо прямоугольника необходимо найти его стороны. Что мы можем выразить в этом прямоугольнике, используя данные нам величины и стороны. 1. Периметр равен:
2. По теореме Пифагора:
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

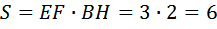

 раза, значит, площадь увеличилась в
раза, значит, площадь увеличилась в  раз. Значит, площадь большего многоугольника равна:
раз. Значит, площадь большего многоугольника равна: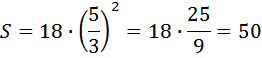
 .
.
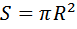
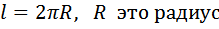

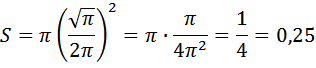
 . Найдите длину его окружности.
. Найдите длину его окружности.



 , центральный угол которого равен 90
, центральный угол которого равен 90 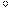 .
.








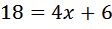
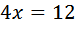


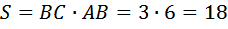

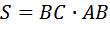





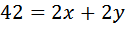
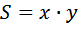
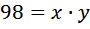
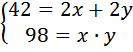
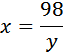
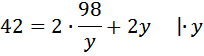



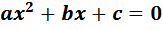
 .
.