
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное произведение векторов равно произведению модулей этих векторов на косинус угла между ними.
Модуль вектора равен его длине. Значит,
Ответ: 0 27711. Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину суммы векторов
Вектор
Ясно, что сумма векторов:
А длина вектора Ответ: 6
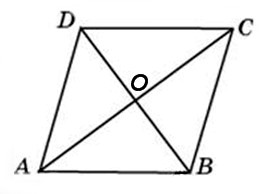
27713. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора
Свойств ромба: диагонали ромба пересекаются, и точкой пересечения делятся пополам; диагонали ромба пересекаются под прямым углом (90 градусов). В данной задаче необходимо найти длину АВ.
АВ является гипотенузой в прямоугольном треугольнике АОВ. По теореме Пифагора:
Длина вектора Ответ: 10
27715. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора
Свойств ромба: диагонали ромба пересекаются, и точкой пересечения делятся пополам; диагонали ромба пересекаются под прямым углом (90 градусов).
Длина вектора Ответ: 12
27716. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора
Свойств ромба: диагонали ромба пересекаются, и точкой пересечения делятся пополам; диагонали ромба пересекаются под прямым углом (90 градусов). Изобразим на эскизе разность векторов:
СВ является гипотенузой в прямоугольном треугольнике СОВ. По теореме Пифагора:
Длина вектора Ответ: 10
27719. Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите скалярное произведение векторов
Формула скалярного произведения векторов:
Скалярное произведение векторов равно произведению модулей этих векторов на косинус угла между ними.
Свойств ромба: диагонали ромба пересекаются, и точкой пересечения делятся пополам; диагонали ромба пересекаются под прямым углом (90 градусов). Значит:
Ответ: 0
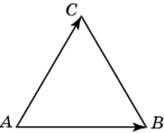
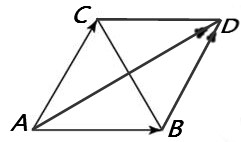
27720. Стороны правильного треугольника ABC равны
Сразу отметим, что в правильном треугольнике все углы равны 60 градусам. Используем правило параллелограмма. Достроим треугольник до параллелограмма.
Вектор Таким образом, нам необходимо найти длину Далее используем теорему косинусов:
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон умноженного на косинус угла между ними.
Нам известны АВ и BD, они равны
Длина вектора Ответ: 6
27722. Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов
Сразу отметим, что в правильном треугольнике все углы равны 60 градусам. Формула скалярного произведения векторов:
|
|||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.247.196 (0.011 с.) |

 и
и  .
.
 . Так как диагонали прямоугольника точкой пересечения делятся пополам, то есть их длины равны, и они одинаково направлены.
. Так как диагонали прямоугольника точкой пересечения делятся пополам, то есть их длины равны, и они одинаково направлены.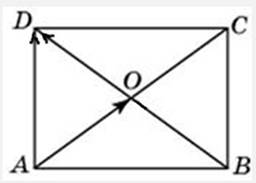

 равна шести.
равна шести. .
.


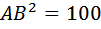





 это длина диагонали DB, равна 12.
это длина диагонали DB, равна 12. .
.










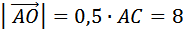



 . Найдите длину вектора
. Найдите длину вектора  .
.
 равен вектору
равен вектору  , значит
, значит  .
. .
.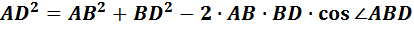
 . Значит,
. Значит,



 .
.




