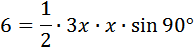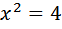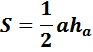Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Площадь параллелограмма равна произведению его стороны на высоту, опущенную на эту сторону.
В нашем случае мы можем записать:
Так как формулы выражают одну и ту же площадь, можем приравнять:
Ответ: 6
27612. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
Из рисунка видно, что большая высота это высота, опущенная на меньшую сторону. Обозначим точки пересечения высот со сторонами параллелограмма E и F.
Нам нужно найти DF. Запишем формулу площади параллелограмма:
Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
Из этой формулы мы можем найти угол С:
Заметьте, нам не нужно находить, чему равен сам угол, нам нужно именно значение синуса угла. Теперь рассмотрим прямоугольный треугольник FDC. Синус угла С в этом треугольнике равен:
Значит
Искомая высота равна 8. Как вы поняли во всех задачах, которые мы рассмотрели, используется две формулы для нахождения площади параллелограмма. Их нужно знать обязательно. Ответ: 8
27613. Найдите площадь ромба, если его высота равна 2, а острый угол 30
О ромбе мы знаем то, что его стороны равны. Построим высоту и обозначим её:
Имеем DE =2, угол А равен 30 градусам. Если мы найдём сторону ромба, то по формуле площади параллелограмма
сможем найти площадь ромба (ромб это параллелограмм, у которого все стороны равны). Рассмотрим прямоугольный треугольник ADE:
Теперь нам известно чему равны стороны ромба. Используем формулу для нахождения площади:
В нашем случае
Ответ: 8
27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
Для наглядности советуем изображать ромб именно так:
AC=12, площадь равна 18. Запомните ещё одну формулу для нахождения площади любого четырёхугольника:
Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними. В нашем случае
Вторая диагональ равна 3.
Ответ: 3 27616. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
Построим ромб так же, как в предыдущей задаче:
Известно, что Для нахождения
Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.
Получили, что меньшая диагональ равна 2. Ответ: 2
27619. Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.
Для нахождения площади воспользуемся формулой:
|
|||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.31.209 (0.011 с.) |


















 .
.












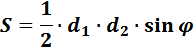






 . Обозначим
. Обозначим  .
. воспользуемся той же формулой:
воспользуемся той же формулой: