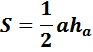Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное произведение векторов равно произведению модулей этих векторов и косинуса угла между ними. ⇐ ПредыдущаяСтр 4 из 4
Таким образом:
Ответ: 4,5
27723. Найдите сумму координат вектора
Координаты вектора определяются следующим образом: из соответствующих координат конца нужно вычесть координаты начала вектора, то есть если точки имеют координаты
Сумма координат равна 6+2= 8. Ответ: 8
27724. Вектор
Координаты вектора равны:
То есть Ответ: 8
27730. Найдите сумму координат вектора
Сначала необходимо определить координаты векторов Для того, чтобы найти координаты вектора, который является суммой других векторов, необходимо сложить соответствующие координаты этих векторов. Например, пусть
Сумма координат равна 10+10=20. Ответ: 20
27732. Найдите сумму координат вектора
Сначала нам необходимо определить координаты вектора
Сумма координат вектора Ответ: -4
27735. Найдите угол между векторами
Пусть вектор Для нахождения угла между векторами используем следующую формулу. Формула скалярного произведения векторов:
Также известна формула произведения векторов Значит,
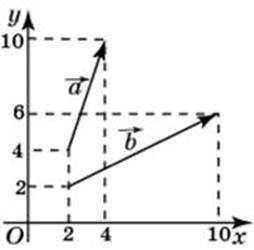
Координаты данных векторов равны
Угол между векторами равен 45 градусам, так как косинус 45 градусов равен Ответ: 45
27736. Найдите сумму координат вектора
Находим координаты вектора Находим координаты вектора Теперь найдём координаты вектора Сумма координат вектора Ответ: 20
27739. Найдите квадрат длины вектора
Находим координаты вектора Находим координаты вектора
Теперь найдём координаты вектора Длина вектора Квадрат длины равен 40. Ответ: 40
27741. Найдите угол между векторами
Пусть вектор Для нахождения угла между векторами используем следующую формулу. Формула скалярного произведения векторов:
Также известна формула произведения векторов Значит,
Находим координаты вектора Находим координаты вектора Координаты данных векторов равны Подставим их в формулу:
Угол между векторами равен 45 градусам, так как косинус 45 градусов равен Ответ: 45
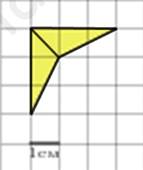
244995. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Используем следующий метод: разделим четырехугольник на два треугольника.
Площадь четырёхугольника равна сумме площадей полученных треугольников. Формула для нахождения площади треугольника:
|
|||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.236.219 (0.013 с.) |



 .
.
 , то вектор
, то вектор  . Найдём координаты вектора:
. Найдём координаты вектора:

 , где
, где 
 . Абсцисса точки В равна 8.
. Абсцисса точки В равна 8. .
.
 и
и  .
. , тогда
, тогда 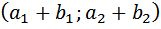 . Вектор
. Вектор  Значит, координаты вектора
Значит, координаты вектора 
 .
.

 .
.
 и
и 



 .
.

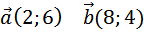 . Подставим их в формулу:
. Подставим их в формулу:
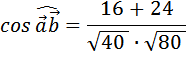


 .
.








 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.