Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условные графические обозначения в цепях постоянного иСодержание книги
Поиск на нашем сайте
Синусоидального токов. R
L
- конденсатор.

- источник синусоидальной ЭДС Е.
1.3. Требования к выполнению и оформлению расчетно-графических работ. Расчетно-графическая работа набирается на компьютере, шрифт №16, или, в крайнем случае, выполняется в отдельной тетради в клетку. Работы, написанные неразборчивым почерком, не принимаются. На титульном листе должны быть обозначены: Факультет, курс, № группы, фамилия, имя и отчество студента, фамилия, имя и отчество преподавателя, проверяющего работу, а также номер варианта задания. Номером варианта задания являются две последние цифры номера зачётной книжки или студенческого билета. На каждой странице должны быть оставлены поля шириной не менее 3 см. Электрические схемы должны быть вычерчены с соблюдением ГОСТ. Векторные диаграммы и графики строятся в масштабе с помощью чертежных инструментов. Оси координат вычерчивают сплошными тонкими линиями. Масштабы шкал по осям выбирают равномерными. Цифры шкал наносят слева от оси ординат и под осью абсцисс. Кривые на графике нумеруют. Надписи не должны выходить за пределы графика. Количество цифр в числах графика должно быть минимальным. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА. 2.1. Краткие теоретические сведения, методы и примеры расчета.
Рис.1. Рис.2. Закон Ома (Рис.1 и 2). Для пассивного участка цепи ab: Для активного участка цепи ab:
где: R – сопротивление участка цепи; Uab – напряжение на участке цепи; E –ЭДС источника и ток I, протекающий через участок цепи. Законы Кирхгофа (Рис.3). Узел - точка схемы, к которой присоединены три и более ветвей. Ветвь - это участок цепи между двумя узлами. Контур - любой замкнутый путь, по которому может течь электрический ток. На рисунке 3: A,B,C,D - узлы; AB,CD,BC,DA - ветви; ABCDA -контур. Закон Кирхгофа Алгебраическая сумма токов в узле электрической цепи равна нулю
Правило составления уравнений по I закону Кирхгофа Ток, который втекает в узел, имеет положительный знак, который вытекает, отрицательный. Пример: узел C 2 Закон Кирхгофа В замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения в данном контуре:
Правила составления уравнений по II закону Кирхгофа Когда направление обхода контура совпадает с направлением тока в сопротивлении, падение напряжения IR имеет знак +, если направления не совпадают, IR имеет отрицательный знак. Если направление обхода контура совпадает с направлением ЭДС, знак E положителен, если направления не совпадают - отрицателен. На пример, для контура ABCDA:
А I1 В E2 R4 I4 I2 R2 I3 E3 D C I9 R3 I8 I7 Рис.3. Баланс мощностей. В любом замкнутом контуре суммарная мощность, выделяемая источниками ЭДС
где: При этом в генераторном режиме источника направления ЭДС Еi и тока Ii совпадают по знаку, а в режиме потребителя они противоположны. Для контура ABCDA:
Последовательное соединение резисторов (Рис. 4).
U U1 U2 R2 U3 R3 Рис. 4. В этом случае единственный ток I протекает через все резисторы По второму закону Кирхгофаимеем:
откуда и наконец Для n последовательно включенных сопротивлений:
Параллельное соединение резисторов (Рис.5). Единственное напряжение U приложено ко всем сопротивлениям Согласно первому закону Кирхгофаимеем:
откуда
Рис. 5. Проводимость - величина, обратная сопротивлению: G = 1/Ом. Тогда для n включённых параллельно сопротивлений:
Частный случай: Если имеем только два включённых параллельно сопротивленияR1 и R2, то эквивалентное сопротивление цепи равно:
откуда
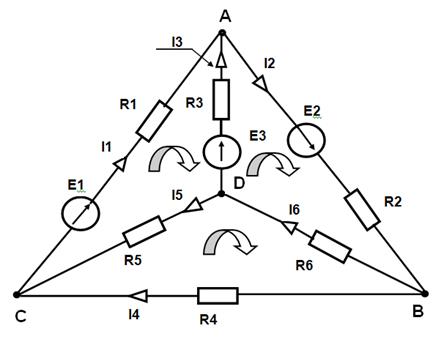
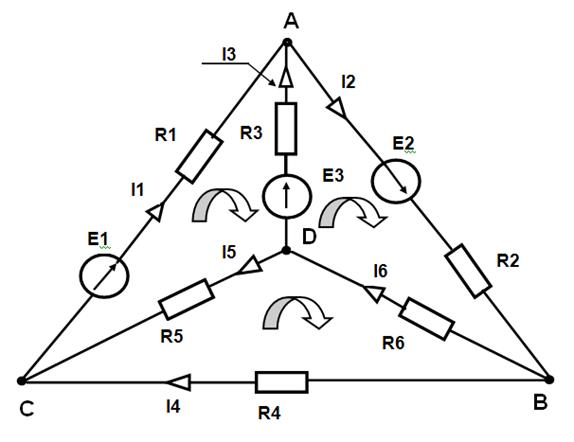
Примеры решения задач Метод законов Кирхгофа Пример №1. Для электрической цепи, схема которой изображена на рис.1.1 по заданным сопротивлениям и ЭДС выполнить следующее: 1. Составить систему уравнений для определения токов по первому и второму законам Кирхгофа, для чего необходимо: 1.1. Определить число ветвей, а по ним - число неизвестных токов (m). Этим числом определяется общее количество уравнений, составленных по первому и второму законам Кирхгофа. 1.2. Произвольно выбрать положительные направления токов I 1, I 2 и т.д. 1.3. Определить количество уравнений y, которые следует составить по пер-
вому закону Кирхгофа у = п - 1, где n - количество узловых точек (узлов). Пример: п = 4, у = 4 - 1 = 3 уравнения. 1.4. Составить у уравнений по первому закону Кирхгофа. При этом условимся с плюсом записывать токи, идущие к узлу, а токи, направленные от него – с минусом. 1.5. Определить количество уравнений k, которые следует составить по вто- рому закону Кирхгофа k = т - (п - 1 ), где т - общее число всех неиз- вестных токов. Пусть т = 6, п = 4, тогда k = 6 - (4 -1) = 3 уравнения. 1.6. Произвольно выбрать независимые контуры и направление обхода в них. 1.7. Составить для независимых контуров «k» уравнений по второму закону Кирхгофа. Условимся, что если ЭДС, напряжения и токи совпадают с направлением выбранного обхода контура, то им приписывают знак «плюс», а если не совпадают - «минус». Запишем систему т уравнений, составленную для данного примера из 3х уравнений по первому и 3х уравнений по второму закону Кирхгофа. Уравнения записываем в регулярной форме. 1.8. Составить определители из коэффициентов токов и значений Э,Д,С, 1.9. Загрузить в оперативную память компьютера программу решения системы т уравнений. 1.10. Ввести коэффициенты в компьютер. 1.11. Сделать распечатку. Рассмотрим электрическую цепь Рис.1.1.: E 1 =22В, E 2 = 24 B, E з=10В
R 01 =0,2Ом R 02= 0 Ом Рис.1.1. R оз =1,2Ом R 1 =2 Ом R 2 =1 Ом R з=8 Ом R 4=4 Ом R 5 = 10 Ом R 6 =6 Ом Определить токи в ветвях, пользуясь законами Кирхгофа. Решение 1.1. Определяем число ветвей, а по ним - число неизвестных токов (m). m = 6. 1.2. Произвольно выбираем положительные направления токов I 1, I 2 и т.д. (см. рис. 1). 1.3. Определяем количество уравнений у, которые следует составить по пер вому закону Кирхгофа: у = n - 1, где n - количество узловых точек (узлов). п = 4, у = 4 – 1 = 3 уравнения. 1.4. Составляем у уравнений по первому закону Кирхгофа. Токи, идущие к узлу, записываем с плюсом, а токи, направленные от него - с минусом. Для узла А: I 1 - I 2 + I 3 = 0 Для узла В: I 2 – I 4 – I 6 = 0 Для узла D: - I з – I 5 + I 6 = 0 1.5. Установим количество уравнений k, которые следует составить по втоpому закoну Kирхгофа: k = m - (n - 1), где m - общее число всех неизвестных токов. т = 6, n = 4, тогда k = 6- (4 - 1) = 3 уравнения. 1.6. Выберем произвольно независимые контуры и положительные направления обхода в них (см. рис. 1). Поэтому если ЭДС, напряжения и токи совпадают с направлением обхода контура, им приписываем знак «плюс», а если не совпадают - «минус». 1.7. Составляем для независимых контуров «k» уравнений по второму закону Kирхгофа: Для контура I: (R1 + R01)* I1 - (R3 + Rо3)* I3 + R5 * I5 = E1 – Е3 Для контура 2: (R3 + R02)* I2 + (R3 + Rо3)* I3 + R6* I6 = E2 + Е3 Для контура 3: R4 * I4 –R5 * I5 – R6* I6 = 0 Запишем систему из т уравнений, в которую входят уравнения, составлен- ные по первому и второму закону Кирхгофа. Систему уравнений записываем в регулярной форме. I1 - I2 + Iз + 0 + 0 + 0 = 0 0 + I2 + 0 - I4 + 0 - I6 = 0 0 + 0 - Iз + 0 - I5 + I6 = 0 (R1+Rо1)*I1 + 0 - (Rз+Rоз)*I3 + 0 + R5*I5 + 0 = Е1 - Ез 0 + (R2+R02)*I2+ (Rз+Rоз)*Iз + 0 + 0 + R6*I6 = E2+E3 0 +0 + 0 + R4 * I4 - R5 * I5 + R6* I6 = 0 1.8. Составим определители из коэффициентов токов и значений ЭДС.
0 + 1 + 0 - 1 + 0 - 1 = 0 0 + 0 - 1 + 0 - 1 + 1 = 0 2.2 + 0 - 9.2 + 0 + 10 + 0 = 12 0 + 1 + 9.2 + 0 + 0 + 6 = 34 0 + 0 + 0 + 4 - 10 - 6 = 0
1.9. Загрузим в оперативную память компьютера программу решения системы т уравнений. 1.10. Введем коэффициенты в компьютер. 1.11. Распечатаем результат. Метод контурных токов Для уменьшения количества уравнений применяют метод контурных токов. Составляются уравнения только по второму закону Кирхгофа для
независимых контуров. Во внешних ветвях контура реальные токи и контурные токи равны по абсолютной величине. Во внутренних (смежных) ветвях реальные токи равны алгебраической сумме контурных токов, проходящих по этим ветвям. Пример№2: рассмотрим ту же электрическую цепь и те же значения для ЭДС и сопротивлений. E 1 = 22 В, E 2 = 24 B, Eз = 10 В, R 01 = 0,2Ом R 02= 0 Ом R оз = 1,2Ом R 1 = 2 Ом R 2 = 1 Ом Rз= 8 Ом R4= 4 Ом R5 = 10 Ом R6 = 6 Ом Определить токи в ветвях схемы Рис.1.3 методом контурных токов
Рис. 1.3. Решение: Составим уравнения по второму закону Кирхгофа для независимых контуров (R1+Rо1+Rз+Rоз+R5)* I1k - (Rз+Rоз)* I2k - R5* I3k =Е1-Ез - (Rз+Rоз)* I1k +(R 2 +Rо 2 +Rз+Rоз+R 6)* I2k –R 6 * I3k = E 2 +Ез - R 5 * I1k - R 6 * I2k + (R 4 +R 5 +R 6)* I3k = 0 Подставим числовые значения сопротивлений и ЭДС и представим в виде определителя:
Введем числовые данные определителя в компьютер и сделаем распечатку контурных токов: I1k = 6,729 А I2k = 8,06 А I3k = 5,783 А Определим реальные токи в ветвях: I1 = I2k = 6, 729 А I2 = I2k = 8, 062 А I3 = I2k – I1k = 8,062 А - 6,729 А = 1,333 А I4 = I3k = 5,783 А I5 = I1k – I3k = 6,729 А - 5,783 А = 0,945 А. I6 = I2k – I3k = 8,062 А - 5, 783 А = 2,278 А Метод узловых потенциалов М.У.П. Метод узловых потенциалов М.У.П. основан на первом законе Кирхгофа и позволяет сократить количество уравнений для сложной электрической цепи. Пример №3: Рассчитать токи методом узловых потенциалов в схеме Рис. 1.4.
1. Заземлим точку D Рис.1.4. 2. Обозначим потенциал точки А через φ а, а потенциал точки В через φ в, потенциал точки С через φ с.
3. ИСХОДНЫЕ ДАННЫЕ: Е1 = 22 В; Е 2 = 24 В; Е з = 10 В. R01 = 0,2 Ом; Ro2 = 0; Rоз = 1,2Oм R1 = 2 Ом;R 2 = 1 Ом; Rз = 8 Ом. R4 = 4 Ом; R5=10 Ом; R 6 =6Ом Определить токи в ветвях.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.106.87 (0.01 с.) |




 - резистор
- резистор - катушка индуктивности.
- катушка индуктивности. C
C Е
Е

 - источник постоянной ЭДС Е;
- источник постоянной ЭДС Е; Основные законы и расчетные формулы.
Основные законы и расчетные формулы.

 ,
, .
.


 I5 E1 R1 I6
I5 E1 R1 I6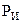 равна мощности, преобразуемой в другие виды энергии потребителями
равна мощности, преобразуемой в другие виды энергии потребителями  , т.е.
, т.е. ,
, и
и  .
.
 I R1
I R1 .
. ,
,
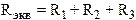 (эквивалентное сопротивление).
(эквивалентное сопротивление). .
. ,
, .
.
 .
.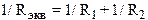 ,
, .
.