
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принятые буквенные обозначения основных электрических величинСодержание книги
Поиск на нашем сайте
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ Принятые буквенные обозначения основных электрических величин u, e, i, p -мгновенные значения напряжения, ЭДС, тока и мощности; U, E, I - постоянные или действующие значения напряжения, ЭДС и тока; Um, Em, Im - амплитудные значения напряжения, ЭДС и тока; P,Q,S - активная, реактивная и полная мощности; R, X, Z - активное, реактивное и полное сопротивления; G, B, Y - активная, реактивная и полная проводимости;
yu,yi, - начальные фазы напряжения и тока; j - разность фаз; f, w, T - частота, угловая частота, период.
Условные графические обозначения в цепях постоянного и Синусоидального токов. R
L
- конденсатор.

- источник синусоидальной ЭДС Е.
1.3. Требования к выполнению и оформлению расчетно-графических работ. Расчетно-графическая работа набирается на компьютере, шрифт №16, или, в крайнем случае, выполняется в отдельной тетради в клетку. Работы, написанные неразборчивым почерком, не принимаются. На титульном листе должны быть обозначены: Факультет, курс, № группы, фамилия, имя и отчество студента, фамилия, имя и отчество преподавателя, проверяющего работу, а также номер варианта задания. Номером варианта задания являются две последние цифры номера зачётной книжки или студенческого билета. На каждой странице должны быть оставлены поля шириной не менее 3 см. Электрические схемы должны быть вычерчены с соблюдением ГОСТ. Векторные диаграммы и графики строятся в масштабе с помощью чертежных инструментов. Оси координат вычерчивают сплошными тонкими линиями. Масштабы шкал по осям выбирают равномерными. Цифры шкал наносят слева от оси ординат и под осью абсцисс. Кривые на графике нумеруют. Надписи не должны выходить за пределы графика. Количество цифр в числах графика должно быть минимальным. Закон Кирхгофа Алгебраическая сумма токов в узле электрической цепи равна нулю
Правило составления уравнений по I закону Кирхгофа
Ток, который втекает в узел, имеет положительный знак, который вытекает, отрицательный. Пример: узел C 2 Закон Кирхгофа В замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения в данном контуре: Правила составления уравнений по II закону Кирхгофа Когда направление обхода контура совпадает с направлением тока в сопротивлении, падение напряжения IR имеет знак +, если направления не совпадают, IR имеет отрицательный знак. Если направление обхода контура совпадает с направлением ЭДС, знак E положителен, если направления не совпадают - отрицателен. На пример, для контура ABCDA:
А I1 В E2 R4 I4 I2 R2 I3 E3 D C I9 R3 I8 I7 Рис.3. Баланс мощностей. В любом замкнутом контуре суммарная мощность, выделяемая источниками ЭДС
где: При этом в генераторном режиме источника направления ЭДС Еi и тока Ii совпадают по знаку, а в режиме потребителя они противоположны. Для контура ABCDA:
Последовательное соединение резисторов (Рис. 4).
U U1 U2 R2 U3 R3 Рис. 4. В этом случае единственный ток I протекает через все резисторы По второму закону Кирхгофаимеем:
откуда и наконец Для n последовательно включенных сопротивлений:
Параллельное соединение резисторов (Рис.5). Единственное напряжение U приложено ко всем сопротивлениям Согласно первому закону Кирхгофаимеем:
откуда
Рис. 5. Проводимость - величина, обратная сопротивлению: G = 1/Ом. Тогда для n включённых параллельно сопротивлений:
Частный случай: Если имеем только два включённых параллельно сопротивленияR1 и R2, то эквивалентное сопротивление цепи равно:
откуда
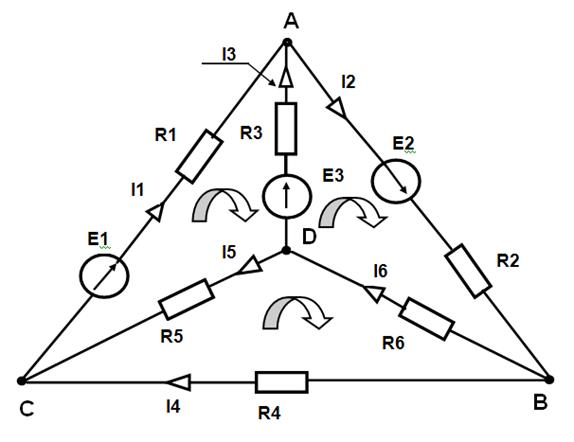
Примеры решения задач Метод законов Кирхгофа Пример №1. Для электрической цепи, схема которой изображена на рис.1.1 по заданным сопротивлениям и ЭДС выполнить следующее: 1. Составить систему уравнений для определения токов по первому и второму законам Кирхгофа, для чего необходимо: 1.1. Определить число ветвей, а по ним - число неизвестных токов (m). Этим числом определяется общее количество уравнений, составленных по первому и второму законам Кирхгофа.
1.2. Произвольно выбрать положительные направления токов I 1, I 2 и т.д. 1.3. Определить количество уравнений y, которые следует составить по пер- вому закону Кирхгофа у = п - 1, где n - количество узловых точек (узлов). Пример: п = 4, у = 4 - 1 = 3 уравнения. 1.4. Составить у уравнений по первому закону Кирхгофа. При этом условимся с плюсом записывать токи, идущие к узлу, а токи, направленные от него – с минусом. 1.5. Определить количество уравнений k, которые следует составить по вто- рому закону Кирхгофа k = т - (п - 1 ), где т - общее число всех неиз- вестных токов. Пусть т = 6, п = 4, тогда k = 6 - (4 -1) = 3 уравнения. 1.6. Произвольно выбрать независимые контуры и направление обхода в них. 1.7. Составить для независимых контуров «k» уравнений по второму закону Кирхгофа. Условимся, что если ЭДС, напряжения и токи совпадают с направлением выбранного обхода контура, то им приписывают знак «плюс», а если не совпадают - «минус». Запишем систему т уравнений, составленную для данного примера из 3х уравнений по первому и 3х уравнений по второму закону Кирхгофа. Уравнения записываем в регулярной форме. 1.8. Составить определители из коэффициентов токов и значений Э,Д,С, 1.9. Загрузить в оперативную память компьютера программу решения системы т уравнений. 1.10. Ввести коэффициенты в компьютер. 1.11. Сделать распечатку. Рассмотрим электрическую цепь Рис.1.1.: E 1 =22В, E 2 = 24 B, E з=10В
R 01 =0,2Ом R 02= 0 Ом Рис.1.1. R оз =1,2Ом R 1 =2 Ом R 2 =1 Ом R з=8 Ом R 4=4 Ом R 5 = 10 Ом R 6 =6 Ом Определить токи в ветвях, пользуясь законами Кирхгофа. Решение 1.1. Определяем число ветвей, а по ним - число неизвестных токов (m). m = 6. 1.2. Произвольно выбираем положительные направления токов I 1, I 2 и т.д. (см. рис. 1). 1.3. Определяем количество уравнений у, которые следует составить по пер вому закону Кирхгофа: у = n - 1, где n - количество узловых точек (узлов). п = 4, у = 4 – 1 = 3 уравнения. 1.4. Составляем у уравнений по первому закону Кирхгофа. Токи, идущие к узлу, записываем с плюсом, а токи, направленные от него - с минусом. Для узла А: I 1 - I 2 + I 3 = 0 Для узла В: I 2 – I 4 – I 6 = 0 Для узла D: - I з – I 5 + I 6 = 0 1.5. Установим количество уравнений k, которые следует составить по втоpому закoну Kирхгофа: k = m - (n - 1), где m - общее число всех неизвестных токов. т = 6, n = 4, тогда k = 6- (4 - 1) = 3 уравнения. 1.6. Выберем произвольно независимые контуры и положительные направления обхода в них (см. рис. 1). Поэтому если ЭДС, напряжения и токи совпадают с направлением обхода контура, им приписываем знак «плюс», а если не совпадают - «минус». 1.7. Составляем для независимых контуров «k» уравнений по второму закону Kирхгофа: Для контура I: (R1 + R01)* I1 - (R3 + Rо3)* I3 + R5 * I5 = E1 – Е3 Для контура 2: (R3 + R02)* I2 + (R3 + Rо3)* I3 + R6* I6 = E2 + Е3 Для контура 3: R4 * I4 –R5 * I5 – R6* I6 = 0 Запишем систему из т уравнений, в которую входят уравнения, составлен- ные по первому и второму закону Кирхгофа. Систему уравнений записываем в регулярной форме. I1 - I2 + Iз + 0 + 0 + 0 = 0 0 + I2 + 0 - I4 + 0 - I6 = 0 0 + 0 - Iз + 0 - I5 + I6 = 0 (R1+Rо1)*I1 + 0 - (Rз+Rоз)*I3 + 0 + R5*I5 + 0 = Е1 - Ез 0 + (R2+R02)*I2+ (Rз+Rоз)*Iз + 0 + 0 + R6*I6 = E2+E3 0 +0 + 0 + R4 * I4 - R5 * I5 + R6* I6 = 0 1.8. Составим определители из коэффициентов токов и значений ЭДС.
0 + 1 + 0 - 1 + 0 - 1 = 0 0 + 0 - 1 + 0 - 1 + 1 = 0 2.2 + 0 - 9.2 + 0 + 10 + 0 = 12 0 + 1 + 9.2 + 0 + 0 + 6 = 34 0 + 0 + 0 + 4 - 10 - 6 = 0
1.9. Загрузим в оперативную память компьютера программу решения системы т уравнений. 1.10. Введем коэффициенты в компьютер. 1.11. Распечатаем результат.
Метод контурных токов Для уменьшения количества уравнений применяют метод контурных токов. Составляются уравнения только по второму закону Кирхгофа для независимых контуров. Во внешних ветвях контура реальные токи и контурные токи равны по абсолютной величине. Во внутренних (смежных) ветвях реальные токи равны алгебраической сумме контурных токов, проходящих по этим ветвям. Пример№2: рассмотрим ту же электрическую цепь и те же значения для ЭДС и сопротивлений. E 1 = 22 В, E 2 = 24 B, Eз = 10 В, R 01 = 0,2Ом R 02= 0 Ом R оз = 1,2Ом R 1 = 2 Ом R 2 = 1 Ом Rз= 8 Ом R4= 4 Ом R5 = 10 Ом R6 = 6 Ом Определить токи в ветвях схемы Рис.1.3 методом контурных токов
Рис. 1.3. Решение: Составим уравнения по второму закону Кирхгофа для независимых контуров (R1+Rо1+Rз+Rоз+R5)* I1k - (Rз+Rоз)* I2k - R5* I3k =Е1-Ез - (Rз+Rоз)* I1k +(R 2 +Rо 2 +Rз+Rоз+R 6)* I2k –R 6 * I3k = E 2 +Ез - R 5 * I1k - R 6 * I2k + (R 4 +R 5 +R 6)* I3k = 0 Подставим числовые значения сопротивлений и ЭДС и представим в виде определителя:
Введем числовые данные определителя в компьютер и сделаем распечатку контурных токов: I1k = 6,729 А I2k = 8,06 А I3k = 5,783 А Определим реальные токи в ветвях: I1 = I2k = 6, 729 А I2 = I2k = 8, 062 А I3 = I2k – I1k = 8,062 А - 6,729 А = 1,333 А I4 = I3k = 5,783 А I5 = I1k – I3k = 6,729 А - 5,783 А = 0,945 А. I6 = I2k – I3k = 8,062 А - 5, 783 А = 2,278 А Метод узловых потенциалов М.У.П. Метод узловых потенциалов М.У.П. основан на первом законе Кирхгофа и позволяет сократить количество уравнений для сложной электрической цепи. Пример №3: Рассчитать токи методом узловых потенциалов в схеме Рис. 1.4.
1. Заземлим точку D Рис.1.4. 2. Обозначим потенциал точки А через φ а, а потенциал точки В через φ в, потенциал точки С через φ с.
3. ИСХОДНЫЕ ДАННЫЕ: Е1 = 22 В; Е 2 = 24 В; Е з = 10 В. R01 = 0,2 Ом; Ro2 = 0; Rоз = 1,2Oм R1 = 2 Ом;R 2 = 1 Ом; Rз = 8 Ом. R4 = 4 Ом; R5=10 Ом; R 6 =6Ом Определить токи в ветвях. Узловых потенциалов. Д ЛЯ узла А: φ А * g 11 - φ В* g 12 - φ С* g 13 = Е1 g1 1 + E3 g1 3 - E2 g12 Д ЛЯ узла В: - φ А*g21+ φ В*g22 - φ С * g 23 = E2 g 2 Д ЛЯ узла С: - φ А * g31 - φ В* g32 + φ С* g33 = - Е1 g 1 Где: g11 =(g 1+g 2 +g 3) = 0,454 +1 +0,108 = 1,563 g 1 = 1/(R1+Rо1) = 1/(2+0,2) = 0,454; g2 = 1 / R2 = 1/1=1; gз = 1 / (Rз + Rоз) = 1 / (8 + 1,2) = 0,108; g12 = g21 = g 2 = g2 = 1/R2 = 1/1= 1; g13 = g 31 = g 1 = 0,454; g23= g32 = g4 = 1/R4 = 1/4 = 0,25; g22 = (g2+g4+g6) = (1/R2+1/R4+1/R6) = = (1+ 0,25+0,166) =1,416; g6= 1/R6=1/6= 0,166 g 33 = (g1 + g 4 + g 5) = (1 / R1 + 1 / R4 + 1 / R5) = (0,454 + 0,25 + 0,1) = =0,804; g5 =1/R5= 1 /10 =0,1. Составим из проводимостей определитель:
-g21 + g22 - g23 Е2 g2 -g31 - g32 + g33 -E1 g 11
Подставим численные значения:
-1 +1,416 - 0,25 24 - 0,454 - 0,25 + 0,804 -10 Введем в компьютер, получим: φ а = - 2, 263 В; φ в = 13, 673 В; φ с = - 9,459 В;
Определим токи в ветвях: I 1 = (E1 +φс - φ а) / (R1 + R01) = (22 +(- 9, 459) + 2, 263) / 2,2 = 6,729 А I 2 =(E2 + φ а - φв) / (R2) = (24 +(- 2,263) - 13,673) /1= 8, 062 А I з = (Ез - φ а) / (Rз + Rоз) = (10 - 2,263) / (8+1,2) = 1,333 А I 4 = (φ в - φ с) / (R4) = (13,673 + 9,459) /4 = 5,783 А I 5 = (φ с) / (R5) = (- 9,459) /10 = - 0,915 А I 6 = (φ в)/(R6) = (13,673) /6 = 2,278 А
Короткого замыкания) Его применяют, когда требуется определить ток в одной ветви. Порядок расчета: 1. Разрывают ветвь, в которой требуется определить ток. 2. Любым методом определяют Uxx = Ег (чаще МКТ). 3. Для определения тока короткого замыкания эту ветвь замыкают накоротко.
Пример №4: Рис.1.5. ИСХОДНЫЕ ДАННЫЕ: Е1 = 22В; Е2 = 24В; Е3 = 10 В. Rо 1 = 0,2 Ом; Rо2 = 0; Rоз = 1,2 Ом;
R1 = 2 Ом; R 2 = 1 Ом; Rз = 8 Ом; R4 = 4 Ом; R 5 = 10 Ом; R 6 = 6 Ом; Определить ток в ветви ВD (Рис. 1.6) методом эквивалентного генератора. Замечание: в дальнейшем для удобства будем обозначать: R 11 = R1+Rо1, аR 13 = R3+Ro3. Холостой ход (Рис. 1.7) А
1. Заземлим точку С. Рис. 1.7. 2. Удалим R 6. 3. Обозначим потенциал точки В через φв, потенциал точки D через φd. 4. Для определения Uвd = Uхх = Eг необходимо составить два уравнения для двух контуров САDС и АВСDА по второму закону Кирхгофа. 5. Обозначим направления обхода контуров и составим уравнения по методу контурных токов: I1к(R11 + R1з + R5) – I2к (R13 + R5) = E1 - Ез - I1к (R1з + R5) + I2к (R2 + R4 + R1 3 + R5) = Е2 + Е3 6. Из коэффициентов составим определитель:
-(R1з + R5) + (R2 + R 4 + R13 + R5) Е2 + Е3
21,4 - 19,2 12 - 19,2 24,2 34 7. Введем в компьютер числовые значения определителя, получим: I1к = 6,32 I2к = 6,419 8. Определим реальные токи: I 2 = I 2 к = 6,419 А; I 5 = I 1 к - I 2 к = 6,419 А. 9. Определим потенциалы φ в и φ d: φ в = I2*R4 = 6,419*4 = 25,676 В φ d = I5 * R5 = - 0,99В. 10.Определим Е г = U хх = Uвd = φ в - φ d = 25,676 - (- 0,99)= = 26,668 В Определение тока короткого замыкания I кз методом контурных токов 1. Для определения короткого замыкания I кз необходимо замкнуть точки В и D проводником и составить три уравнения для контурных токов (Рис. 1.8).
I1к* (R 11 +R 13 + R5) – I 2 к*R 13 - I 3 к*R5 = Е1 – Ез I1к*R 13 + I 2 к*R2+ R1 3) - I 3 к*(0) = Е 2 +Ез -I1к*R 5 - I 2 к*(0) + Iзк*(R4 +R 5) = 0 2. Из коэффициентов составим определитель:
- (R 13) + (R2+ R 13) - (0) Е2 + Ез - (R5) - (0) + (R4 +R5) 0
или:
-9,2 +10,2 0 34 -10 0 +14 14
3. Введем в компьютер числовые значения определителя, получим I 1 к = 7,159 I 2 к =9, 791 I 3 к = 5,114 4. Oпределим ток короткого замыкания Iк.з. = I 2 к – I3к = 4,677 А 5. Определим внутреннее сопротивление генератора: Rг = Rвн = Ег / Iкор.зам. = 26,668/4,677 = 5, 701 Ом. 6. Определим ток I 6 I6 = Ег/(Rг+R6) = 26, 668 / (5, 701 + 6) = 2,278 А
Баланс мощностей ΣIЕ = Σ I2R ΣIЕ = I 1 * Е 1 + I 2 * Е2 + Iз* Ез = 6,729* 22 + 8, 062*24+ 1,333*10 = 354, 86 Вт. ΣI²R = I 21 *R1 1 + I ²2 R2 + I 2 з*R1з + I 2 4 *R 4 + I²5R5 + I2 6 R6 = 6.729 2 *2,2 + + 8, 062 2 * 1 + 1,333 2 * 9,2 + 5, 783 ²* 4 + 0, 945 2 *10 + 2,278 2 *6 = 99, 622 + 65 + 16, 348 + 133, 787 +8, 948 +31,162 = 354,86 Вт
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ Примеры решения задач Пример №1. 1. Определить токи в ветвях цепи и напряжения на отдельных участках схемы Рис. 3.5.
2. Составить баланс активной и реактивной мощностей. 3. Построить в масштабе на комплексной плоскости векторную диаграмму токов и потенциальную диаграмму напряжений по внешнему контуру.
Рис.3.5. Решение:
Xc1 = 1/2π fC1 = 1 /2π *50 * 637* X L3 = 2πfL3 = 2π *50 *15,9 *10 3 = 4, 995 om. 2. Oпpeдeляeм комплексныe coпpотивления: Z 1 = R 1 - j Xc 1 = 2 - j 4, 997 =5,381 * е j68. Ом; Z 2 = R 2 = 3 Oм.;
Z 23 =(Z 2 *Z 3)/(Z 2 +Z 3)=(3*6,399* e j51)/(3+4+ j 4,995)= = (3 * 6, 399 * 6 е –j51) / 8, 599* e j3 5, 5 = 2,232 * e j 15. 8 = 2,148 + j 0,607 Оm. Zэ = (Z 1 + Z 23) = (2 - j 4, 997) + (2, 148 + j 0,607) = 4,148 - j 4,389 =
3. Опpeделяeм ток I1:
U 1 = I 1 *Z 1 = 24,838 e j46 * 5,381 e j68= 133,653 * e -j21. =124,3 - j 49,116 B
I3=U AB /Zз = 55,433 * е j62. / 6, 399 * e j51 = 8, 662 * e j11 = 8,5 + j 1,662 А 6. Проведем проверку решения:
= 17,066 + j18,034 А.
I 1 =24, 838 * е j46 ; I 2 = 18, 477 * е j62 ; I3 = 8, 662 * e j11
Рис.3.6. Данные для векторной диаграммы напряжений Рис.3.7.
UС 1= I 1 * ZС1=24,838 e j46 *5 e -j90 =124 e–j44В.
U L3= I 3 * Z L 3=8, 662 * e j11*5 e j90 = 43,5 e j101В;
Рис.3.7. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ К экзамену или зачёту. Источники постоянного напряжения и тока. Определения, характеристики, область применения. Расчет электрических цепей методом свертывания. Входное сопротивление. Расчет электрических цепей методом законов Кирхгофа. Расчет электрических цепей методом наложения. Расчет эл. цепей методом контурных токов. Расчет электрических цепей методом узловых потенциалов. Графический метод расчета нелинейных цепей постоянного тока, статическое и дифференциальное сопротивления. Построение потенциальных диаграмм в электрических цепях. Изображение синусоидальных функций времени на комплексной плоскости. Активное сопротивление, индуктивность и емкость в цепи синусоидального тока. Векторные диаграммы. Резонанс токов. Резонанс напряжений. Работа трехфазной системы при соединении нагрузки звездой с нулевым проводом. Соотношения между фазными и линейными напряжениями и токами в трехфазной системе при соединении симметричной нагрузки звездой без нулевого провода. Работа трехфазной системы при соединении нагрузки треугольником. Соотношения между фазными и линейными напряжениями и токами. Мощность в цепи трехфазного синусоидального тока. Способы повышения cos φ. Принцип действия однофазного трансформатора, энергетическая диаграмма. Однофазный трансформатор. Схема замещения. Основные уравнения. Векторная диаграмма. Опыт холостого хода однофазного трансформатора, определяемые параметры. Опыт короткого замыкания однофазного трансформатора, определяемые параметры. Трансформаторы напряжения и тока. Трехфазный трансформатор. Назначение, принцип работы. Схемы соединения, группы соединения. Принцип действия двигателя постоянного тока. Работа электрической машины постоянного тока в режиме двигателя. Способы пуска и регулирования скорости двигателей постоянного тока. Механические характеристики электродвигателей постоянного тока. Генератор постоянного тока с самовозбуждением, условия самовозбуждения. Принцип действия трехфазного асинхронного двигателя, способы пуска. Трехфазный асинхронный двигатель. Скольжение. Работа в режиме торможения. Трехфазный асинхронный двигатель. Механические характеристики. Двигатель с фазным ротором. Полупроводниковый диод. Принцип действия. Вольтамперная характеристика, схема однополупериодного выпрямления. Полупроводниковый диод. Принцип действия, вольтамперная характеристика, схема двухполупериодного выпрямления. Трехфазное выпрямление переменного тока. Стабилитроны. Особенности работы, вольтамперные характеристики, схемы включения. Параметрический стабилизатор. Транзисторный усилитель. Основные схемы включения транзистора. Амплитудно-частотная характеристика однокаскадного транзисторного усилителя. Работа транзистора в ключевом режиме. Операционные усилители. Принцип действия, основные уравнения, схемы включения, параметры. Цифровые микросхемы. Принцип действия, применение, реализуемые логические функции.
Задания для контрольной работы по расчёту цепей постоянного тока, однофазного синусоидального тока и трёхфазных цепей.
Задача 1. Для электрической цепи, схема которой изображена на рис. 1.1 – 1.100 по данным в табл. 1 сопротивлениям и ЭДС выполнить следующее: 1. Составить и решить систему уравнений, необходимых для определения токов по первому и второму закону Кирхгофа; 2. Найти все токи, пользуясь методом контурных токов; 3. Проверить правильность решения, применив метод узловых потенциалов; 4. Определить ток в резисторе R6 методом эквивалентного генератора; 5. Определить показания вольтметра и составить баланс мощностей для заданной схемы; 6. Построить в масштабе потенциальную диаграмму для внешнего контура. Табл. 1
|


 - комплексы действующих значений напряжения, ЭДС и тока;
- комплексы действующих значений напряжения, ЭДС и тока; - комплексы амплитудных значений напряжения, ЭДС и тока;
- комплексы амплитудных значений напряжения, ЭДС и тока; - комплексы реактивной и полной мощности;
- комплексы реактивной и полной мощности; - комплексы полного сопротивления и проводимости;
- комплексы полного сопротивления и проводимости;


 - резистор
- резистор - катушка индуктивности.
- катушка индуктивности. C
C Е
Е

 - источник постоянной ЭДС Е;
- источник постоянной ЭДС Е; .
.


 I5 E1 R1 I6
I5 E1 R1 I6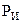 равна мощности, преобразуемой в другие виды энергии потребителями
равна мощности, преобразуемой в другие виды энергии потребителями  , т.е.
, т.е. ,
, и
и  .
.
 I R1
I R1 .
. ,
,
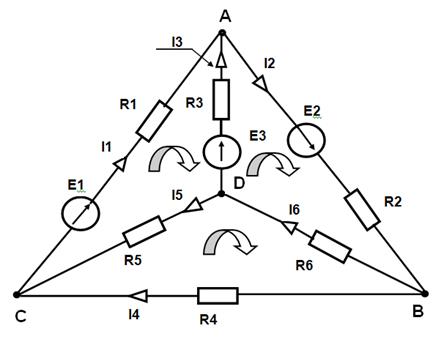
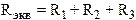 (эквивалентное сопротивление).
(эквивалентное сопротивление). .
. ,
, .
.
 .
.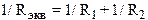 ,
, .
.





 g11 - g12 - g1з E1 g13 + Ез g13 – Е2 g12
g11 - g12 - g1з E1 g13 + Ез g13 – Е2 g12


 1,563 - 1 -0,454 -12. 913
1,563 - 1 -0,454 -12. 913 4. Зная U xx и ток короткого замыкания Iкз, определяют внутреннее сопротивление генератора Rвн = U xx / Iкз. 5.Затем определяют искомый ток в ветви, например I6: I 6 =Ег/(Rвн+R 6)
4. Зная U xx и ток короткого замыкания Iкз, определяют внутреннее сопротивление генератора Rвн = U xx / Iкз. 5.Затем определяют искомый ток в ветви, например I6: I 6 =Ег/(Rвн+R 6) Рис.1.6.
Рис.1.6.



 Подставим числовые значения
Подставим числовые значения

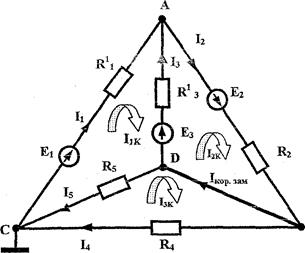 в Рис.1.8.
в Рис.1.8.


 Исходные данные представлены на схеме.
Исходные данные представлены на схеме.
 = 4,997 om;
= 4,997 om;
 6,039 е -j46 om.
6,039 е -j46 om.



 4. Oпpeделяем нaпpяжения U1 и Uab
4. Oпpeделяем нaпpяжения U1 и Uab



 I 2 = U АВ /Z 2 = 55,433 * e j62 / 3 = 18, 4778 * e j62 = 8,566 + j 16, 372 А
I 2 = U АВ /Z 2 = 55,433 * e j62 / 3 = 18, 4778 * e j62 = 8,566 + j 16, 372 А
 I 1 = 17,06 + j18, 052 = I2 + I з = (8, 566 + j16, 372) + (8, 5 + j1,662) =
I 1 = 17,06 + j18, 052 = I2 + I з = (8, 566 + j16, 372) + (8, 5 + j1,662) =

 Построим векторную диаграмму токов на комплексной плоскости
Построим векторную диаграмму токов на комплексной плоскости
 I 1 – I 2 - Iз = 0.
I 1 – I 2 - Iз = 0.
 Е=150е j0 В,
Е=150е j0 В,
 U 1 = I 1 *Z 1 = 24,838 e j46 * 5,381 e j68 = 133,653 * e -j21. = 124,3 - j 49,116 B.
U 1 = I 1 *Z 1 = 24,838 e j46 * 5,381 e j68 = 133,653 * e -j21. = 124,3 - j 49,116 B.

 UR 3= I 3 *R3= 8,662 e j11 *4=34,8 e j11;
UR 3= I 3 *R3= 8,662 e j11 *4=34,8 e j11;
 uab = UR2;
uab = UR2; 



