
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поверхностный потенциальный барьерСодержание книги
Поиск на нашем сайте
Электроны проводимости свободно перемещаются по всему металлу, однако не могут выходить за его пределы. Их выходу наружу препятствуют силы, действующие у поверхности металла. Эти силы имеют электрическую природу и действуют в узкой области вблизи поверхности металла, которую называют потенциальным барьером. Работа, которую должен совершить электрон, покидая кристалл, равна
Величина Для металлов Тот факт, что при низких температурах электронная эмиссия падает до неизмеримо малой величины, позволяет заключить, что для всех металлов полная работа выхода значительно превышает уровень Ферми (рис.2.11). Как видно из рис.2.11, иллюстрирующего энергетическое состояние электронного газа в твердом теле, энергией, достаточной для эмиссии, обладают только электроны, число которых изображается площадью кривой
Термоэлектронная эмиссия
Эмиссия электронов и ионов – это выход заряженных частиц, происходящий на границе твердого тела с вакуумом или газом при воздействии на эмиттер теплового нагрева, светового излучения, электронной или ионной бомбардировки, постоянного или высокочастотного электрического поля и т.д. Явление испускания в вакуум электронов нагретым телом называется термоэлектронной эмиссией. Установлено, что при Т = 0 не может быть эмиссии электронов из кристалла, поскольку энергии даже самых быстрых электронов недостаточны для преодоления потенциального барьера на его границе. При нагревании твердого тела возрастают амплитуды колебаний атомов кристаллической решетки. С повышением температуры все большее число электронов (рис.2.10) приобретает энергию, достаточную для преодоления потенциального барьера на границе твердого тела с вакуумом. Если в каждом кубическом метре металла содержится dnu За пределы поверхности кристалла в вакуум могут выйти только электроны, у которых компонента скорости в направлении х достаточна для преодоления потенциального барьера, т.е.
Для определения числа электронов, покидающих в единицу времени 1 м2 поверхности металла при данной температуре, надо в формулу подставить функцию распределения электронов по скорости в металле и проинтегрировать полученное выражение. Согласно квантомеханической теории, не все электроны выходят в вакуум, есть вероятность отражения их от потенциального барьера. Поэтому вводится понятие прозрачности барьера D. Уравнение Ричардсона-Дешмана определяет плотность тока термоэмиссии:
где Энергия Ферми определяется соотношением
где Уравнение Ричардсона-Дешмана показывает, что плотность тока термоэлектронной эмиссии с поверхности металла зависит от температуры и эффективной работы выхода материала. Уравнение определения плотности тока термоэмиссии применимо не только к металлическим, но и к полупроводниковым катодам любого типа. Специфика состоит, однако, в том что, если у металлов положение уровня Ферми можно было в первом приближении считать не зависящим от температуры и рассматривать jэфф. как постоянную данного материала, то у примесных полупроводников положение уровня Ферми зависит от температуры. Температурный коэффициент работы выхода (a) был определен для металлов êa½ ~ 10 –5 Распределение по скоростям эмиттированных из металла электронов (при термоэмиссии) описывается функциями распределения Максвелла-Больц-мана, т.е. эмиттированные электроны можно рассматривать как невырожденный идеальный газ.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 1038; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.192.250 (0.006 с.) |


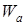 характеризует полную высоту потенциального барьера на границе металла и называется полной работой выхода.
характеризует полную высоту потенциального барьера на границе металла и называется полной работой выхода.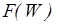 выше уровня
выше уровня 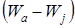 и не очень высокой температуре. Величина
и не очень высокой температуре. Величина 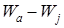 , равная наименьшей энергии, которую должен получить электрон при Т=0° С, чтобы совершить акт эмиссии, называется эффективной работой выхода (
, равная наименьшей энергии, которую должен получить электрон при Т=0° С, чтобы совершить акт эмиссии, называется эффективной работой выхода ( ).
).
 ,u
,u 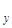 , u
, u 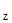 свободных электронов с компонентами скоростей от uх до uх + duх, от uy до uy + +duy и от uz до uz + duz, (где uх – компонента скорости в направлении, перпендикулярном поверхности тела), то поток таких электронов, приходящий к поверхности равен
свободных электронов с компонентами скоростей от uх до uх + duх, от uy до uy + +duy и от uz до uz + duz, (где uх – компонента скорости в направлении, перпендикулярном поверхности тела), то поток таких электронов, приходящий к поверхности равен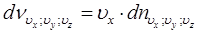
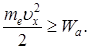
 ,
,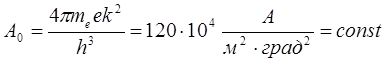 является универсальной постоянной и не зависит от рода эмиттера.
является универсальной постоянной и не зависит от рода эмиттера.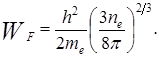 Видно, что
Видно, что 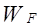 не зависит в первом приближении от температуры и поэтому
не зависит в первом приближении от температуры и поэтому 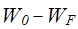 можно заменить эффективной работой выхода
можно заменить эффективной работой выхода 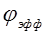 , тогда
, тогда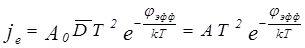
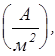
 . и полупроводников a ~ 10 –4
. и полупроводников a ~ 10 –4  влияет большое количество факторов и нет точного определения его, что
влияет большое количество факторов и нет точного определения его, что 


