Дифференциальное включение ОУ.

 

Схема дифференциального включения ОУ приведена на рис.14.6.

 

R ос

R 1

U с1

U с2	R 2	U Вых

R 3

 

Рис.14.6. Дифференциальное включение ОУ

 

Для дифференциального усилителя принципиальным условием работы схемы является идентичность обоих каналов усиления. Чтобы обеспечить равенство коэффициентов усиления обоих каналов схемы необходимо выполнение условия:

^R ос		^R 3	(14.8)
^R 1	^R 2

В этом случае для инвертирующего входа входное сопротивление равно

R ₁,для не инвертирующего входа– R ₂ R ₃.Для устранения этого недостаткасигнал на входы подают через повторители напряжения.

 

 

Сумматоры на ОУ.

 

 

Рис.14.7. Схема инвертирующего сумматора на ОУ

 

При анализе работы схемы будем пренебрегать входными токами ОУ.

 

Тогда:

 

^U вых ^I R ос ^.

(14.10)

Согласно первому закону Кирхгофа I

I 1

I 2.Поскольку потенциалы

в точках a и b равны:

^I 1

^U c1

;

^I 2

^U c2

.

(14.11)

R

R

Следовательно,

n

Ui

^U вых ^R ос

.

(14.12)

R

i 1 ^i

Таким образом, выходное напряжение будет пропорционально сумме входных напряжений. Чтобы веса в этой сумме были одинаковы для всех входных сигналов следует выбирать равными сопротивления R_i. В некоторых схемах специально выбирают веса разными с тем, чтобы определить важность поступающей информации по какому-либо каналу.

 

Для того чтобы получить положительный коэффициент используют

 

неинвертирующий сумматор:

 

Рис.14.8. Принципиальная схема неинвертирующего сумматора на ОУ

 

Следует отметить, что в такой схеме развязка между входами хуже, чем в предыдущей схеме. Для увеличения развязки необходимо увеличивать сопротивление R ₀, чтобы уменьшить токи I_i.

 

Для получения коэффициента суммирования как со знаком «+», так и со знаком «–» обе схемы сумматоров объединяют:

 

Рис.14.9. Принципиальная схема полного сумматора на ОУ

 

 

Дифференциаторы на ОУ

 

 

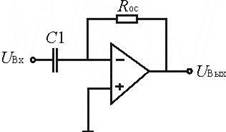
Рис.14.10. Принципиальная схема идеального дифференциатора на ОУ

 

Ток через емкость определяется выражением:
i C	dU вх		(14.13)
c	dt

Если предположить, что ОУ является идеальным, то I_R i_c. Поскольку:

 

	U вых IRR ос,	(14.14)
то выходное напряжение оказывается пропорционально первой
производной от входного сигнала:
U	вых	i R RC	dU вх	(14.15)
	c	dt

 

Приведенная на рис.14.10 схема будет работать не во всем частотном диапазоне: при увеличении частоты сопротивление емкости C стремиться к нулю, а, следовательно, коэффициент усиления бесконечно возрастает. Для того чтобы схема работала устойчиво необходимо снизить коэффициент усиления за пределами рабочей полосы частот.

 

 

Рис.14.11. Принципиальная схема реального дифференциатора на ОУ

 

 

Емкость C _доп выбирается таким образом, чтобы участок характеристики со спадом 6 дБ/октава начинался на частоте более высокой, чем верхняя граничная частота дифференцируемого сигнала:

f 2		.	(14.16)
	2 RC доп

Сопротивление R _доп ограничивает коэффициент усиления на высоких частотах, обеспечивает динамическую устойчивость и снижает входной емкостной ток схемы, «отбираемый» от источника сигнала. Наличие в схеме сопротивления R _доп приводит к прекращению дифференцирования на частотах, больших f ₁:

 

f 1		.	(14.17)
	2 CR доп

Выходное напряжение схемы рис.14.11 имеет:

 

^U вых	RC	dU вх	.	(14.18)
		dt

Интеграторы на ОУ

 

K

 

 

f

 

Рабочий диапазон

Рис.14.12. Принципиальная схема идеального интегратора на ОУ и его АЧХ

 

Выходное напряжение схемы оказывается пропорциональным входному интегралу входного напряжения:

		t
U Вых	U Вх t dt Uc 0,	(14.19)
RC

 

где U_c 0 – начальное напряжение на емкости, то есть постоянная

 

интегрирования.