Методы направленного поиска экстремумов.

Это пошаговые методы, на каждом шаге используется информация предыдущих шагов.

5.1 Методы определения экстремума унимодальной функции.

Унимодальная функция – функция, в интервале исследования имеющая только один экстремум.

А) Методы определения экстремума функции одной переменной.

Идея методов:

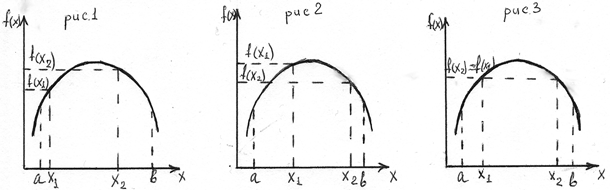
На каждом шаге выбирается 2 точки X₁ и X₂ в них определяются значения целевой функции, они сравниваются.

На рис. 1 f (X₁)< f (X₂), тогда из дальнейшего рассмотрения удаляется интервал [a, X₁], т.к. там не будет экстремума.

На рис. 2 f (X₁)> f (X₂), тогда в интервале [X_2, b] не может быть экстремума, если функция унимодальная.

На рис. 3 f (X₁)= f (X₂), тогда исключаются [a, X₁] и [X_2, b].

Б)Метод половинного деления (дихотомии).

Дана целевая функция, она унимодальна.

1. Если область изменения переменной неограниченна, то ее надо ограничить.

2. Интервал исследования делится пополам. Выбирается точность получения результата (интервал, внутри которого будет находится экстремум).

3. Заданный интервал делится пополам ∆Х/2, полученные величины откладываются от т. С влево и вправо. Получаем две точки X₁ и X₂.

4. В т. X₁ и X₂ вычисляется значение целевой функции.

5. Затем, используя свойство унимодальности целевой функции удалить из рассмотрения один из полученных интервалов и перейти на шаг 2.

В) Метод Фибоначчи.

В основе метода лежат числа Фибоначчи.

N
FN

 

 

N – порядковый номер;

F₀= F₁=1; F_N= F_N+1+ F_N-2

Задана целевая функция f (X) и точность ∆Х.

Алгоритм метода.

1. Находится некоторое число F= l/ ∆Х, допустим F′ = 10(9)

2. Выбирается ближайшее наибольшее число Фибоначчи (F_N = 13, N = 6)

3. Находится новая точность получения результата ∆Х′ = l/ F_N.

4. Зафиксировать 2 точки X₁ и X₂ следующим образом:

X₁ = а + F_N-2 * ∆Х’

X₂ = b - F_N-2 * ∆Х’

5.Вычисляется значения f (X₁) и f (X₂).

6. Используя свойство унимодальности – удалить из дальнейшего рассмотрения один из интервалов, в данном случае [X_2, b].

Переход к новому циклу:

Анализируется интервал [a, X₂]. От его концов откладываются новые точки X₃ и X_4. Их величина F_N-3 * ∆Х’ (∆Х′ – то же порядковое число Фибоначчи ↓ на 1)

Причем из двух точек, полученных на каждой следующей итерации – одна известна, то есть нужно вычислить значение целевой функции только в одной оставшейся неизвестной точке.

Преимущество метода:

Нет необходимости вычислять два новых значения Х, а только одно значение аргумента и целевой функции. Метод Фибоначчи работает быстрее метода дихотомии.

Недостаток метода:

Подготовительная работа по заготовке таблиц Фибоначчи.

Г) Метод золотого сечения.

Задана целевая функция f (X), ограничения [a,b], точность получения результата ∆Х.

Если выполняется условие аb/ас=ас/ cb, то это золотое сечение.

1) от концов интервала l откладываем интервалы aX₂= bX₁ = (1/1,62)∙ l получаем точки X₁ и X₂.

2) определяются значения f (X₁) и f (X₂).

3)используя свойство унимодальности, удалить из рассмотрения один из крайних отрезков (в случае поиска max - [X_2, b]). Остался интервал [a, X₂] длиной l₁. От его концов откладываются отрезки длиной (1/1,62)∙ l₁. При этом одна из точек совпадает с одной из точек, оставшейся от предыдущей итерации.

 

5.2 Методы определения локального экстремума функции нескольких переменных

а) Метод Гаусса – Зейделя

Метод поочередного изменения параметров (переменных), или метод покоординатного спуска (подъема).

Суть метода: поочередная оптимизация последовательно по каждой переменной.

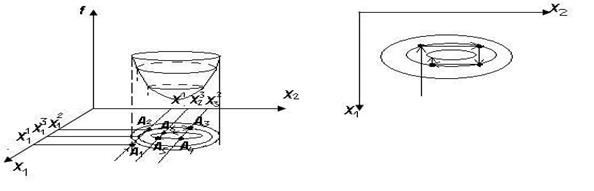
Обрабатывается функция n переменных. По каждой переменной задана область изменения. Случайным образом выбирается т. А₁.

А₁:х₁^′,х₂^′, х₃′,…, х_n′ => f( х₁^′,х₂^′ , х₃′,…, х_n′ )

⁼

х₁ рассматривается в целевой функции, а другие переменные фиксируются. Применяется один из рассмотренных ранее методов. Затем находится т.А_2.

А₁:х₁²,х₂^′, х₃′,…, х_n′ => f( х₁², х₂^′ , х₃′,…, х_n′ )

⁼

Берется следующая переменная – х₂. Целевую функцию рассматриваем как функцию переменной х₂,остальные переменные фиксируются. Используем один из методов для функции одной переменной и получаем т. А₃.

А₃=:х₁²,х₂², х₃′,…, х_n′ и т.д. процесс повторяется.

Характерные черты метода: Спираль выбранных точек имеет прямые углы. Метод обеспечивает поиск только локального экстремума. Результаты анализа целевой функции зависят от первоначально выбранной точки.

Преимущество: простота алгоритмизации. Алгоритм останавливается, когда разница между значениями целевой функции достаточно мала (она задается).

б) Метод градиента(наиболее распространен)

Суть метода: нахождение направления движения, в котором целевая функция наибольшим образом изменяется и осуществление следующего шага в этом направлении.

Градиент функции – вектор, который характеризует направление наибольшего возрастания функции.

Антиградиент – уменьшение функции. grad f^N (х¹,х²,...,хⁿ)=(∂ f^N/ ∂ х¹_, ∂ f^N/ ∂ х²_,..., ∂ f^N/ ∂ хⁿ), вычисленный в точке N

 

 

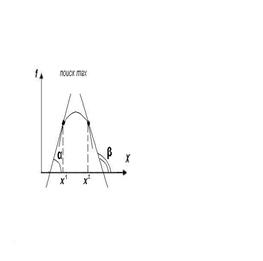
∂ f^N/ ∂ х¹ = tgα > 0(≤α < 90 ^*) - значит ∂ f^N/ ∂ х¹ = tgα <0 - значит нужно шагать вправо(увеличивать х). нужно шагать вправо(увеличивать х).

∂ f^N/ ∂ х² = tgβ< 0(≤α > 90 ^*) - ∂ f^N/ ∂ х² = tgβ> 0 - значит нужно шагать влево.

значит нужно шагать влево (уменьшать х).

(уменьшить х).

 

Для max следующая точка х^N+1 = x^N+ (∂ f^N/ ∂ хⁿ) ∙ h

h- вспомогательная величина.

Если ∂ f^N/ ∂ хⁿ =0, то в этой точке экстремум.

Для min следующая точка х^N+1 = x^N- (∂ f^N/ ∂ хⁿ) ∙ h

В случае n- мерного пространства:

_

х_i ^N+1=x_i^N+(∂ f^N/ ∂х_iⁿ)∙h; i=1,n – max

_ (1)

х_i ^N+1 = x_i^N - (∂ f^N/ ∂ х_i ⁿ) ∙ h; i=1, n - min

 

 

Алгоритм метода

Случайно выбираемся точка с некоторыми координатами. Затем по формуле (1) рассчитывается следующая точка.

Алгоритм останавливается либо при уменьшении модуля рабочего шага, либо по значению целевой функции.

Модуль рабочего шага

b=h

 

Преимущества:

-метод сходится быстрее.

Недостаток:

-необходимость вычислять частные производные.

в) Метод наискорейшего спуска

Представляет собой ускоренный метод градиента

При поиске min

f(x₁, x₂, … x_m)- целевая функция

x_i^N+1=x_i^N – t ∂f/∂x_i^N = x(t) i=1, … m

будем считать t – переменной

f(x₁(t), x₂(t),...,x_m(t)) = (t), в этом случае целевая функция есть функция одной переменной t.

Составим уравнение =0, найдем t*.

 

x_i^N+1=x_i^N – t^* ∂f/∂x_i^N

чем ближе к min – тем меньше , тем меньше шаг надо делать.