
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отыскание опорного и оптимального решения злп с использованием табличного алгоритма с заменой базисных переменных.Содержание книги
Поиск на нашем сайте
Алгоритм составления симплексных таблиц (СТ), рассмотрим на примере решения задачи отыскания max. Пример 2.6 Линейная функция: F=2x1+3x2→max Система ограничений
2x1+x2≤16 x2≤5 3x1≤21 x1, x2≥0
1. Приведем эту систему к каноническому виду, введя дополнительные переменные х3, х4, х5, х6:
2х1+х2+х 4=16 х2+х5=5 3х1+х6=21
Целевую функцию представим в виде: F-2x1-3x2=0;
2. Заполняем первую симплексную таблицу: в ней х3, х4, х5, х6 – основные переменные (базис). Последняя строка называется оценочной. Таблица №1.
←разрешающая строка
↑ разрешающий столбец
3. Проверяем выполнение критерия функции на max – первый опорный план не оптимальный, так как в F коэффициенты при x1 и x2 < 0
4. Выбираем наибольший по модулю отрицательный коэффициент F, который определяет разрешающий столбец.(второй столбец)
5. Делим свободные члены на коэффициенты разрешающего столбца, определяем оценочные отношения. И выбираем строку в качестве разрешающей, где это отношение минимальное min {6,16,5,∞}=5. На пересечении разрешающего столбца и разрешающей строки находиться разрешающий элемент a23 = 1. Для построения таблицы №2 в качестве основной переменной мы выбираем х2, так как она образует разрешающей столбец таблице 1. Переход к новому плану осуществляется пересчетом симплексной таблице (СТ) методом Жордана Гаусса.
Таблица №2.
← разрешающая строка
↑ разрешающий столбец
Построение 2ой таблицы: 1)Заменим переменные в базисе с х5 на х2. 2)Делим элементы разрешающей строки х5 (табл.1) на разрешающий элемент, результаты занесем в строку х2, но в таблицу №2. 3)В остальных клетках разрешающегося столбца (табл.1) записываем 0. 4)Остальные клетки заполняем по правилу прямоугольника:
НЭ- новый элемент. СТЭ- старый элемент. РЭ- разрешающий элемент. А,В- эл-ты старого плана, образующие прямоугольник со старым эл-том и разрешающим элементом.
СТЭ А
В РЭ
b1=18-(3х5)/1=3 а11=1-(3х0)/1=1 b2=16-(1х5)/1=11 и т.д. Критерии оптимальности опять не выполнен, так как F имеет коэффициент -2<0 - наибольший отрицательный по модулю коэффициент |-2| определяет разрешающий столбец x1
- min (3;11/2;∞;7)=3. Следовательно, 1ая строка разрешающая а11 - разрешающий элемент.
Таблица №3
← разрешающая строка
↑ разрешающий столбец В таблице 3 критерий оптимальности вновь не выполнен. Разрешающий столбец x5, разрешающая строка x4, разрешающий элемент 5. 1)х1 вместо х3. 2)В строке х1 делим все на 1.
Таблица №4
Новая СТ№4 – критерий оптимальности выполнен – оптимальное базисное решение X(6,4,0,0,1,3) F=24 =max Вспоминая экономический смысл всех переменных, логично сделать следующие выводы. Прибыль принимает максимальное значение Fmax=24 при реализации 6 единиц продукции P1 (x1=6) и 4 единиц продукции P2(x4=4). Дополнительные переменные x3, x4, x5, x6 показывают остатки ресурсов каждого вида. При оптимальном плане производства x3=x4=0, то есть остатки ресурсов S3 и S4 равны 0, а остатки ресурсов S5 и S6 равны соответственно 1 и 3 единицам. Выполнить самостоятельно. В соответствии с индивидуальным заданием №1 решить задачу максимизации с использованием симплексных таблиц. Вариант задания выбирается по номеру зачетной книжки: -предпоследняя цифра - № столбца -последняя цифра – № строки Пример: Симплексным методом решить задачу максимизации. F(x)=5x1-x2→max 2x1-x2+x3≤3 3x1+2x2≤6 x1≥0; x2≥0 1. Переведем систему ограничений в канонический вид, введя выравнивающие (базисные) неизвестные – x3 и x4. Задача принимает следующий вид: 2x1-x2+x3=3 3x1+2x2=6 x1=x2=x3=x4=0 F-5x1+x2=0 2. Заполняем первую симплексную таблицу. В ней x3, x4 – основные переменные (базис). Таблица 1.
← разрешающая строка
↑ разрешающий столбец
3. Проверяем выполнение критерия на max – первый опорный план не оптимальный, т.к. в F коэффициент при х1<0 4. Выбираем наибольший по модулю отрицательный коэффициент F, который определяет разрешающий столбец.
5. Делим свободные члены на коэффициенты разрешающего столбца (определяем оценочные отношения). Выбираем разрешающую строку, где это отношение минимально
Min (3, 2)= 3 2 2 Разрешающий элемент будет а11=2 Для построения таблицы 2 в качестве основной переменной выбираем х1, т.к. она образует разрешающий столбец таблицы 1.
Таблицы 2.
← разрешающая строка
↑ разрешающий столбец Построение таблицы №2. 1. Заменим переменные в базисе с х3 на х1. 2. Делим элементы разрешающей строки (табл.1) на разрешающий элемент, результаты занесем в строку х1 в табл. №2. 3. В остальных клетках разрешающего столбца (табл. 1) записываем 0. 4. Остальные клетки заполняем по правилу прямоугольника НЭ=СТЭ-(АхВ)/РЭ
СТЭ А
В РЭ
5. Критерий эффективности опять не выполнен, т.к. F имеет два коэффициента - 3 < 0 Построение таблицы №3 Таблицы 3.
Из таблицы 3 видно – критерий оптимальности выполнен. Оптимальные базисные решения Х*=(12, 3,0,0) 7 7 F=5x1-x2=5x 12 - 3 = 57 7 7 7
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ №1
Пример. Решить следующую задачу максимизации F(x)=5x1-x2→max 2x1-x2+x3≤3 3x1+2x2≤6 x1≥0; x2≥0
Запишем систему в каноническом виде 1) 2x1-x2+x3=3 2) 3x1+2x2=6 3) x1=0; x2=0
Решение. В системе координат Х1ОХ2 построим ОДР.
При Х1=0 X2=-3 → (X1,X2)=(0,-3) прямая (1) При Х2=0 Х1= 3 → (X1,X2)=(3, 0) 2 2
При Х1=0 X2=3 → (X1,X2)=(0,3) прямая (2) При Х2=0 Х1=2 → (X1,X2)=(2, 0)
Из условия (3) (Х1, Х2)=(0,0) Х1=0 – прямая (3) Х2=0 – прямая (4)
Для определения с какой стороны прямых ОДР все точки удовлетворяют неравенствам возьмем точку (1,1). Таким образом, ОДР лежит внутри АВСD. Для определения точки выхода, строим прямую: F(x)=5x1-x2=0 5x1=x2→ x1=x2=0 при x1=1, x2=5 Строим нулевую линию уровня целевой функции. Строим нормальный вектор q (5.-1) Передвигая линию уровня целевой функции параллельно себе, по вектору q, фиксируем ее крайнее положение (т.В), которая принадлежит прямым (1) и (2).
2x1-x2+x3=3 3x1+2x2=6
x1= 12 x2= 3, т.е. Х*=(12, 3) 7 7 7 7 F(Х*)=5х 12 - 3 = 57 7 7 7
2.8Двойственные задачи линейного программирования (ДЗЛП). Рассмотрим пример 2.6 и пример 2.5 и представим их в виде таблице
Из таблице видно, что задачи 1 и 2 обладают следующими свойствами: 1) В задаче 1 ищут max, во 2 ищут min. 2) Коэффициенты целевой ф-ции 1-ой задачи являются свободными членами системы ограничения 2-ой задачи. 3) Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида ≤, а в задаче минимизации вида ≥. 4) Матрицы коэффициентов в системе ограничения обеих задач являются транспонированными друг другу.
задачи 1 A1= 2 1 16 0 1 5 3 0 21 2 3 F
Для задачи 2 A’1= 1 2 0 3 2 3 1 1 0 21 18 16 5 21 Z
5) Число неравенств в системе ограничений 1-ой задачи совпадает с числом переменных 2-ой задачи. 6) условие не отрицательности переменных есть в обеих задачах. Две задачи, обладающие указанными свойствами, называются симметричными взаимно – двойственными задачами. 2.9Алгоритм составления двойственных ЗЛП: Исходя из вышесказанного логично предложить следующий алгоритм: 1) Привести все неравенства системы ограничений исходной задачи к одному смыслу: если в исходной задаче ищут max целевой функции, то все неравенства системы ограничений привести к виду ≤, а если ищут min – к виду ≥. Для этого неравенства, в которых это требование не выполняется, умножить на (-1). 2) Составить расширенную матрицу системы A1. 3) Найти матрицу A1, транспонированную к матрице A1. 4) Сформулировать двойственную ЗЛП Этот алгоритм можно проиллюстрировать следующим примером: Составить задачу двойственную следующей задаче: F=14x1+10x2+14x3+11x4→max Система ограничений:
х1+х2+2х3+3х4≤30 3х1+х2+2х3+х4≥40* х1≥0 х2≥0 х3≥0 х4≥0
Решение:
Выполнить самостоятельно: 1. Составить ДЗЛП следующей задачи
При ограничении: 2x1-x2≥1 -x1+4x2≤24 x1 -x2≤3 x1 +x2≥5 2. Составить ДЗЛП, используя исходные данные таблицы №1. Вариант задания выбирается по номеру зачетной книжки –предпоследняя цифра - № строки –последняя цифра - № столбца. 3.Теорема двойственности
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 158; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.116.234 (0.008 с.) |

 x1+3x2≤18
x1+3x2≤18 х1+3х2+х3=18
х1+3х2+х3=18




 Из первого уравнения:
Из первого уравнения:
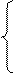 x1+3x2≤18
2x1+x2≤16
x2≤5
3x1≤21
x1, x2≥0
Составить такой план выпуска продукции X=(x1, х2) при котором прибыль при реализации будет max.
В общем виде задача запишется:
n
F=∑Cjxj→max,
j=1
при ограничениях:
n j=1,2…m
∑aijхi≤ bi i=1,2…n
j=1
x1+3x2≤18
2x1+x2≤16
x2≤5
3x1≤21
x1, x2≥0
Составить такой план выпуска продукции X=(x1, х2) при котором прибыль при реализации будет max.
В общем виде задача запишется:
n
F=∑Cjxj→max,
j=1
при ограничениях:
n j=1,2…m
∑aijхi≤ bi i=1,2…n
j=1
 y1+2y2+3y4≥2
3y1+y2+y3≥3
y1, y2, y3, y4≥0
Найти такой набор цен ресурсов Y=(y1,y2,y3,y4), при котором общие затраты на ресурсы будут минимальны.
В общем виде задачу запишем:
m
Z=∑ biyi →min,
i=1
при ограничениях:
m j=1,2…m
∑ aijyi≤ cj i=1,2…n
i=1
y1+2y2+3y4≥2
3y1+y2+y3≥3
y1, y2, y3, y4≥0
Найти такой набор цен ресурсов Y=(y1,y2,y3,y4), при котором общие затраты на ресурсы будут минимальны.
В общем виде задачу запишем:
m
Z=∑ biyi →min,
i=1
при ограничениях:
m j=1,2…m
∑ aijyi≤ cj i=1,2…n
i=1

 Для 1 3 18
Для 1 3 18 4х1+2х2+2х3+3х4≤35
4х1+2х2+2х3+3х4≤35

 4 1 -3 14
4 1 -3 14
 F=-x1+2x2→max
F=-x1+2x2→max


