
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Место и роль методов оптимизации при моделировании и решении прикладных задач.Стр 1 из 7Следующая ⇒
МЕТОДЫ ОПТИМИЗАЦИИ Курс лекций Перевод в электронный вид осуществляли студенты факультета ИСТАС Горин А.С. Овсянникова М.В. Москва 2009 г. МЕТОДЫ ОПТИМИЗАЦИИ 1. Основные понятия и определения. Место и роль методов оптимизации при моделировании и решении прикладных задач. Исследование операций – научная дисциплина, занимающаяся разработкой и практическим применением методов эффективного управления различными организационными системами. Цель исследования операций – количественное обоснование принимаемых решений по организации управлений. При решении задач управления применение методов исследования предполагает: - изучение взаимосвязей и установление критериев эффективности, позволяющих оценивать преимущество того или иного варианта; - постановку задачи принятия решения в сложных ситуациях или в условиях неопределенности. К задачам исследования можно отнести задачи об использовании ресурсов (планирование производства), о смесях, об использовании мощностей (загрузке оборудования), о раскрое материалов, транспортную задачу и другие, в которых требуется найти решение, когда некоторый критерий эффективности (например, прибыль, выручка, затраты ресурсов и т.п.) принимает максимальное и минимальное значение. В каждом случае речь идет о каком-то управляемом мероприятии (операции), преследующем определенную цель. В каждой задаче заданы некоторые условия, в рамках которых необходимо принять решение. Основными понятиями являются: Операция – любое управляемое мероприятие, направленное на достижение целей. Результат операции зависит от способов ее проведения (от выбора некоторых параметров). Решение – определенный выбор параметров. Оптимальное решение – те решения, которые предпочтительнее других. Модель операции – описание операции с помощью математического аппарата. Эффективность операции количественно выражается в виде критерия эффективности - целевой функции. Например: - в задаче об использовании ресурсов критерием эффективности является прибыль от реализации произведенной продукции, которую надо максимизировать; - в задаче транспортного типа критерием эффективности является суммарные затраты на перевозку грузов, которые надо минимизировать.
Общая постановка прикладной задачи. Все факторы, входящие в описание модели можно разделить на две группы: внешние факторы (условия проведения операции), на которые мы не можем влиять а1,а2,а3,…; Зависимые факторы (элементы решений), которые мы можем выбирать х1,х2,х3,… Величина критерия эффективности выражается некоторой функцией, называемой целевой функцией. Она зависит от факторов обеих групп и записывается в виде: z = f (x1 x2 … a1 a2 …) Оптимизационная задача формулируется в общем виде. Найти переменные х1,х2,…хn, удовлетворяющие системе неравенств (уравнений) φj (x1 x2…xn) ≤ bj, где j =1, 2, …m, и обращают в max или min целевую функцию: z = f (x1, x2,…a1, a2,…) → max (min).
Основные этапы построения оптимизационных моделей. Основные этапы построения оптимизационных моделей можно представить в виде схемы:
Последовательность моделирования представляет собой итерационную процедуру, которая предусматривает проведение коррекции после каждого этапа и возможность вернуться к любому из предшествующих, а затем продолжить анализ.
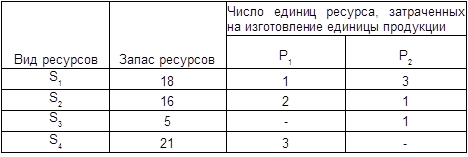
Линейное программирование. Пример постановки задачи линейного программирования. В качестве примера рассмотрим задачу об использовании ресурсов. Пример. Для изготовления 2-х видов продукции Р1 и Р2 используют 4 вида ресурсов S1, S2, S3,S4. Запасы ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице:
X1, X2– число единиц продукции. Прибыль, получаемая от единицы продукции Р1 и Р2 соответственно равны С1=2 и С2=3. Так как потребление ресурсов S1, S2, S3,S4 не должно превышать их запасов, то связь между потреблением ресурсов и их запасами выразится системой неравенств:
х1 + 3х2 ≤ 18 2х1 + х2 ≤ 16 (2.1) – система ограничений. х2 ≤ 5 3х1 ≤ 21
По смыслу задачи переменные x1≥0, x2≥0 (2.2) Суммарная прибыль составит F = 2x1 + 3x2→max (2.3) Итак, экономико-математическая модель задачи найти план выпуска продукции, Х (х1,х2) удовлетворяющий системе ограничений (2.1) и условию (2.2), при которых функция (2.3) принимает максимальное значение. Задачу легко обобщить на случай n видов продукции с использованием m видов ресурса.
Примеры прикладных ЗЛП. Пример 2.1 Для производства двух видов изделий А и В предприятие использует 3 вида сырья. Запасы ресурсов, число единиц ресурсов, затрачиваемые на изготовление единицы продукции, а также прибыль, получаемая от единицы продукции, приведены в таблице:
Решение. X1, X2– число единиц видов изделий соответственно А и В.
Выполнить самостоятельно: Пример2.2 Рацион для питания животных на ферме состоит из двух видов кормов: I и II. 1 кг I корма стоит 80 руб. и содержит 1 ед.жиров, 3 ед.белков и 1 ед.углеводов. 1 кг II корма стоит 10 руб. и содержит 3 ед.жиров, 1 ед.белков и 8 ед.углеводов. Составить наиболее дешевый рацион питания, обеспечивающий жирами не менее 6 ед., белками не менее 9 ед., углеводами не менее 8 ед. Пример 2.3 Решить графическим методом следующую задачу:
3х1 + 2х2 ≤ 21 3х1 + х2 ≤ 18 х1; х2 ≥ 0
Определить при каких х1 и х2 функция F = 30х1 +60х2 → max
4) х1 = 0 5) х2 = 0 Прямые пронумерованы, а рядом с соответствующим уравнением приведены координаты двух точек, через которые проходят прямые. В результате получим выпуклый пятиугольник ОАВСD.
2. Строим нормальный вектор q = (30;60)/ 3, уменьшив значение координат в 3 раза. Прямая с уравнением 30 х1 + 60 х2 = 0 представляет собой «нулевую» линию уровня целевой функции. Эта прямая проходит через начало координат и перпендикулярна нормальному вектору q. Передвигаем эту прямую параллельно себе по вектору q и фиксируем ее крайнее положение (т.В).
3. Определим координаты точки В, которая принадлежит прямым 1) и 2). Составляется система уравнений:
3х1 + 2х2 = 21
Тогда F max =30∙3 + 60∙6 = 450 При минимизации F = 30 х1 + 60 х2 линию уровня необходимо смещать параллельно самой себе в направлении противоположном вектору q. Минимум функции достигается в точке О(0;0). Тогда F min = 0.
К достоинствам геометрического метода решения ЗЛП относятся: - наглядность; - быстрота и легкость нахождения ответа.
К недостаткам геометрического метода относятся: - возможны «технические» погрешности при приближенном построении графиков; - многие величины, имеющие четкий экономический смысл (остатки ресурсов производства, избыток питательных веществ и т.п.) не выявляются; - этот метод легко применим, когда число переменных в стандартной задаче не превышает двух.
Выполнить самостоятельно. ЗАДАНИЕ №1. В соответствии с заданием (табл. 1) решить задачу оптимизации графически. В задаче построить многоугольник допустимых решений. На многоугольнике определить точку выхода, определить координаты этой точки и значение целевой функции в точке выхода.
ТАБЛИЦА №1
2.5 Элементы линейной алгебры. Любые m переменных системы уравнений с n переменными, где m < n называются основными (или базисными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные n – m переменных называются неосновными (или свободными). Основными могут быть разные группы из n переменных. Максимальное число групп основных переменных равно числу сочетаний Пример 2.4. Решить систему уравнений
2 х1 + х2 + 2х3 – х4 = 2
Общее число групп основных переменных: Выясним, могут ли быть основными переменные X1X2 , т.к. определитель матрицы из коэффициентов ׀ 1 -1 ׀ = 1•1 – 2•(-1) ≠ 0, ׀ 2 1 ׀ то X1X2 – основные переменные Аналогично основным можно отнести X1X3; X1X4 (у них определители ≠ 0) Группы X2X3, X2X4, X3X4 не могут быть основными, т.к. их определители = 0
Таким образом система уравнений имеет 3 базисных решения: 1) Для основных переменных X1X2 и не основных X3X4 (X3= X4 = 0)
Х1-Х2=0 X1 = ⅔ 2Х1+Х2=2 X2 = ⅔
Таким образом, базисное решение: X = (⅔, ⅔, 0, 0) – допустимое решение; 2) Для основных переменных X1X3 и неосновных X2 = X4 = 0 X1 = ⅔ X3 = ⅓ Базисное решение: X2 = (⅔, 0, ⅓, 0). Оно тоже допустимое. 3) Для основных переменных X1 X4 и неосновных X2 = X3 = 0 Базисное решение X3 (⅔, 0, 0, -⅔) – недопустимое.
Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины к соседней, в которых целевая функция принимает лучшие значении до оптимального значения. В настоящее время СМ используется для компьютерных расчетов, однако не сложные методы можно решать и вручную. Для реализации СМ необходимо знать 3 основных элемента: 1. способ определения первоначального допустимого базисного решения; 2. правило перехода к лучшему решению; 3. проверка признака оптимальности решении, который состоит в следующем:
- если отсутствуют отрицательные коэффициенты, то решение минимально.
Для нахождения первоначального базисного решения разобьем переменные на две группы – основные и не основные. При выборе основных переменных на первом шаге не обязательно составлять определитель из их коэффициентов и проверять, равен ли он 0. Достаточно ввести дополнительные неотрицательные переменные с учетом правила определения знака дополнительных переменных: Знак «+», если неравенство вида ≤; Знак «-», если неравенство вида ≥.
Алгоритм вычислительной реализации этих трех элементов рассмотрим на следующем примере. Пример 2.5. Решить задачу симплексным методом: z=18 y1+16y2+5y3+21y4 →min при ограничениях:
3y1+y2+y3≥3 y1, y2, y3, y4≥0 Шаг 1: Введем дополнительные переменные y5, y6 со знаком «-», т. к. «≥» получим систему уравнений в канонической форме:
y1+2y2+3y4-y5=2
Если на первом шаге в качестве основных переменных взять дополнительные переменные y5, y6, тогда: y1=y2=y3=y4=0, => y5=-2; y6=-3. У1=(0,0,0,0,-2,-3) – недопустимое базисное решение.
Шаг 2: В данном случае в качестве основных удобно взять переменные y3, y4 в соответствии с правилом выбора основных переменных, сформулированным выше.
1 0
y3, y4 - основные переменные. y1=y2=y6=y5=0 неосновные переменные; Выразим основные переменные через неосновные:
y4=2/3-y1/3-2/3y2+y5/3 y3=3, y4=2/3;
Базисное решение У2=(0,0,3,2/3,0,0) – допустимое решение. Выражаем линейную функцию через неосновные переменные: z=18y1+16y2+5(3-3y1+y6-y2)+21(2/3-y1/3-2/3y2+y5/3)= 29-4y1-3y2+7y5+5y6 Критерии оптимальности не выполняются, т.к. имеются отрицательные коэффициенты при y1 и y2, поэтому Z1 =29 – не является минимальным. Так как функцию Z можно уменьшить за счет перевода в основные любой из переменных у1 и у2, имеющих в выражении для Z отрицательные коэффициенты. Так как у имеет больший по абсолютному значению коэффициент, то начнем с этой переменной.
Шаг 3: y1, y4 - основные переменные. y2, y3, y5, y6=0 – неосновные переменные; После преобразований:
3 3 3 y4= 1 - 5 у2+ 1 у3+ 1 у5- 1 у6; 3 9 9 3 9 z=25- 5 y2+ 1 у3+ 1 у5- 1 у6; 3 9 3 9 y3=(1;0;0;1/3;0;0) – допустимое базисное решение. Z(y3)=25 – не является min, так как имеется отрицательный коэффициент при y2, поэтому переменную y2 переводим в основную.
Шаг 4: y1,y3 – основные переменные. y3, y4, y5, y6=0 – неосновные переменные.
5 3 3 5 5 y2= 3 + 1 у3- 9 у4+ 3 у5- 1 у6 5 5 5 5 5 y3= (4/5;3/5;0;0;0;0) – допустимое базисное решение z=24+y3+3y4+6y5+4y6→min Решение оптимальное, так как в выражении нет отрицательных коэффициентов при неосновных переменных. Z(y4)=24=min
Пример 2.6 Линейная функция: F=2x1+3x2→max Система ограничений
2x1+x2≤16 x2≤5 3x1≤21 x1, x2≥0
1. Приведем эту систему к каноническому виду, введя дополнительные переменные х3, х4, х5, х6:
2х1+х2+х 4=16 х2+х5=5 3х1+х6=21
Целевую функцию представим в виде: F-2x1-3x2=0;
2. Заполняем первую симплексную таблицу: в ней х3, х4, х5, х6 – основные переменные (базис). Последняя строка называется оценочной. Таблица №1.
←разрешающая строка
↑ разрешающий столбец
3. Проверяем выполнение критерия функции на max – первый опорный план не оптимальный, так как в F коэффициенты при x1 и x2 < 0
4. Выбираем наибольший по модулю отрицательный коэффициент F, который определяет разрешающий столбец.(второй столбец)
5. Делим свободные члены на коэффициенты разрешающего столбца, определяем оценочные отношения. И выбираем строку в качестве разрешающей, где это отношение минимальное min {6,16,5,∞}=5. На пересечении разрешающего столбца и разрешающей строки находиться разрешающий элемент a23 = 1. Для построения таблицы №2 в качестве основной переменной мы выбираем х2, так как она образует разрешающей столбец таблице 1. Переход к новому плану осуществляется пересчетом симплексной таблице (СТ) методом Жордана Гаусса.
Таблица №2.
← разрешающая строка
↑ разрешающий столбец
Построение 2ой таблицы: 1)Заменим переменные в базисе с х5 на х2. 2)Делим элементы разрешающей строки х5 (табл.1) на разрешающий элемент, результаты занесем в строку х2, но в таблицу №2. 3)В остальных клетках разрешающегося столбца (табл.1) записываем 0. 4)Остальные клетки заполняем по правилу прямоугольника:
НЭ- новый элемент. СТЭ- старый элемент. РЭ- разрешающий элемент. А,В- эл-ты старого плана, образующие прямоугольник со старым эл-том и разрешающим элементом.
СТЭ А
В РЭ
b1=18-(3х5)/1=3 а11=1-(3х0)/1=1 b2=16-(1х5)/1=11 и т.д. Критерии оптимальности опять не выполнен, так как F имеет коэффициент -2<0 - наибольший отрицательный по модулю коэффициент |-2| определяет разрешающий столбец x1 - min (3;11/2;∞;7)=3. Следовательно, 1ая строка разрешающая а11 - разрешающий элемент.
Таблица №3
← разрешающая строка
↑ разрешающий столбец В таблице 3 критерий оптимальности вновь не выполнен. Разрешающий столбец x5, разрешающая строка x4, разрешающий элемент 5. 1)х1 вместо х3. 2)В строке х1 делим все на 1.
Таблица №4
Новая СТ№4 – критерий оптимальности выполнен – оптимальное базисное решение X(6,4,0,0,1,3) F=24 =max Вспоминая экономический смысл всех переменных, логично сделать следующие выводы. Прибыль принимает максимальное значение Fmax=24 при реализации 6 единиц продукции P1 (x1=6) и 4 единиц продукции P2(x4=4). Дополнительные переменные x3, x4, x5, x6 показывают остатки ресурсов каждого вида. При оптимальном плане производства x3=x4=0, то есть остатки ресурсов S3 и S4 равны 0, а остатки ресурсов S5 и S6 равны соответственно 1 и 3 единицам. Выполнить самостоятельно. В соответствии с индивидуальным заданием №1 решить задачу максимизации с использованием симплексных таблиц. Вариант задания выбирается по номеру зачетной книжки: -предпоследняя цифра - № столбца -последняя цифра – № строки Пример: Симплексным методом решить задачу максимизации. F(x)=5x1-x2→max 2x1-x2+x3≤3 3x1+2x2≤6 x1≥0; x2≥0 1. Переведем систему ограничений в канонический вид, введя выравнивающие (базисные) неизвестные – x3 и x4. Задача принимает следующий вид: 2x1-x2+x3=3 3x1+2x2=6 x1=x2=x3=x4=0 F-5x1+x2=0 2. Заполняем первую симплексную таблицу. В ней x3, x4 – основные переменные (базис). Таблица 1.
← разрешающая строка
↑ разрешающий столбец
3. Проверяем выполнение критерия на max – первый опорный план не оптимальный, т.к. в F коэффициент при х1<0 4. Выбираем наибольший по модулю отрицательный коэффициент F, который определяет разрешающий столбец. 5. Делим свободные члены на коэффициенты разрешающего столбца (определяем оценочные отношения). Выбираем разрешающую строку, где это отношение минимально
Min (3, 2)= 3 2 2 Разрешающий элемент будет а11=2 Для построения таблицы 2 в качестве основной переменной выбираем х1, т.к. она образует разрешающий столбец таблицы 1.
Таблицы 2.
← разрешающая строка
↑ разрешающий столбец Построение таблицы №2. 1. Заменим переменные в базисе с х3 на х1. 2. Делим элементы разрешающей строки (табл.1) на разрешающий элемент, результаты занесем в строку х1 в табл. №2. 3. В остальных клетках разрешающего столбца (табл. 1) записываем 0. 4. Остальные клетки заполняем по правилу прямоугольника НЭ=СТЭ-(АхВ)/РЭ
СТЭ А
В РЭ
5. Критерий эффективности опять не выполнен, т.к. F имеет два коэффициента - 3 < 0 Построение таблицы №3 Таблицы 3.
Из таблицы 3 видно – критерий оптимальности выполнен. Оптимальные базисные решения Х*=(12, 3,0,0) 7 7 F=5x1-x2=5x 12 - 3 = 57 7 7 7
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ №1
Пример. Решить следующую задачу максимизации F(x)=5x1-x2→max 2x1-x2+x3≤3 3x1+2x2≤6 x1≥0; x2≥0
Запишем систему в каноническом виде 1) 2x1-x2+x3=3 2) 3x1+2x2=6 3) x1=0; x2=0
Решение. В системе координат Х1ОХ2 построим ОДР.
При Х1=0 X2=-3 → (X1,X2)=(0,-3) прямая (1) При Х2=0 Х1= 3 → (X1,X2)=(3, 0) 2 2
При Х1=0 X2=3 → (X1,X2)=(0,3) прямая (2) При Х2=0 Х1=2 → (X1,X2)=(2, 0)
Из условия (3) (Х1, Х2)=(0,0) Х1=0 – прямая (3) Х2=0 – прямая (4)
Для определения с какой стороны прямых ОДР все точки удовлетворяют неравенствам возьмем точку (1,1). Таким образом, ОДР лежит внутри АВСD. Для определения точки выхода, строим прямую: F(x)=5x1-x2=0 5x1=x2→ x1=x2=0 при x1=1, x2=5 Строим нулевую линию уровня целевой функции. Строим нормальный вектор q (5.-1) Передвигая линию уровня целевой функции параллельно себе, по вектору q, фиксируем ее крайнее положение (т.В), которая принадлежит прямым (1) и (2).
2x1-x2+x3=3 3x1+2x2=6
x1= 12 x2= 3, т.е. Х*=(12, 3) 7 7 7 7 F(Х*)=5х 12 - 3 = 57 7 7 7
2.8Двойственные задачи линейного программирования (ДЗЛП). Рассмотрим пример 2.6 и пример 2.5 и представим их в виде таблице
Из таблице видно, что задачи 1 и 2 обладают следующими свойствами: 1) В задаче 1 ищут max, во 2 ищут min. 2) Коэффициенты целевой ф-ции 1-ой задачи являются свободными членами системы ограничения 2-ой задачи. 3) Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида ≤, а в задаче минимизации вида ≥. 4) Матрицы коэффициентов в системе ограничения обеих задач являются транспонированными друг другу.
задачи 1 A1= 2 1 16 0 1 5 3 0 21 2 3 F
Для задачи 2 A’1= 1 2 0 3 2 3 1 1 0 21 18 16 5 21 Z
5) Число неравенств в системе ограничений 1-ой задачи совпадает с числом переменных 2-ой задачи. 6) условие не отрицательности переменных есть в обеих задачах. Две задачи, обладающие указанными свойствами, называются симметричными взаимно – двойственными задачами. 2.9Алгоритм составления двойственных ЗЛП: Исходя из вышесказанного логично предложить следующий алгоритм: 1) Привести все неравенства системы ограничений исходной задачи к одному смыслу: если в исходной задаче ищут max целевой функции, то все неравенства системы ограничений привести к виду ≤, а если ищут min – к виду ≥. Для этого неравенства, в которых это требование не выполняется, умножить на (-1). 2) Составить расширенную матрицу системы A1. 3) Найти матрицу A1, транспонированную к матрице A1. 4) Сформулировать двойственную ЗЛП Этот алгоритм можно проиллюстрировать следующим примером: Составить задачу двойственную следующей задаче: F=14x1+10x2+14x3+11x4→max Система ограничений:
х1+х2+2х3+3х4≤30 3х1+х2+2х3+х4≥40* х1≥0 х2≥0 х3≥0 х4≥0
Решение:
Выполнить самостоятельно: 1. Составить ДЗЛП следующей задачи
При ограничении: 2x1-x2≥1 -x1+4x2≤24 x1 -x2≤3 x1 +x2≥5
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.107 (0.368 с.) |


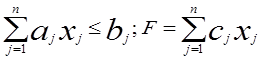
 12x1 + 4x2 ≤ 300
4x1 + 4x2 ≤ 120
3x1 + 12x2 ≤ 252
F = 30x1 + 40x2 → max
12x1 + 4x2 ≤ 300
4x1 + 4x2 ≤ 120
3x1 + 12x2 ≤ 252
F = 30x1 + 40x2 → max
 х1 + 3х2 ≤ 21
х1 + 3х2 ≤ 21 Решение.
Решение. 1) х1 + 3х2 = 21
1) х1 + 3х2 = 21 2) 3х1 + 2х2 = 21
2) 3х1 + 2х2 = 21 3) 3х1 + х2 = 18
3) 3х1 + х2 = 18 х1 + 3х2 = 21 х1 = 3; х2 = 6
х1 + 3х2 = 21 х1 = 3; х2 = 6 (где m-число уравнений, а n-число переменных). Решение системы Х(х1, х2…хn) называется допустимым, если оно содержит лишь неотрицательные компоненты, в противном случае решение называется недопустимым. Базисным решением системы m уравнений с n неизвестными называется решение в котором все (n – m) переменных равны 0. Допустимое базисное решение иначе называется опорным планом.
(где m-число уравнений, а n-число переменных). Решение системы Х(х1, х2…хn) называется допустимым, если оно содержит лишь неотрицательные компоненты, в противном случае решение называется недопустимым. Базисным решением системы m уравнений с n неизвестными называется решение в котором все (n – m) переменных равны 0. Допустимое базисное решение иначе называется опорным планом. х1 – х2 – 2х3 + х4 = 0
х1 – х2 – 2х3 + х4 = 0 - X1X2, X1X3, X1X4, X2X3, X2X4, X3X4.
- X1X2, X1X3, X1X4, X2X3, X2X4, X3X4.
 2.6 Симплекс-метод (СМ) решения ЗЛП
2.6 Симплекс-метод (СМ) решения ЗЛП - если в выражении целевой функции отсутствуют положительные коэффициенты при неосновных переменных, то решение максимально;
- если в выражении целевой функции отсутствуют положительные коэффициенты при неосновных переменных, то решение максимально; y1+2y2+3y4≥2
y1+2y2+3y4≥2 3y1+y2+y3-y6=3
3y1+y2+y3-y6=3

 0 3 ≠0
0 3 ≠0 y1=1- 1 y2 - 1 у3+ 1 у6;
y1=1- 1 y2 - 1 у3+ 1 у6; у1= 4 - 2 у3+ 5 у4- 1 у5+ 2 у6
у1= 4 - 2 у3+ 5 у4- 1 у5+ 2 у6 x1+3x2≤18
x1+3x2≤18 х1+3х2+х3=18
х1+3х2+х3=18




 Из первого уравнения:
Из первого уравнения:
 x1+3x2≤18
2x1+x2≤16
x2≤5
3x1≤21
x1, x2≥0
Составить такой план выпуска продукции X=(x1, х2) при котором прибыль при реализации будет max.
В общем виде задача запишется:
n
F=∑Cjxj→max,
j=1
при ограничениях:
n j=1,2…m
∑aijхi≤ bi i=1,2…n
j=1
x1+3x2≤18
2x1+x2≤16
x2≤5
3x1≤21
x1, x2≥0
Составить такой план выпуска продукции X=(x1, х2) при котором прибыль при реализации будет max.
В общем виде задача запишется:
n
F=∑Cjxj→max,
j=1
при ограничениях:
n j=1,2…m
∑aijхi≤ bi i=1,2…n
j=1
 y1+2y2+3y4≥2
3y1+y2+y3≥3
y1, y2, y3, y4≥0
Найти такой набор цен ресурсов Y=(y1,y2,y3,y4), при котором общие затраты на ресурсы будут минимальны.
В общем виде задачу запишем:
m
Z=∑ biyi →min,
i=1
при ограничениях:
m j=1,2…m
∑ aijyi≤ cj i=1,2…n
i=1
y1+2y2+3y4≥2
3y1+y2+y3≥3
y1, y2, y3, y4≥0
Найти такой набор цен ресурсов Y=(y1,y2,y3,y4), при котором общие затраты на ресурсы будут минимальны.
В общем виде задачу запишем:
m
Z=∑ biyi →min,
i=1
при ограничениях:
m j=1,2…m
∑ aijyi≤ cj i=1,2…n
i=1

 Для 1 3 18
Для 1 3 18 4х1+2х2+2х3+3х4≤35
4х1+2х2+2х3+3х4≤35

 4 1 -3 14
4 1 -3 14
 F=-x1+2x2→max
F=-x1+2x2→max


