
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретизация частных производных.Содержание книги Поиск на нашем сайте
По определению частная производная от функции непрерывного аргумента
. Для функции дискретного аргумента на фиксированной сетке понятие предельного перехода теряет смысл, поэтому при определении разностной производной вместо отношения бесконечно малых величин берут отношения конечных разностей. Аппроксимация производной 1.1 может быть проведена с помощью различных формул: а) правая производная: б) левая производная: в) центральная производная: г) трёхточечная несимметричная: д) пятиточечная симметричная:
Ясно, что при дискретизации производной с помощью любого из выражений 1.2-1.6 вносится ошибка аппроксимации, порядок которой для каждой формулы можно оценить, если воспользоваться разложением в ряд Тейлора соответствующих функций в точке х, так например:
Тогда порядок ошибки аппроксимации с помощью формулы 3.2 для правой производной будет:
Аналогично имеем такой же порядок ошибки аппроксимации и для левой производной 3.3. Для центральной производной получим:
Если всё тоже выполнить для трехточечной несимметричной производной 1.5, то найдем порядок ошибки аппроксимации Основываясь на полученных результатах, о порядке вносимой ошибки за счет дискретизации может показаться, что во всех случаях следует пользоваться более сложной формулой аппроксимации производной. На практике при решении нестационарных задач газовой динамики дискретизация производных по времени чаще осуществляется с использованием правой производной. Это позволяет, зная параметры течения газа на n шаге по времени, определить их на (n+1). Использование в данном случае более сложных формул ограничено незнанием параметров течения на (n+2) шаге по времени. Дискретизацию производных по пространству следует производить с помощью центральной производной 1.4, а не пятиточечной симметричной 1.6, хотя ошибка аппроксимации с помощью последней значительно меньше. Объясняется это тем, что использование в формуле 1.6 большего количества точек приводит к снижению вычислительной эффективности и увеличивает время счета. Точность расчета всегда можно повысить измельчением сетки.
ДИСКРЕТИЗАЦИЯ УРАНЕНИЙ, ОПИСЫВАЮЩИХ ТЕЧЕНИЕ ГАЗА.
При построении разностной схемы для численного решения двумерной по пространству задачи, необходимо ввести также двумерную разностную сетку. Сетка прямоугольная, её линии параллельны завесе. На сетке выбрана система координат OIJ (см. рис. 1.1) таким образом, что I=1 совпадает с проёмом, I=N совпадает с поверхностью завесы, J=0 совпадает с проёмом, J=М совпадает с поверхностью пола. N и M задаются, они определяют число расчетных узлов сетки и шаги (расстояния от узла до узла) вдоль соответственно осей. При дискретизации дифференциальных уравнений и дополнительных условий будем аппроксимировать частные производные по пространству с помощью центральной производной 3.4, 3.10, а частные производные по времени по формуле для правой производной 3.2. Для приведения к одной точности аппроксимации производных по пространству первого и второго порядков будем использовать так называемую разнесенную разностную сетку, в которой различные зависимые параметры определяются в разных точках сетки. В связи с этим, функции непрерывного аргумента
Здесь и ниже величины, обозначенные индексом n+1, являются функциями, определенными на n+1 шаге по времени. Функции, определенные на n – ом шаге по времени, индекса не имеют. 1) ∂T/∂t+U*∂T/∂x+V*∂T/∂y=P/(ρ2*cv)*∂ρ/∂t+ K*Pr/ρ*∂/∂x*((µ+Aτ) *∂T/∂x)+ ∂/∂y*((µ+Aτ) *∂T/∂y) (Tn+1[I;J]-T[I;J])/∆t+(U[I;J]+ U[I+1;J])/2* (T[I+1;J]- T[I-1;J])/(2*∆x)+ (V[I;J]+V[I+1;J])/2*(T[I;J+1]- T[I;J-1])/(2*∆y)=K*Pr/ρ[I;J]*((T[I+1;J]- T[I;J])/∆x*(µ[I+1;J]+ µ[I;J]+Aτ[I+1;J]+ Aτ[I+1;J])/2- (T[I;J]- T[I-1;J])/∆x*(µ[I;J]+ µ[I-1;J]+Aτ[I;J]+ Aτ[I-1;J])/2)/∆x+((T[I;J+1]- T[I;J])/∆y*(µ[I;J+1]+ µ[I;J]+Aτ[I;J+1]+ Aτ[I;J])/2- (T[I;J]- T[I;J-1])/∆y* (µ[I;J]+ µ[I;J-1]+Aτ[I;J]+ Aτ[I;J-1]/2)/∆y; Tn+1[I;J]=(K*Pr/ρ[I;J]*((T[I+1;J]- T[I;J])/∆x*(µ[I+1;J]+ µ[I;J]+Aτ[I+1;J]+ Aτ[I+1;J])/2- (T[I;J]- T[I-1;J])/∆x*(µ[I;J]+ µ[I-1;J]+Aτ[I;J]+ Aτ[I-1;J])/2)/∆x+((T[I;J+1]- T[I;J])/∆y*(µ[I;J+1]+ µ[I;J]+Aτ[I;J+1]+ Aτ[I;J])/2- (T[I;J]- T[I;J-1])/∆y* (µ[I;J]+ µ[I;J-1]+Aτ[I;J]+ Aτ[I;J-1]/2)/∆y-(U[I;J]+ U[I+1;J])/2* (T[I+1;J]- T[I-1;J])/(2*∆x)-(V[I;J]+V[I+1;J])/2*(T[I;J+1]- T[I;J-1])/(2*∆y))* ∆t+T[I;J]. 2) ρ*(∂U/∂t+U*∂U/∂x+V*∂U/∂y= -∂P/∂x+2*∂/∂x*(µ*∂U/∂x)+ ∂/∂y*(µ*(∂U/∂y+∂V/∂x) (ρ[I;J]+ρ[I-1;J])/2*(Un+1[I;J]- U[I;J])/∆t+(ρ[I;J]+ρ[I-1;J])/2*(U[I+1;J]- U[I-1;J])/(2*∆x)+(ρ[I;J]+ρ[I-1;J])/2*(V[I;J]+V[I+1;J]+V[I;J+1]+V[I+1;J+1])/4*(U[I;J+1]- U[I;J-1])/(2*∆y)= -(P[I+1;J]-P[I;J])/∆x+2*(µ[I;J]* (U[I+1;J]- U[I;J])/∆x-µ[I;J]*(U[I;J]- U[I-1;J])/∆x)/∆x+((µ[I;J]+µ[I-1;J]+µ[I-1;J+1]+µ[I;J+1])/4*((U[I;J+1]- U[I;J])/∆y+(V[I;J+1]- V[I-1;J+1])/∆x)-(µ[I;J]+µ[I;J-1]+µ[I-1;J-1]+µ[I-1;J])/4*((U[I;J]- U[I;J-1])/∆y+(V[I;J]- V[I-1;J])/∆x))/∆y; Un+1[I;J]= (-(P[I+1;J]-P[I;J])/∆x+2*(µ[I;J]* (U[I+1;J]- U[I;J])/∆x-µ[I;J]*(U[I;J]- U[I-1;J])/∆x)/∆x+((µ[I;J]+µ[I-1;J]+µ[I-1;J+1]+µ[I;J+1])/4*((U[I;J+1]- U[I;J])/∆y+(V[I;J+1]- V[I-1;J+1])/∆x)-(µ[I;J]+µ[I;J-1]+µ[I-1;J-1]+µ[I-1;J])/4*((U[I;J]- U[I;J-1])/∆y+(V[I;J]- V[I-1;J])/∆x))/∆y-(ρ[I;J]+ρ[I-1;J])/2*(U[I+1;J]- U[I-1;J])/(2*∆x)-(ρ[I;J]+ρ[I-1;J])/2*(V[I;J]+V[I+1;J]+V[I;J+1]+V[I+1;J+1])/4*(U[I;J+1]- U[I;J-1])/(2*∆y))*∆t/(ρ[I;J]+ρ[I-1;J])/2 +U[I;J]. 3) ρ*(∂V/∂t+U*∂V/∂x+V*∂V/∂y= -∂P/∂y+ ∂/∂x*(µ*(∂U/∂y+∂V/∂x)+ 2*∂/∂y*(µ*∂U/∂y) (ρ[I;J]+ρ[I;J-1])/2*(Vn+1[I;J]- V[I;J])/∆t+(ρ[I;J]+ρ[I;J-1])/2*(U[I;J]+U[I+1;J]+U[I;J-1]+U[I+1;J+1])/4*(V[I+1;J]- V[I-1;J])/(2*∆x)+(ρ[I;J]+ρ[I;J-1])/2* V[I;J]*(V[I;J+1]- V[I;J-1])/(2*∆y)= -(P[I;J]-P[I;J-1])/∆y+((µ[I;J]+µ[I+1;J]+µ[I;J-1]+µ[I-1;J])/4*((U[I+1;J]- U[I;J])/∆y+(V[I+1;J]- V[I;J])/∆x)-(µ[I;J]+µ[I;J+1]+µ[I-1;J]+µ[I;J-1])/4*((U[I;J]- U[I-1;J])/∆y+(V[I;J]- V[I-1;J])/∆x))/∆x+2*(µ[I;J]*(V[I;J+1]- V[I;J])/∆y- µ[I;J-1]*(V[I;J]- V[I;J-1])/∆y)/∆y. Vn+1[I;J]=(-(P[I;J]-P[I;J-1])/∆y+((µ[I;J]+µ[I+1;J]+µ[I;J-1]+µ[I-1;J])/4*((U[I+1;J]- U[I;J])/∆y+(V[I+1;J]- V[I;J])/∆x)-(µ[I;J]+µ[I;J+1]+µ[I-1;J]+µ[I;J-1])/4*((U[I;J]- U[I-1;J])/∆y+(V[I;J]- V[I-1;J])/∆x))/∆x+2*(µ[I;J]*(V[I;J+1]- V[I;J])/∆y- µ[I;J-1]*(V[I;J]- V[I;J-1])/∆y)/∆y-(ρ[I;J]+ρ[I;J-1])/2*(U[I;J]+U[I+1;J]+U[I;J-1]+U[I+1;J+1])/4*(V[I+1;J]- V[I-1;J])/(2*∆x)-(ρ[I;J]+ρ[I;J-1])/2* V[I;J]*(V[I;J+1]- V[I;J-1])/(2*∆y))* ∆t /(ρ[I;J]+ρ[I;J-1])/2+V[I;J]. 4) P[I;J]=(divVB[I;J]-divV[I;J]/(2*∆t)+P[I+1;J]/((∆x2)*(ρ[I+1;J]+ρ[I;J]))+P[I–1;J]/((∆x2)*(ρ[I–1;J]+ρ[I;J]))+P[I;J+1]/((∆y2)*(ρ[I;J+1]+ρ[I;J]))+P[I;J-1]/((∆y2)*(ρ[I;J]+ρ[I;J-1])))/(1/((∆x2)* (ρ[I;J]+ρ[I+1;J]))+1/((∆x2)*(ρ[I+1;J]+ρ[I;J]))+1/((∆y2)*(ρ[I;J+1]+ρ[I;J]))+1/((∆y2)*(ρ[I;J]+ ρ[I;J-1]))).
J
Рис. 3.1. Дискретное распределение параметров течения газа на разностной сетке
|
||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 740; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.44.93 (0.006 с.) |

 (1.1)
(1.1) (1.2)
(1.2) ; (1.3)
; (1.3)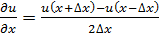 ; (1.4)
; (1.4)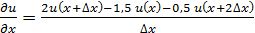 ; (1.5)
; (1.5) (1.6)
(1.6) (1.7)
(1.7)
 (1.8)
(1.8)
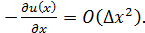 (1.9)
(1.9) , а для пятиточечной симметричной 1.6 -
, а для пятиточечной симметричной 1.6 -  .
. заменяем функциями дискретного аргумента
заменяем функциями дискретного аргумента  , определенными в точках
, определенными в точках  ,
,  - в точках
- в точках  ,
,  - в точках
- в точках  (см. рис. 3.1).
(см. рис. 3.1).






 I
I


