
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Современные методы расчета воздушных завес различного назначения.
В последние годы в инженерной практике используется метод расчета воздушных завес, предложенный В. М. Эльтерманом [11]. Метод В. М. Эльтермана является дальнейшим развитием методов, разработанных В. В. Батуриным, А. Шепелевым, С. Е. Бутаковым. В. М. Эльтерман рассматривает действие воздушной завесы как дополнительное сопротивление, уменьшающее количество воздуха проходящего через ворота, которое характеризуется коэффициентом расхода воздуха: В теоретическом решении В. М. Эльтерман использовал теорему о количестве движения, как это делал Т. Н. Каменев при решении задачи о сопротивлении тройников. Схема действующих сил при работе завесы дана на рис. 1.3.
Рис. 1.3. Схема действующих сил при работе завесы
Разность давления снаружи и внутри здания в воротах, защищенных завесой, расходуется на торможение струи завесы и на придание потоку воздуха, входящего в помещение, скорости в горизонтальном направлении. Это видно из уравнения, полученного В. М. Эльтерманом из условия равенства приращения количества движения за единицу времени и действующих сил:
где: FB, Fщ, F - площадь соответственно ворот; щелей, через которые выходит струя воздушной завесы; плоскости А В; μ - коэффициент расхода воздуха через ворота, защищаемые завесой; ψ - поправочный коэффициент на количество движения учитывающий неравномерность поля скоростей; V см - средняя скорость движения воздуха в сжатом сечении за воротами; Vз - скорость выхода воздуха из щели завесы; ρ з, ρ см - плотности воздуха, выходящего из завесы и при температуре смеси воздуха завесы и наружного воздуха; R c - среднее реактивное давление стены в пределах плоскостей В Г и М α - угол между направлением выхода струи завесы и плоскости ворот; θ - угол между направлением скорости и осью. Решение уравнения c использованием опытных данных дало зависимость между коэффициентом расхода μ и относительным расходом воздуха на завесу в виде:
Или
Относительный расход воздуха завесой равен отношению количества воздуха, подаваемого в завесу Z3 к количеству воздуха, проходящего через ворота
Анализируя формулу В. М. Эльтерман приходит к выводу, что
эффективность действия завесы зависит от
параметра
При прочих равных условиях необходимый расход воздуха на завесу обратно пропорционален корню квадратному из D:
Так как параметр D состоит из трех сомножителей, следует, что
т. е. чем больше относительная площадь щели, тем больше воздуха нужно подавать в завесу для получения того же эффекта; чем больше угол α приближается к 90°, тем меньше расход воздуха на завесу: Кроме того, величина q зависит от соотношения массовой плотности воздуха, подаваемого в завесу, к массовой плотности смеси воздуха завесы с наружным:
Так как ρ з < ρ см, для получения такого же эффекта можно подавать в завесу несколько меньше воздуха (по весу), чем при изотермических условиях (ρ з = ρ см). Но необходимый объем воздуха, подаваемого в завесу, возрастает с увеличением его температуры. Чем больше μ0 тем при прочих равных условиях будет больше коэффициент расхода воздуха при действии завесы. Теоретические выводы В. М. Эльтермана подтверждаются экспериментами. Однако опытные точки ложатся ниже теоретической кривой. С учетом поправок, полученных опытным путем, Эльтерман рекомендует использовать своё уравнение в виде:
где: С - переменный коэффициент, значение которого определяется экспериментально. В. М. Эльтерман рекомендует применять уравнение для рационально устроенных воздушных завес с углом выпуска воздуха α = 30° - 60° в диапазоне изменения относительного расхода воздуха на завесу q= 0,5-1,0. Теоретические выводы В. М. Эльтермана легли в основу инженерного метода расчета воздушных завес, разработанного Сантехпроектом [15, 55]. Методика В. М. Эльтермана дает возможность определить расход воздуха на завесу. Развитие струи, ее траектория в этой работе не рассматривается. Устройство локализующих воздушных завес большим относительным расходом q>0,5 является неэкономичным. Несмотря на очевидные преимущества метода В. М. Эльтермана, он не свободен от недостатков. Последние имеются внутри самого решения и в его результатах. Так, правая часть уравнения, которая содержит величины φ, ξ см, R c была принята равной μ о с определенными допущениями на основании единичного эксперимента. При решение по формуле получается, что при угле наклона струи завесы к плоскости ворот, равном нулю, завеса не оказывает никакого сопротивления проходу воздуха через ворота. Между тем, такой результат не кажется очевидным. Аналитическое решение В. Д. Столера и П. Ф. Аликина [58] подтверждает это.
Методика расчета воздушных завес периодического действия с учетом воздушного режима помещения в целом разработана в МИСИ В.П.Титовым [56, 57]. Чтобы воздушный баланс помещения не изменялся при работе завесы, рекомендуется выдерживать следующие условия: количество воздуха, попадающее со струёй завесы в помещение, должно быть равно количеству воздуха, забираемого завесой из помещения (с учетом подсоса воздуха к струе). Уравнение траектории оси изотермической струи завесы было получено им по методике профессора С. Е. Бутакова [9] с использованием теоремы о количестве движения.
Для вертикальных струй, при направлении оси х вдоль плоскости проема в направлении струи (рис. 1.4) В. П. Титов рекомендует уравнение
Где:
- максимальная разность давлений в проеме;
Δр- разность массовой плотности воздуха внутри и снаружи. Для выполнения предложений рекомендации необходимо, чтобы ось струи завесы прошла через точку имеющую координаты х = Н; у = -r, здесь Н - высота ворот; r - полуширина струи.
Рис 1.4. Схема струи воздушной завесы в проёме наружного ограждения.
Используя известные зависимости по распределению скоростей и расходов в сечениях свободной плоской струи, В. П. Титов получил зависимости величин r от во и х. Скорость на выходе из щели для вертикальной завесы, направленной снизу вверх, предлагается рассчитывать по формуле:
Так как методика расчета воздушных: завес, предложенная В.П.Титовым, построена с учетом воздушного режима помещения, при наличии теплового и ветрового давления, она охватывает широкий круг физических процессов в здании. Однако, использование автором при решении задачи теории свободной турбулентной струи является не вполне оправданным. По данным многих исследователей струя, развивающаяся в сносящем потоке воздуха, отличается по своим свойствам от свободной струи, так как статическое давление в ней неравно давлению окружающего воздуха. Наряду с обычными завесами, в современных горячих цехах применяют циркуляционные завесы с организацией забора воздуха в плоскости ворот. О. Е. Бутаков и В.Д. Столлер [39] предложили аналитическое решение задачи о циркуляционной завесе методом наложения потоков. Поскольку этот метод не учитывает всей динамики процесса, то авторы рассматривают его лишь как первое приближение. Однако полученное решение позволило сделать некоторые предварительные выводы о шиберующей способности циркуляционных завес В. Д. Столер [58] провел также экспериментальные исследования, в которых изучалось влияние отсоса над воротами на шиберующий эффект циркуляционных завес. Опытные данные обрабатывались по методике В. М. Эльтермана [11]. Опыты показали, что зависимости величины коэффициента расхода от q √D при действии циркуляционных завес вполне удовлетворительно описывается формулой.
С. Е. Бутаков и В. Д. Столер установили, что по количеству воздуха, прорывающегося в цех,, при прочих равных условиях, циркуляционные завесы мало чем отличаются от обычных шиберующих завес. Существенное различие лишь в том, что прорывающийся в цех воздух направляется циркуляционной завесой вверх вдоль наружной стены. Это позволяет снизить относительный расход воздуха на завесу. Татарчук Г.Т. [59] провела испытания воздушно-тепловых завес циркуляционного типа на модели. Завесы были выполнены по двум схемам. В первой схеме завесы воздух подавался с одной стороны проема и отсасывался с противоположной. Во второй схеме воздух подавался сверху и отсасывался снизу у пола с двух сторон проема. В обоих случаях воздух подавался под углом 30° к плоскости проема. Было установлено, что более эффективными и экономичными являются циркуляционные завесы с верхней подачей воздуха. Для них коэффициент расхода воздуха через проем ворот имеет наименьшее значение по сравнению с обычными двухсторонними и боковыми циркуляционными завесами. Экспериментальные данные НИИСТ [56] подтверждают экономическую целесообразность применения циркуляционных завес. В настоящее время наибольшее внимание исследованиям проблемы расчета воздушно-тепловых завес уделяли А.С. Стронгин «ОАО «ЦНИИ Промзданий», М.В. Никулин «ООО «НПО ТЕРМЭК» и М.Е Дискин «ООО «Климатвентмаш». По мнению А.С. Стронгина и М.В. Никулина, струя воздушной завесы не является аналогом свободной струи, поэтому задание средней скорости на участке разворота и взаимодействия с ограждениями (или встречной струей при двухсторонней завесе) не характеризует реальную картину течения. Тепло- и массообмен в проеме определяется не геометрическими построениями траектории оси или границ струи, а законами сохранения массы, теплоты и количества движения в зоне проема. Принципиальным условием является соблюдение закона сохранения импульса в зоне проема, включающего наружные ограждения. Подход М.Е. Дискина к подбору воздушных завес строится на следующих факторах. При рационально выполненной завесе сквозь проем проходит только струя завесы. При этом температура воздуха, проходящего через проем, даже в случае прохождения части струи вне проема, будет не ниже значения средней температуры в сечении струи, первым соприкасающимся с ограждением проема. Для проверки выполнения в выбранной завесе условия перекрытия проема строится траектория струи этой завесы, что дает возможность оценить расположение струи относительно проема и принять решение о пригодности выбранной завесы. Задание значения средней скорости воздуха в сечении струи, первым соприкасающимся с ограждением проема (средняя скорость в конце струи), или, что более точно, соотношения средней скорости и скорости в проеме ворот без завесы, позволяет при подборе завесы определить условия формирования траектории струи при воздействии поперечного потока.
Среди различных существующих методов, чтобы характеризовать аэродинамический уплотнительный эффект предоставляемый воздушной завесой расположена над отверстием между двумя смежными отсеками. Инфракрасная термография выявит быть очень полезным инструментом. Помимо, позволяет захвата, в быстром пути, мгновенной фотографии температурного поля в окрестности дверь, техника hereon описано имеет другие преимущества, с точки зрения быстрой и легкой настройки, низкого навязчивого характера и ответственности полученных результатов.
Чтобы применить этот метод, большой лист бумаги был вытянут в направление перпендикулярном к открытию, где устройство воздушных завес поставил, чтобы позволить регистрацию фотографии или видео последовательностей с инфракрасным настройки камеры в ее максимальной чувствительности. Хорошее соответствие между термографами получаемыми с этой техникой и температурные поля которые измеряются в одной плоскости со стойкой из 16 низких скоростей всенаправленными тепловыми датчиками анемометра. Различные примеры использования этой методики в качестве дополнительного инструмента для анализа и визуализации сложных физических явлений, происходящих в исследуемом потоке представлены в этой статье [61].
В работе представлена здесь [61], было можно позволить поведение струи воздушной завесы в плане отклонения прогиб, удара уголя на земле, эволюции запуск переходной фазе, градиентов температуры в исследуемой зоне, Из изображений, собранных с помощью инфракрасной термографии. В случае ACD без рециркуляции, установленных в отсеках, которым можно считаться герметичными относительно внешнего помешения, существует оптимальный импульс струи (минимум), гарантирующий непрерывность завесы до земли и сводит к минимуму теплообмен. Если угол воздействие потока на пол не совпадает с начальным углом струи (a0), Dm пишется следующим образом:
Где
Это оптимальное рабочее условие соответствует минимуму модуля отклонения
В. Титария, А. Тивари [62] провели исследование, показывающее комплексных результатов, которые могут быть использованы для оптимизации и прогнозирования производительности воздушной завесы в помещениях. Параметр исследования в этой статье исследовал, как плотность, скорость и температура воздуха внутри и снаружи воздушной завесы варьируются в зависимости от высоты для различных климатических условий. Результаты получены моделью, разработанной для быстрых вычислений и параметрического анализа для проектирования и калибровки целей холодильного оборудования.
O. Мюллер [63] проводил исследование по программному обеспечению для моделирования вентиляции в центр прикладных исследований в Нидерландах. В этом исследовании, используя воздушные завесы с выпрямителем струи, потери энергии через проем могут быть уменьшены на 94%. Чем ниже выбрана температура струи, тем лучше настройки струи и эксплуатации воздушных завес. Это важно, чтобы приносить немного больше энергии, чем это необходимо для нагрева поступающего воздуха, но испытании показали, что, несмотря на, то что, температура струи выбрана относительно низкой, в помещение получается желаемый комфорт. Предыдущие исследования также показали, что превышение скорости является основной причиной потери энергии и плохого кондиционирования поступающего воздуха. A.M. Фостер, M.J. Сван [64] и другие провели исследование с целью оценить эффективность коммерческие доступные воздушные завесы с различными скоростями струи и найти оптимальную скорость струи, чтобы дать максимальную эффективность. Аналитическая модель Хаеса и Стоецкера была использована для прогнозирования оптимальных скоростей струи для этой завесы и модель В.Г была использована, чтобы обеспечить более глубокое понимание проблемы.
Скорость струи воздушной завесы по ширине канала в среднем 10,5 м/с.. Измеренная эффективность завесы составила 0,2 для открытой двери в момент 10 сек и 0,31 в те 30 сек. Результаты показали важность создания воздушной завесы для обеспечения оптимальной эффективности. Аналитическая модель дает руководство к скорости струи, однако, мы показали, что с конкретной воздушной завесой, эффективность может сильно варьироваться, в зависимости от скорости, которая была выбрана. Аналитическая модель является неспособной в состоянии дать любое руководство по эффективности завесы при различных скоростях струи.
В статье [65] предложена методика, позволяющая формализовать проверочные расчеты и проанализировать полученные результаты. Проиллюстрируем на ряде примеров применение для ВТЗ методики расчета, приведение в [68]. Рекомендуется следующий порядок действий. Эта методика базируется на параметрах f и q, используя таблицы, для того чтобы определить коэффициент динамической эффективности Е для f и q первоначально выбранные. Затем можно рассчитывать воздухопроизводительность воздушно-тепловой завесы:
Где
- Подбирая по каталогам ВТЗ с близким значением
- По этим новым значениям - Вычислить необходимую температуру воздуха, подаваемого завесой.
Коэффициенты - Определять требуемую тепловую мощность завесы:
Где
- Для выбранной завесы рассчитывают температуру смеси воздуха:
- Определять количество воздуха, проходящего внутрь помещения при работе завесы:
Выбранная ВТЗ должна обладать необходимой динамической эффективностью, т.е. импульсом струи, который характеризуется величинами L и f [65].
Для повышения энергоэффективности применяемых ВТЗ необходимо разработать рекомендации по оптимизации их параметрического ряда. Рекомендации позволяют производителям ВТЗ более корректно формировать номенклатуру выпускаемых агрегатов, а проектировщикам облегчат процесс их подбора[65].
Цели и задачи работы.
Разработка проекта ВТЗ произвольного проема, в настоящее время, происходит на основе стандартных инженерных методов, которые основываются на различных эмпирических данных в которых, не учитываются поля скоростей и температур газа, возникающие в проеме при работе завесы. Это приводит к сильному расхождению результатов, полученных с помощью различных методов, а также к ошибкам при оценке эффективности работы спроектированной завесы, а поэтому, часто сводится к завышению энергоемкости завесы с целью создания не обоснованного запаса его мощности (как уже было отмечено ранее). Для получения полной картины аэро и термодинамических процессов в проеме с целью дальнейшей оценки работы ВТЗ можно воспользоваться имеющимися, универсальными гидродинамическими компьютерными программами, такими как Star CD и Fluent. Эти программы позволяют решать достаточно широкий круг задач, но имеют и ряд недостатков. Их универсальность приводит к их громоздкости. Желание расширить круг решаемых задач, усложняет математическую модель и увеличивает время расчета одного варианта. В этих моделях не учитывается специфика работы тепловых завес, например, существенно дозвуковой характер течения, с ощутимой неоднородностью плотности Приведенные доводы позволяют сделать вывод, что для перехода от инженерных методов проектирования работы тепловых завес к инновационным компьютерным методам, необходимо создание специализированных программ расчета, базирующихся на математических моделях на основе фундаментальных положений аэро и термодинамики, учитывающих особенности работы ВТЗ. В связи с этим целью данной работы является: 1. Симуляция проблемы турбулентного течения вязкого газа созданием математической модели, позволяющей рассчитывать поля скорости, давления, температуры и плотности воздуха в проеме в пусковом и установившемся режимах работы тепловой завесы. 2. Создание программы расчета для ПК на алгоритмическом языке «Бейсик», применительно для пакета Вижел Бейсик, традиционно входящего в различные версии программного обеспечения Виндуус. 3. Проведение расчетов для различных вариантов завес, их установки, режимов работы в различных проемах. 4. Разработка и создание экспериментального стенда, методики проведения эксперимента. 5. Проведение экспериментальных исследований с определением полей температур и скоростей для проемов с ТВЗ для последующего сравнения с расчетными вариантами. 6. Анализ полученных расчетных и экспериментальных результатов. ГЛАВА 2. Постановка задачи. 2.1. Постановка задачи. Фундаментальные уравнения, описывающие турбулентное течение вязкого газа и учитывающие локальность и нестационарность выше названных параметров давно известны – это уравнения Рейнольдса, полученные на основе уравнений Навье-Стокса динамики вязкого газа [1, 2]. В основу изучения движения вязкого газа и вывода уравнений Навье-Стокса положены следующие общие допущения [1]: Газ совершенен, т.е. его параметры удовлетворяют закону Клайперона-Менделеева:
2. Течение газа подчиняется обобщенному закону Ньютона о линейной связи между тензором напряжений и тензором скоростей деформаций. 3. Динамический коэффициент вязкости
4. Коэффициенты теплоемкости 5. Коэффициент теплопроводности газа Так как числа Рейнольдса (Re) течения газа в проемах существенно превышают критические значения, то течение газа носит турбулентный характер. Осредненное турбулентное течение газа описывается уравнениями Рейнольдса, которые выводятся при известных допущениях [1, 2]. Турбулентное перемешивание представляет собой перенос из слоя в слой осредненного течения молей газа, в связи с чем, происходит перенос из слоя в слой количества движения, тепла и вещества газа. Согласно гипотезе Буссинеска [1, 2], для турбулентного переноса справедливы законы ламинарного течения газа, записанные для осредненного упорядоченного потока. Кроме этих допущений, при решении нашей задачи, с учетом геометрии проема и вытекающей плоской струи воздуха, для упрощения постановки и решения задачи, следует рассматривать картину течения в плоскости перпендикулярной плоскости проема (плоскости вытекания струи), пренебрегая некоторым искажением картины течения газа в краевых сечениях вблизи стенок проема. С учетом выше записанных допущений, уравнения Рейнольдса динамики турбулентного течения вязкого газа в проекциях на оси плоской прямоугольной системы координат будут иметь вид: -на ось x:
-на ось у:
здесь Чтобы замкнуть систему уравнений, используем уравнение неразрывности течения газа:
и уравнение баланса энергии газа:
Проекции объемной силы на ось х - где
Для наших условий течения воздуха числа Прандтля Pr и
Исходя из условия, что
С учетом выражений (7) и (8) уравнение (6) примет вид:
Где
Таким образом, для определения шести неизвестных параметров течения газа в проеме (полей составляющих вектора скорости течения газа
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 1223; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.136.235 (0.105 с.) |
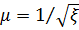 .
.




 величины q и μ0.
величины q и μ0.

 .
.

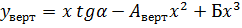








 , по которым есть гарантии, что воздушная завеса стабильно выполняет свою функцию.
, по которым есть гарантии, что воздушная завеса стабильно выполняет свою функцию.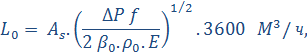
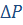 - расчетный перепад давлений в проеме ворот, па;
- расчетный перепад давлений в проеме ворот, па; - коэффициент Буссинеска;
- коэффициент Буссинеска; - плотность воздуха, подаемого завесой.
- плотность воздуха, подаемого завесой. подходящую для данной конструкции ворот, можно определить фактическую воздухопроихводительность
подходящую для данной конструкции ворот, можно определить фактическую воздухопроихводительность  а так же значения
а так же значения 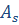 , f и q. Этими данными вычисляется новое значение параметра Е:
, f и q. Этими данными вычисляется новое значение параметра Е:
 и
и  уточнять величену
уточнять величену  по таблице [65].
по таблице [65]. °C,
°C, и
и  принимаются в соответствии с полученными f и q по таблице.
принимаются в соответствии с полученными f и q по таблице. кВт,
кВт, - удельная теплоемкость воздуха, кДж/(кг.град)
- удельная теплоемкость воздуха, кДж/(кг.град)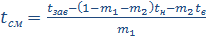 °C,
°C, кг/c,
кг/c, воздуха из-за неоднородности его температуры Т по пространству проема. Не учитывается традиционная простота геометрии проема, вытекание воздуха из аппарата тепловой завесы в виде плоской струи, забор воздуха в аппарат из помещения, в котором установлена тепловая завеса и др.
воздуха из-за неоднородности его температуры Т по пространству проема. Не учитывается традиционная простота геометрии проема, вытекание воздуха из аппарата тепловой завесы в виде плоской струи, забор воздуха в аппарат из помещения, в котором установлена тепловая завеса и др. (1)
(1) является функцией только температуры газа Т и вычисляется по формуле Сатерленда:
является функцией только температуры газа Т и вычисляется по формуле Сатерленда: (2)
(2) и
и  не зависят от абсолютной температуры газа и являются его физическими константами.
не зависят от абсолютной температуры газа и являются его физическими константами. пропорционален динамическому коэффициенту вязкости
пропорционален динамическому коэффициенту вязкости  , в связи с чем число Прандтля Рr =
, в связи с чем число Прандтля Рr =  /
/  рассматривается как физическая постоянная газа.
рассматривается как физическая постоянная газа. (3)
(3)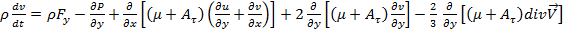 (4)
(4) - составляющая вектора осредненной скорости течения газа вдоль оси
- составляющая вектора осредненной скорости течения газа вдоль оси  ,
,  - составляющая вектора осредненной скорости течения газа вдоль оси
- составляющая вектора осредненной скорости течения газа вдоль оси  ,
,  - давление газа.
- давление газа. (5)
(5) (6)
(6) и
и  в уравнениях (3) и (4) появляются из-за разности плотности газа в различных точках проема вследствие разности температур газа в этих точках – это проекции, так называемой, архимедовой силы. Если ввести коэффициент кубического расширения
в уравнениях (3) и (4) появляются из-за разности плотности газа в различных точках проема вследствие разности температур газа в этих точках – это проекции, так называемой, архимедовой силы. Если ввести коэффициент кубического расширения  , который для совершенного газа равен
, который для совершенного газа равен  , то на частицу газа с температурой
, то на частицу газа с температурой  будет действовать архимедова сила с проекциями на оси координат:
будет действовать архимедова сила с проекциями на оси координат: , на ось у -
, на ось у -  ,
,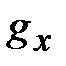 и
и  - проекции вектора ускорения свободного падения на оси координат,
- проекции вектора ускорения свободного падения на оси координат, 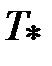 - наименьшая температура на границе расчетной области.
- наименьшая температура на границе расчетной области. в уравнениях (3, 4, 6) – коэффициенты, учитывающие турбулентный перенос количества движения и тепла. Если учесть, что числа Прандтля для ламинарного течения определяется выражением:
в уравнениях (3, 4, 6) – коэффициенты, учитывающие турбулентный перенос количества движения и тепла. Если учесть, что числа Прандтля для ламинарного течения определяется выражением:  а для турбулентного:
а для турбулентного:  то
то 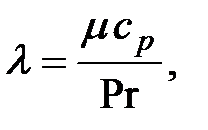 а
а 
 для ламинарного и турбулентного течения близки друг к другу и, примерно, равны единице, тогда правая часть уравнения баланса энергии (6) примет вид:
для ламинарного и турбулентного течения близки друг к другу и, примерно, равны единице, тогда правая часть уравнения баланса энергии (6) примет вид: (7)
(7) , а
, а  , левая часть уравнения (6) может быть преобразована к следующему виду:
, левая часть уравнения (6) может быть преобразована к следующему виду:
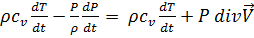 (8)
(8) (9)
(9) .
. - динамический коэффициент турбулентной вязкости может быть определен с помощью одной из существующих моделей, например, универсальной однопараметрической модели А.Н. Секундова [3] для турбулентной вязкости (так же можно использовать и другие модели турбулентности).
- динамический коэффициент турбулентной вязкости может быть определен с помощью одной из существующих моделей, например, универсальной однопараметрической модели А.Н. Секундова [3] для турбулентной вязкости (так же можно использовать и другие модели турбулентности). и
и  , полей температуры Т, плотности
, полей температуры Т, плотности 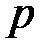 газа и его вязкости
газа и его вязкости  ) составлена система шести уравнений (1, 2, 3, 4, 5, 9). Следовательно, поставленная задача является статически определимой.
) составлена система шести уравнений (1, 2, 3, 4, 5, 9). Следовательно, поставленная задача является статически определимой.


