
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Воздушные струи, развивающиеся при перепаде давлений.Стр 1 из 5Следующая ⇒
Содержание 1.Введение...................................................................................................................2 1.1. Обзор литературы..........................................................................................3 1.1.1. Общие сведения...........................................................................................3 1.1.2. Воздушные струи в сносящем потоке.....................................................5 1.1.3. Воздушные струи, развивающиеся при перепаде давлений............16 1.1.4. Современные методы расчета воздушных завес различного назначения..................................................................................................16 1.2. Цели и задачи работы..................................................................................23 2. Постановка задачи..............................................................................................25 2.1. Постановка задачи.......................................................................................25 2.2. Граничные условия для решения задачи................................................28 2.3 Начальные условия решения задачи.........................................................28 3. Конечно-разностный метод решения задачи течения газа.........................29 3.1 Общие замечания о возможных методах решения задач газовой динамики.........................................................................................................29 3.2. Дискретизация частных производных.....................................................30 3.3. Дискретизация уравнений описывающих течение газа.......................31 3.4. Сходимость и точность разностных схем. Обоснование выбора величины шагов расчета по пространству и времени.........................33 3.5. Создание программы расчета ВТЗ............................................................34 4. Экспериментальное исследование течения воздуха в проеме оборудованном ВТЗ.............................................................................................36 4.1 Методика проведения эксперимента. Экспериментальный стенд......36 4.1.1 Методика проведения эксперимента......................................................36 4.1.2 Экспериментальный стенд.......................................................................37 5. Анадиз полученных результатов......................................................................42 6.Список использованной литературы...............................................................48 Введение. Современный мир невозможно представить себе без огромного количества полезных и удобных устройств, позволяющих человеку обустраивать свою жизнь с комфортом. Тепло–зимой и прохладный и чистый воздух летом – одно из обязательных требований в жизни обычного цивилизованного человека. Тепловые завесы приобретают всё большую популярность в наше время. Основным предназначением таких устройств является защита от холодного воздуха помещений, которые отапливаются. Поток воздуха, который создается тепловой завесой, осуществляет преграду воздух, который попадает в помещение через открытые двери, окна и т.п., тем самым сохраняя теплый воздух внутри помещения.
Воздушные завесы предназначены для разделения внешней среды в помещении. Разделение достигается элиминацией естественной конвекции и нагревом входящего холодного воздуха естественной или принудительной вентиляции. Воздушно-тепловые завесы (ВТЗ) используются для защиты рабочих мест от загрязнения или для уменьшения распространения сигаретного дыма в ресторанах. Первая вертикальная воздушная завеса предположительно была введена в США в 1916 году. Воздушные завесы представляют собой устройства вентиляции локализирующего типа, с помощью которых можно снизить или полностью устранить перемещение воздушных масс через проем, что позволяет уменьшить их вредоносное воздействие на здоровье человека. Воздушная завеса образует плоскую строго направленную струю воздуха, которая помогает избежать потерь тепла, уходящего через проемы открытого типа. Тем самым, воздушные завесы способствуют повышению комфортабельности атмосферы внутри помещения. Для того чтобы системы кондиционирования, вентиляции и отопления могли выполнять поставленные перед ними задачи в полном объеме, поддерживая необходимый микроклимат в помещении, необходимо максимально уменьшить теплопотери путем защиты ограждающих конструкций, в число которых входят открытые дверные и оконные проемы. Дело в том, что при непосредственном контакте окружающей среды с атмосферой помещения неизбежно происходит теплообмен, который оказывает существенное влияние на работу систем вентиляции и кондиционирования, уменьшая экономичность их использования, одновременно повышая энергопотребление. Таким образом тепловой баланс помещения нарушается, как в отдельных тепловых участках, так и по всей кондиционируемой площади. За этот процесс отвечают открытые, свободные или регулярно открываемые окна и двери. Через проем в помещение поступает наружный воздух, имеющий более низкую температуру, нежели внутри помещения. Одновременно с этим, теплый воздух помещения выходит через верхнюю часть открытого проема.
Воздушные завесы являются самым эффективным методом борьбы с теплопотерями. Климатическое устройство монтируется над необходимыми проемами горизонтально, либо сбоку проемов вертикально. Плоская направленная струя воздуха помогает разделить внешнее и внутреннее пространство на разные зоны. Таким образом, воздушная завеса превращается в воздушный экран или виртуальную дверь, создавая защиту помещения от внешнего воздействия. Правильно подобранные и установленные завесы сокращают потери тепла в помещениях до 90%, препятствуя возникновению сквозняков и попаданию снега зимой, а также пыли, пуха, насекомых летом. Завесы с нагревательными элементами позволяют компенсировать потери тепла и поддерживать комфортную температуру в помещениях в холодное время года. Эффективность работы завес определяется: - скоростью воздушной струи по всей высоте защищаемого проема при установке завесы над проемом или по всей ширине проема при боко вом монтаже; - мощностью нагрева приточной струи, компенсирующей теплопотери через открытый проем.
Подбираются данные тепловые завесы соответственно по высоте и ширине дверного проема, который будет защищен от холодного воздуха. Считается, что основными параметрами завесы является ее длина и производительность теплого воздуха. Например, длина воздушной завесы должна быть одинакова или немного больше ширины дверного проема, потому что только в этом случае теплый поток воздуха будет полностью перекрывать поток холодного, тем самым защищая его проникновение вовнутрь. Например, в случае, когда дверной проем составляет в ширину больше, чем 3 метра, то лучше установить несколько тепловых завес. Следует помнить, что чем выше дверной проем, тем мощнее должна быть завеса, и производить больше воздуха. Рекомендуется для защиты маленьких окон киосков, касс использовать завесы производительностью 300 м3/час. Очень важно правильно выбрать тип завесы для создания оптимальной эффективности и комфорта. Воздушная завеса с малой прокачкой воздуха не отсекает сквозняки у пола. Чрезмерно мощная завеса установленная над низкими дверными проемами вызывает чувство дискомфорта у людей под нею и создает повышенную шумность работы. Наилучший результат достигается при перекрытии всей протяженности дверного проема мощным устойчивым потоком воздуха. Завесы могут быть с воздухонагревательной секцией и без нее. Завесы без подогрева устраняют теплопотери так же эффективно, как и завесы с подогревом, однако в некоторых случаях следует учитывать, что не подогретый воздушный поток может вызвать ощущение сквозняка. Дополнительный подогрев воздуха придает комфорт в ощущениях и удовлетворяет потребность в дополнительном тепле к существующему обогреву помещения, осушает пространство, примыкающее к входным дверям.
Производительность по воздуху является основным параметром любой завесы. От производительности зависит скорость воздушного потока и, соответственно, оптимальная высота установки завесы. Например, для защиты стандартного дверного проема шириной 0,8-1,0 метр и высотой 2,0-2,2 метра требуется завеса с производительностью 700-900 м3/ч. В этом случае скорость воздушного потока на выходе завесы составит 6-8 м/с, а на уровне пола - 1,5 - 2,0 м/с. Если установить завесу меньшей производительности через нижнюю часть дверного проема будет проникать холодный воздух, и желаемый эффект от тепловой завесы будет достигнут лишь частично. Заметим, что при наличии тамбура применение завесы с низкой производительностью может быть вполне оправдано – двойные двери создают дополнительную преграду холодному воздуху и позволяют использовать менее дорогую завесу. Тепловые завесы имеют длину от 600 до 2000 мм. Наибольшее распространение получили аппараты длиной 800-1000 мм, предназначенные для установки над стандартными дверными проемами. Длина подобранной завесы должна быть равна или немного больше ширины проема, так как только в этом случае поток воздуха будет целиком его перекрывать и не даст холодному воздуху попасть внутрь. Если проем очень широкий (более 2 метров), то следует устанавливать несколько аппаратов вплотную друг к другу. Помимо отсечения наружного воздуха, тепловая завеса может так же нагревать воздух в помещении. Для ориентировочных расчетов можно принять, что для обогрева 10 м2 не отапливаемого помещения, при высоте потолков 2,8 - 3,0 м необходим 1 кВт мощности. При этом считается, что стены и потолок помещения имеют хорошую теплоизоляцию (капитальное здание), поскольку обогреть временное сооружение (железный ларек, ангар) практически невозможно — тепло будет уходить через тонкие стенки. Если же завесу предполагается устанавливать в хорошо отапливаемом помещении, то функция нагрева не обязательна, и можно выбрать модель с минимальной мощностью или, так называемую, воздушную завесу — без функции обогрева. Заметим, что защитные свойства воздушного потока определяются только скоростью воздуха и никак не связаны с его температурой, поэтому мощность завесы является дополнительной, а не основной характеристикой.
У всех завес с функцией обогрева есть одна особенность – на выходе даже очень мощной завесы воздух будет только теплым и никогда – горячим. Это объясняется высокой скоростью обдува нагревательных элементов, поэтому тепловую завесу нельзя сравнивать с тепловой пушкой или тепловентилятором, где скорость обдува в несколько раз ниже, а температура воздуха соответственно, выше.
Большинство тепловых завес предназначено для горизонтальной установки сверху открытого проема. Однако бывает, что такая установка невозможна или нецелесообразна. В этих случаях применяется вертикальная тепловая завеса, которая устанавливается сбоку от проема. Соответственно, воздушный поток от вертикальной завесы будет направлен горизонтально. Высота (длина) вертикальной завесы должна быть не менее 3/4 высоты защищаемого проема. В остальном, вертикальная тепловая завеса ничем не отличаются от горизонтальной. Любая тепловая завеса имеет, как минимум, два переключателя — один включает вентилятор, второй — нагревательные элементы. В дополнении к этому, некоторые завесы имеют двух- или трехступенчатые регуляторы мощности нагрева и двухскоростные вентиляторы. Пульт управления может быть как встроенным, так и выносным (проводным). Встроенные пульты используются только на небольших завесах для стандартных дверных и оконных проемов, иначе до кнопок будет трудно достать. Выносные пульты используются с полупромышленными и промышленными завесами — такой пульт можно установить в любом удобном месте. В дополнении к пульту можно установить термостат, который будет отключать нагревательные элементы (или всю завесу) при достижении заданной температуры в помещении. Помимо моделей с электрическим подогревом, существуют завесы с подводом воды — водяные тепловые завесы. Как следует из названия, источником тепла в таких завесах является горячая вода, которая подается из системы центрального отопления. Повышенная сложность монтажа водяных завес компенсируется низкими накладными расходами при эксплуатации и высокой мощностью. Такие завесы обычно применяют в промышленных зданиях с большими открытыми проемами.
Глава 1. 1.1. Обзор литературы. 1.1.1. Общие сведения.
Методы расчета воздушных завес разрабатывались российскими учеными начиная с 1936 года. Первоначально расчет воздушных завес базировался на определении траектории оси струи воздушной завесы, этот метод совершенствовался Г. Н. Абрамовичем, И. А. Шепелевым, В. В. Батуриным, С. Е. Бутаковым. Во всех этих методах не учитывались характеристики герметичности здания. Кроме того, критерием шиберирующих свойств завесы являлось условие пересечения осью струи завесы плоскости ворот на расстоянии от выхода из щели завесы, равном ширине перекрываемого проема. Наибольшее распространение получил метод расчета воздушных завес, в котором расход воздуха завесы определяется с учетом ветровой нагрузки и степени герметичности защищаемого помещения. Этот метод представлен в "Справочнике проектировщика. Ч. 3. Вентиляция и кондиционирование воздуха" [67].
Размеры воздушной завесы базируется на балансе между сносящим потоком струи и разницей давления в дверном проеме. Есть также некоторые факты, которые должны быть соблюдены, например, расположения рабочих мест по отношению к дверному проему, распространение пыли, допустимый уровень шума, максимальный расход и пространство установки. Давление в проемах зависит от разницы температур между внутренним и наружным воздухом, герметичность оболочки здания, расположение и размер пути утечки. Разница температур создает распределение давления по всему фасаду здания [66].
По предложению Ф.Г. Проскуры [21] ВТЗ начали использоваться в угольной промышленности для борьбы с пылью, образующейся при загрузке угля в скипы. В вентиляционной практике воздушно-струйные укрытия начали применяться для локализации вредных выделений от технологического оборудования (передувки над промышленными ваннами, завесы у проемов термических печей, у сушилок и т.п.). Однако наибольшее распространение воздушные завесы нашли для борьбы с холодным воздухом, проникающим через проемы ворот и дверей в зимний период года. Поэтому большинство теоретических и экспериментальных работ посвящено изучению данного типа завес.
Струя воздушной завесы развивается в поперечном потоке газов или воздуха. Развитие струи в сносящем потоке давно привлекает к себе внимание исследователей. Такого рода течения широко известны в технике: различные завесы, камеры сгорания газовых турбин, дутье в топках паровых котлов, распространение дыма из труб, газовые горелки и т.д. В основе изучения всех этих явлений лежат теории струйных течений - свободной затопленной струи, изотермических струй, струи воздуха, распространяющейся в сносящем потоке. Наиболее изученным видом турбулентных струй является свободная, затопленная струя [22, 23, 24, 25, 26, 27]. В настоящее время известно несколько теорий свободной турбулентности: теория Прандтля, теория Тейлора, новая теория Прандтля, теория Рейхарда, Маттиоли и других авторов. На основе существующих теорий свободной турбулентности и с их помощью профессор Г. Н. Абрамович [23] разработал теорию свободных струй. Е. И. Поляков [28] высказал предположение, что начальная турбулентность не влияет на характер распространения свободной струи и установил, что в основном участке наблюдается один и тот же угол расширения струи, независимо от конструкции насадки, из которой происходит истечение. На характер изменения скорости свободной струи непосредственно влияет только кинематический импульс струи, который зависит от формы начального профиля поля скоростей. Экспериментальные данные подтвердили предположение о том, что абсолютные значения кинематических и энергетических характеристик струи зависят только от количества движения струи при выходе ее из насадки. Это положение учтено в новой теории свободных турбулентных струй Г. Н. Абрамовича [29, 22] и в работах В. Н. Талиева [27]. Решение многих задач вентиляции (воздушное отопление, аэрация и др.) связано с закономерностями развития неизотермических струй. Первая попытка определения траектории неизотермической струи была сделана В. В. Батуриным и И.А. Шепелевым [5]. В их работе установлено, что искривление неизотермической струи зависит от критерия Архимеда. Для определения траектории оси струи использовались кинематические решения. В результате графического сложения векторов скоростей потока ветра, входящего в ворота и векторов средних скоростей вдоль оси струи воздушной завесы В. В. Батурин и И. А. Шепелев получили уравнение изогнутой оси струи воздушной завесы. С. С. Сыркин и Д. H. Ляховский [30] экспериментально исследовали формы струи подогретого воздуха, вытекающего в воздух нормальной температуры. Результаты опытов дали значительное отклонение от теоретического решения В. В. Батурина и И.А. Шепелева. Г. Н. Абрамович, используя экспериментальные данные [31], разработал теоретический метод расчета формы искривленной струи для горизонтального истечения, позже уравнение траектории струи в более общем виде было дано И. А. Шепелевым [32]. Затем И. А. Шепелев [33] аналитически получил основные расчетные зависимости для свободных неизотермических струй различной формы: осесимметричной, плоской и веерной. Теория И. А. Шепелева дает хорошую сходимость для фонтанов, в тоже время значения осевой скорости и избыточной температуры в ряде случаев значительно отличаются от опытных данных. Аналитические формулы для расчета траектории неизометрической струи получены также В. Н. Талиевым [34] и В. С. Омельчуком [35] и дают близкие результаты. Теоретические и экспериментальные исследования по воздушным завесам можно подразделить на две группы: · работы, где изучается траектория воздушной струи; · работы, рассматривающие завесу как шибер, уменьшающий количество проходящего через проем воздуха.
1.1.2. Воздушные струи в сносящем потоке Взаимодействие струи со сносящим потоком весьма сложно. При истечении струи в сносящий поток под некоторым углом к последнему, ось струи под действием сносящего потока искривляется в сторону движения воздуха. Г. С. Шандоров [36] непосредственным измерением установил, что перед газовой струей в сносящем потоке и в лобовой части самой струи имеется зона повышенного статического давления, а в кормовой части струи и за струёй - зона разрежения. Разница давлений по обе стороны струи является физической причиной искривления ее траектории. Форма поперечного сечения круглой струи под действием сносящего потока деформируется и становится подковообразной. Это объясняется тем, что периферийные слои струи, имеющие малую скорость и интенсивно сдуваемые воздухом, имеют большую кривизну траектории, чем основная масса струи. Характер взаимодействия между струей и сносящим потоком таков, что за струей и в самой струе имеются вторичные вихревые течения. В результате процесс перемешивания газа с воздухом в такой струе должен происходить значительно интенсивнее, чем в струе, вытекающей в неподвижную среду. Однако в [37] на основе измерений в нескольких нормальных сечениях струи установлено, что масса струи, развивающейся в поперечном потоке, изменяется примерно так же, как и у свободной. Траектории распространения струй в сносящем потоке наиболее полно исследованы в работах Ю. В. Иванова [38]. Им исследованы траектории одиночной круглой, плоской и прямоугольной струй в свободном поперечном и ограниченном потоке, а также траектории круглых и прямоугольных струй, размещенных в ряд, в поперечном ограниченном поле. Для создания плоской струи использовались сопла с шириной 0,9; 2,7; 4,0 мм. Опыты проводились при двух значениях отношения абсолютных температур Т2/ T1=1 и 2. При этом отношения кинетических энергий струи и сносящего потока изменялись в широких пределах от 400 до 12,5. Опыты проводились с соплами, ориентированными под углом а=0° и а=30°. Схема развития струи дана на рис. 1.1.
Рис. 1.1. Схема развития струи в поперечном потоке
В результате обработки опытных данных Ю. Б. Ивановым предложено уравнение для расчета плоской струи в сносящем потоке:
где во - полуширина сопла; у - расстояние от оси сопла по нормали к сносящему потоку; х - расстояние от оси сопла по направлению сносящего потока; v, wo - скорости истечения газа и сносящего потока; p, ро - плотности газа и сносящего потока; а - коэффициент структуры струи; q - гидродинамический параметр, равный отношению кинетических энергий струи и потока. В качестве оси струи Ю. В. Иванов принимал линию, соединяющую точки с максимальными значениями скоростей. В 1965 г. С. Е. Бутаков и В. Д. Столер [39] поставили специальный эксперимент для проверки принимаемого многими авторами допущения о постоянстве количества движения в поперечных сечениях турбулентных струй. Результаты показали, что количество движения в струе, истекающей из круглого отверстия в сносящий поток, остается постоянным, но всегда составляет величину меньшую, чем при отсутствии сносящего потока, и тем меньше, чем больше угол наклона струи к потоку и скорость сносящего потока. И. Б. Палатник и Д. Ж. Темирбаев провели подробное исследование закономерностей распространения осесимметричной воздушной струи в сносящем потоке. В аналитическом решении траектория струи определена путем составления баланса сил на выделенный элемент струи. Окончательное уравнение траектории струи имеет сложный вид и вычисления ее проводились численным методом. Экспериментальное изучение структуры течения, особенностей данного вида струйного движения, закономерностей поля сил, действующих на струю как при изотермическом, так и при не изотермическом течении, отражено в работе [40]. Для d= 20 мм, а = 90° и q = 0,17*0,04 получена следующая формула для траектории струи:
Траекторией струи авторы работы считали геометрическое место точек, являющихся центрами импульсов в каждом сечения струи. В этих экспериментах установлено, что массовый расход в струе в сносящем потоке растет в несколько раз быстрее, чем в струе, вытекающей в неподвижную среду. Достоверность такого результата подкрепляется тем, что проведенные измерения показали постоянство избыточного теплосодержания в разных поперечных сечениях струи. Уровень турбулентности в такой струе оказался значительно выше, чем в свободной затопленной струе и в месте наибольшей кривизны траектории достигал 35%. Всякая турбулентная струя, истекающая вблизи какой-либо поверхности, будет испытывать влияние этой поверхности. Это явление, вошедшее техническую литературу под названием "эффект Коанда" играет важную роль при изучении искривления струй газа. Первые попытки теоретического обоснования этого явления были сделаны в 1960 г. С. Буркви и В. Ньюманом. В основу расчета были положены следующие предпосылки: давление внутри циркуляционной зоны распределяется равномерно, осевая линии струи изгибается по дуге окружности радиусом R, ширина струи мала по сравнению с радиусом R, распределение скоростей в изогнутой струе происходит по аналогии со свободной струей, количество движения в струе сохраняется постоянным. В результате авторы исследования получили уравнение для определения основных параметров струи, развивающейся вблизи плоской поверхности. Так, расстояние вдоль плоской струи до точки деления потока на прямой и обратный определяется по следующей зависимости:
Угол наклона струи при встрече с плоской поверхностью:
Или:
Где
Г. Н. Абрамович [23] получил уравнение оси струи, основанное на сложении вектора скорости потока с вектором средней скорости в данном сечении струи. Работа Г. Н. Уфимцева, Ж Б. Белотелова [8] сводилась к определению изогнутой оси струи с помощью теории В. В. Батурина и И. А. Шепелева. Позднее И. А. Шепелев [66] предложил новый метод расчета завес, также основанный на использовании принципа наложения потоков. В этом методе для нахождения уравнения траектории оси складывались функции тока струи и сносящего потока, при этом считалось, что статическое давление в струе остается постоянным. И. А. Шепелевым были получены формулы, с помощью которых можно определить количество воздуха, поступающего в помещение при действии завесы. Однако, вышеуказанный метод решения справедлив для идеальных жидкостей, т.е. тогда когда при взаимодействии потоков не учитывается влияние вязкости воздуха. Поэтому, предлагаемые аналитические выражения имеют значительную погрешность по сравнению экспериментальными данными. В дальнейшем большое распространение получили динамические методы решения. Г. Н. Абрамович [6] использовал схему, предложенную М. С. Волынским [41], по которой кривизна струи определялась из условия уравновешивания силы, вызываемой разностью давлений на передней и задней стенке струи, центробежной силой. Приняв форму струи в виде эллипса, а коэффициент расширения струи таким же, как прямоугольной струи, Г. С. Абрамович получил следующее уравнение для оси струи:
Где:
Сn - коэффициент силы, зависящей от формы крыла. Для определения оси плоской струи в сносящем потоке им предложено выражение:
Коэффициент С п, Г. Н. Абрамович рекомендовал определять, из сопоставления теоретической кривой с опытными данными. Экспериментальные исследования [31] показали, что на величину коэффициента сопротивления С п при обтекании струи воздушным потоком оказывает влияние перепад статического давления вокруг струи. Вахламов [42] получил уравнение оси струи, используя уравнение количества движения при взаимодействии струй с потоком в проекциях на оси координат. Хотя в процессе решения принимаются довольно грубые допущения, теоретические данные хорошо согласуются с опытными для осесимметричной струи. Т.А. Гиршович [43] удалось найти теоретически не только форму оси плоской струи, но также ее границы и профиля скоростей в различных поперечных сечениях. Задача решалась в криволинейной системе координат, ось абсцисс которой совмещена с осью струи, а ось ординат - нормаль к ней. В этой системе координат записаны уравнения пограничного слоя для зоны смешения с учетом поля давлений, создаваемого центробежными силами и переменной скорости. Для определения внешней границы струи (со стороны набегающего потока) последняя рассматривалась условно как граничная поверхность тока, полученная от сложения набегающего потенциального потока с системой источников, расположенной на линии, параллельной набегающему потоку и проходящей через начало струи. Причем, распределение источников подбиралось из дополнительного условия, сводящегося к тому, чтобы давление на границе струи набегающего потока были одинаковыми. Т. А. Гиршович было проведено также экспериментальное исследование основного и начального участка струи в сносящем потоке. При изучении основного участка рассматривалась струя, выходящая из сопла шириной 1,5 мм. и длиной 300 мм. Сносящий поток создавался аэродинамической трубой диаметром 44 мм. Сравнение Т. А. Гиршович теоретического решения с экспериментальным показало, что ось струи, рассчитанная аналитически, не совпадает с опытными данными. В работе [44] также предложены теоретические зависимости для расчета развивающейся в попутном потоке веерной струи. В 1973 г. Т. А. Гиршович [45] предложила при расчете параметров плоской турбулентной струи в сносящем потеке учитывать величину разряжения за струёй как некоторую эмпирическую константу. На основе экспериментальных данных она установила, что величина разряжения в сносящем потоке за струей постоянна и равна:
Е. В. Ржевский и В. А. Костерин [44] провели исследование распространения веерных и парных плоских струй в поперечном потоке, основанное на взаимодействии сил, воздействующих на элементарный участок струи. Они экспериментально подтвердили, что форма оси веерной и парных плоских струй в сносящем потоке зависит от гидродинамического параметра. Для веерной струи при β = 90° и q = 14-65 было получено:
Опыты показали, что веерная струя отклоняется сильнее, чем одиночная плоская. Н. И. Акатнов [26] предложил ещё один способ теоретического решения задачи о развитии круглой турбулентной струи в поперечном потоке. Он находил изменение количества движения, которое происходит под действием профильного сопротивления и сопротивления «стока», возникающего вследствие того, что условная граница струи является проницаемой. Полученные им уравнения оси струи и распределение максимальных скоростей вдоль оси струи дают удовлетворительной совпадение с опытами Иванова. Я. М. Визель и Й. Д. Мостинский [46], по аналогии с работой Г. Н. Абрамовича, рассматривали в своих аналитических решениях струю как крыло, на которое действует сила набегающего потока. Авторы определили форму оси плоской струи исходя из величины лобового сопротивления, которое струя оказывает потоку:
где; Сх - коэффициент лобового сопротивления струи сносящему потоку. Сравнение с опытными данными показало, что при Сх = 5 и β = П/2 отклонение опытов от теоретической кривой достигает ± 20% (рис. 1.2). Такое расхождение получено и для круглой струи в сносящем потоке.
Рис. 1.2. Траектории струи.
И. А. Шепелев [32] сделал попытку определить форму оси струи независимо от формы приточного отверстия, вычислив величину действующих сил в направлении координатных осей. Он связал их с приращением расстояния dx и dy. Полученное им уравнение оси струи, вытекающей из отверстия произвольной формы под произвольным углом к сносящему потоку, имеет вид:
где: в, l - размеры сопла вдоль, и поперек сносящего потека (ось х направлена навстречу сносящему потоку, ось z- вертикально вверх). Коэффициент аэродинамического сопротивления струи С И. А, Шепелев рекомендует принимать равным 5. В работе Н. М. Соколовой [47] посвященной исследованию вертикальных воздушных фонтанов, распространяющихся в сносящем потоке, используется схема решения И. А. Шепелева. Для установления связи между силами, воздействующими на воздушный фонтан, и перемещениями, Н. М. Соколова рассматривала уравнения количества движения, составленные в проекциях на оси координат. Получены общие формулы, определяющие координаты оси сносимого компактного плоского воздушного фонтанов. Для сносимой изотермической струи, истекающей из щелевидного отверстия, формула имеет вид:
где: Кn – постоянный множитель; Подобное уравнение получено также Я. М. Визелем, И, Л. Мостинским [19]. Значение численного множителя Кn = 2,85. Г. С. Шандоров [37], приняв за основу условие равновесия между аэродинамической силой, изгибающей струю и центробежной силой, действующей на элемент струи, вывел уравнение, связывающее координаты оси струи:
Проведенные им эксперименты со струёй, втекающей в поток под углом 60°, с отношением динамического давления потока и струи q = 0,0403 - 0,4 и постоянной Сn = 4,7, показали удовлетворительное совпадение с уравнением. А. М. Эпштейн [48], пользуясь теоретическими разработками Г. Н. Абрамовича [6], получил уравнение оси сносимой неизотермической струи:
где: п - экспериментальная постоянная; Ач - критерий Архимеда. И. В. Календайте и М. Я. Залишаускас получили уравнение траектории плоской свободней струи при разных давлениях с двух сторон [49]:
где: k - безразмерный коэффициент. Метод расчета деформации осей двойных плоскопараллельных струй с учетом перепада статического давления на участке сближения был предложен в 1966 г. Б. Г. Худенко [50]. Также как и в [51] Б. Г. Худенко предполагал, что турбулентные пульсации не проникают в пространство между струями, движение воздуха в этой области носит потенциальный характер и происходит без потерь полного давления. Для аналитического выражения профиля скоростей им была принята формула Г. Шлихтинга. Коэффициент разряжения между струями выражается для начального участка:
для основного: участка:
где: А2 - теоретическая константа; ао - экспериментальная константа;
Согласно [29], значения остальных констант могут быть приняты φ1 = 0,981; φ2 = -2,04; А1=0,45; φгр = 2,412. Координаты оси изогнутой газовой струи
Влиянием эжекции воздуха из межструйного пространства пренебрегалось и считалось, что оси смешивающихся струй распространяются прямолинейно. Повышение статического давления на участке смешения струй в расчетах не учитывалось. В 1968 г. К. Форстер, А. К. Мисро и Д. Г. Митчел при расчете налипающей на плоскую поверхность струи предложили учитывать влияние зоны повышенного статического давления, возникающей в месте столкновения струи с поверхностью. В отличие от известной работы, они предложили в уравнение количества движения изогнутой струи, на участке приближения ее к поверхности, вместо величины атмосферного давления учитывать среднюю величину повышенного статического давления. В 1970 г. В. А. Арутюнов и Ю. М. Перепелкин.[52], используя теоретические разработки [37], и применив для описания распределения скоростей в плоской налипающей на поверхность струе формулу Г. Шлихтинга для слоя конечной толщины, получили уравнение длины зоны циркуляции, образующейся при налипании плоской струи на поверхность:
Где:
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 1071; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.20.238.187 (0.182 с.) |



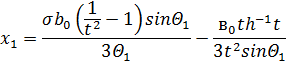



 - постоянная величина
- постоянная величина

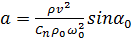










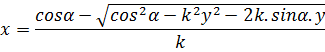

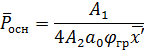
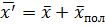 - относительной расстояние сечения от полюса струи.
- относительной расстояние сечения от полюса струи.





