
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Координатное представление векторовСодержание книги
Поиск на нашем сайте
Пусть мы имеем прямоугольную систему координат в пространстве. Если вместе с вектором Обозначим единичные векторы (орты) осей Ox, Oy, Oz соответственно через Разложим произвольный вектор
Рис. 1.7 Векторы Координаты точек Можно сказать, что координатами вектора Составляющие вектора можно выразить через его проекции (координаты):
Подставляя эти значения в равенство
Равенство (1.4.1) можно записать в виде:
Замечание 1. Равные векторы имеют одинаковые координаты. Замечание 2. Разложение вектора Из единственности разложения (1.4.1) вектора Вектор
Рис. 1.8 Поэтому
Из рис. 1.9 видно, что
Рис. 1.9 Используя свойства проекций (п.1.2.), имеем: Разложение вектора
Тройка векторов Замечание. Разложение вектора 1.5. Операции над векторами, заданными Если векторы заданы в координатной форме, то операции сложения и вычитания векторов, умножения вектора на число можно заменить более простыми арифметическими операциями над координатами этих векторов по следующим правилам. Правило 1. При сложении векторов их одноименные координаты складываются:
Правило 2. Чтобы вычесть из вектора
Правило 3. Чтобы умножить вектор
|
|||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.37.85 (0.006 с.) |

 , имеющим произвольную длину, рассмотреть вектор, имеющий единичную длину, но направленный так же, как вектор
, имеющим произвольную длину, рассмотреть вектор, имеющий единичную длину, но направленный так же, как вектор 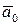 . Отсюда следует, что
. Отсюда следует, что  .
.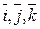 причем
причем  .
. трехмерного пространства по ортам. Для этого построим вектор
трехмерного пространства по ортам. Для этого построим вектор  , равный вектору
, равный вектору  построим прямоугольник ОАММ3, диагональю которого будет вектор
построим прямоугольник ОАММ3, диагональю которого будет вектор  или
или  .
.
 ,
,  ,
,  называются составляющими вектора
называются составляющими вектора  являются координатами вектора.
являются координатами вектора.
 (1.4.1)
(1.4.1) (1.4.2)
(1.4.2)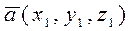 и
и 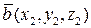 равны, т.е.
равны, т.е.  , то эти векторы тоже равны.
, то эти векторы тоже равны. называется радиус - вектором этой точки, и его координаты совпадают с соответствующими координатами точки
называется радиус - вектором этой точки, и его координаты совпадают с соответствующими координатами точки  (рис. 1.8)
(рис. 1.8)
 , или
, или  . Пусть
. Пусть  - вектор, координаты начала и конца которого известны
- вектор, координаты начала и конца которого известны  и
и  . Тогда координаты вектора
. Тогда координаты вектора  выражаются по формулам:
выражаются по формулам: (1.4.3)
(1.4.3) (1.4.4)
(1.4.4)
 , и аналогичным образом находим
, и аналогичным образом находим  .
. по ортам будет иметь следующий вид:
по ортам будет иметь следующий вид: (1.4.5)
(1.4.5)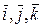 называется координатным базисом, а разложение (1.4.1) вектора
называется координатным базисом, а разложение (1.4.1) вектора  имеет вид
имеет вид  .
. ,
,  ,
, (1.5.1)
(1.5.1)
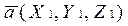 вектор
вектор  , нужно вычест координаты вектора
, нужно вычест координаты вектора  из соответствующих координат вектора
из соответствующих координат вектора 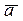 , т.е.
, т.е. или
или  (1.5.2)
(1.5.2) , нужно умножить на это число его координаты, т.е. если
, нужно умножить на это число его координаты, т.е. если  , то
, то  .
.


