
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства смешанного произведенияСодержание книги
Поиск на нашем сайте
1. Смешанное произведение не изменяется: а). Если перемножаемые вектора переставлять в круговом порядке:
б). Если поменять местами знаки векторного и скалярного умножения:
Это позволяет записывать смешанное произведение трех векторов в виде 2. Перестановка в смешанном произведении любых двух векторов изменяет лишь его знак:
Действительно, используя равенства
имеем:
3. Смешанное произведение обращается в нуль, если: а). Хотя бы один из перемножаемых векторов ест нуль - вектор, б). Два из перемножаемых векторов коллинеарны, в). Три перемножаемых вектора компланарны. Координатная форма записи смешанного произведения Коротко смешанное произведение записывается в виде определителя третьего порядка:
Замечание 1. При помощи смешанного произведения можно вычислить объем четырехгранной пирамиды, заданной координатами ее вершин:
Замечание 2. Три вектора
Двойное векторное произведение трех векторов Двойным векторным произведением трех векторов называется произведение вида:
Так как оно часто используется в приложениях, покажем, что его вычисление можно свести к вычислению более простого выражения, т.е. справедливы следующие равенства:
Прежде всего отметим, что двойное векторное произведение трех векторов
Вопросы для самопроверки 1. Дайте определение понятия вектора. 2. Какие векторы называются коллинеарными, компланарными? 3. Основные операции над векторами. 4. Что называется проекцией вектора на заданную ось? Свойство проекций. 5. Дайте определение декартовой прямоугольной системы координат. Векторы в декартовой системе координат. 6. Какая система координат называется полярной? Связь прямоугольных и полярных координат. 7. Запишите операции сложения и умножения вектора на число в координатной форме. 8. Скалярное произведение двух векторов. Определение. 9. Свойства скалярного произведения. 10. Координатная форма записи скалярного произведения. 11. Условия коллинеарности и перпендикулярности векторов. Определение. Свойства. 12. Векторное произведение двух векторов. Определение. Свойства. 13. Координатная форма записи векторного произведения. 14. Смешанное произведение. Свойства. 15. Понятие двойного векторного произведения трех векторов.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.83.70 (0.009 с.) |

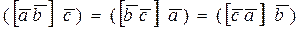

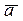

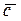 без знаков векторного и скалярного умножения.
без знаков векторного и скалярного умножения. ,
,  ,
, 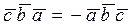 .
.


 (1.8.2.1)
(1.8.2.1)
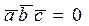 или
или 
 (1.9.1)
(1.9.1) (1.9.2)
(1.9.2)


