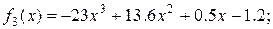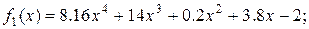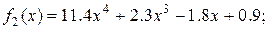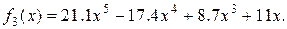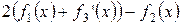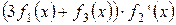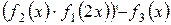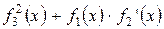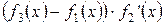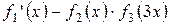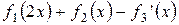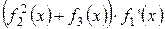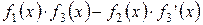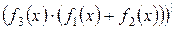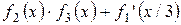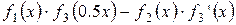Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вирахування значення ступiневого полiнома
Поліном (5.1) можна перетворити до вигляду:
Алгоритм вирахування
Якщо покласти У математицi доведено, що для поліномів загального вигляду не можна побудувати алгоритм бiльш ощадний у розумiннi числа операцiй (n додавань та n множень), анiж схема Горнера. У ML значення ступiневого полiнома з коефіцієнтами A вираховує функцiя Y = polyval (A, X), X – точки, у яких треба обчислити значення СП (може бути скалярною величиною або матрицею). Операцiї зi ступiневими полiномами Операцiї з СП складаються з двох частин: 1) формування нового СП, який є результатом операцiї, тобто розрахунок його коефiцiєнтiв; 2) вирахування значення нового СП. Нехай ми маємо два СП: Pn( A ,x) та Gm( B ,x). А результатом деякої операцiї є ще один СП Hk( C ,x). Для алгебраічного складання та віднімання поліномів Pn( A ,x) та Gm( B ,x) треба спочатку виконати вiдповiдну операцiю над масивами коефiцiєнтiв A та B. Але, зважаючи на те, що вони мають різний розмiр, попередньо треба доповнити менший за розмiром масив до бiльшого нулями злiва. Для цих операцiй розмір результата Hk( C ,x) можна знайти як k=max(m,n). Функцiя формування коефiцiєнтiв C ступiневого полiнома, який є алгебраічною сумою полiномiв з масивами коефiцiєнтiв A та B може мати вигляд: function C=polysum(A,B) n=length(A); m=length(B); if n>m, r=n-m; B=[zeros(1,r),B]; elseif m>n, r=m-n; A=[zeros(1,r),A]; end C=A+B; % end polysum Для виконання бiльш складних операцiй ML має встроєнi функцiї conv, deconv, polyder та інші. C = conv(A, B) – обчислює коефіцієнти ступіневого полінома, який є добутком двох поліномів з векторами коефіцієнтів А і В. Розмір вектора С визначається наступним чином: length(C)= length(A) + length(B) - 1. [D, R] = deconv(A, B) – операція розкладу, обчислює: D – коефіцієнти ступіневого полінома, отриманого від ділення полінома з вектором коефіцієнтів А на поліном з вектором коефіцієнтів В; R – остача від ділення. При цьому справедливе відношення: A = conv(D, B) + R. A1 = polyder(A) – обчислює коефіцієнти А1 ступіневого полінома, який є похідною полінома з коефіцієнтами А. [Q, D] = polyder(A, B) – обчислює чисельник Q і знаменник D похідної частки двох поліномів з векторами коефіцієнтів А і В, тобто
D = polyder(A, B) – обчислює коефіцієнти D похідної від добутка поліномів з векторами коефіцієнтів А і В, тобто D =(A • B)'.
Завдання Розрахувати значення змiнноi Z при x, який змiнюється вiд -1 до +1 з кроком 0.1. Вирази для вирахування Z наведенi у таблицi 5.1. В цих виразах функцiї f 1(x), f 2(x), f 3(x) є ступіневi поліноми, якi рiзняться один вiд одного порядком i значенням коефiцiєнтiв. Побудувати графіки функцій f 1(x), f 2(x), f 3(x)у одному вікні, Z (x) у другому вікні. Вивести на екран f 1(x), f 2(x), f 3(x)та Z (x) у вигляді СП. Для непарних варiантiв:
Для парних варiантiв:
Таблиця 5.1
Лабораторна робота № 6
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 112; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.101.95 (0.006 с.) |
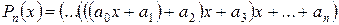 . (5.2)
. (5.2)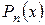 , складений на підставі виразу (5.2), називається схемою Горнера. У відповiдності до цієї схеми поліном i -го порядку обчислюється за формулою:
, складений на підставі виразу (5.2), називається схемою Горнера. У відповiдності до цієї схеми поліном i -го порядку обчислюється за формулою: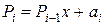 . (5.3)
. (5.3)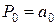 та виконати операцiю (5.3) n разiв при
та виконати операцiю (5.3) n разiв при 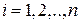 , то можна отримати бажане значення.
, то можна отримати бажане значення.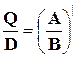 , або, якщо присутній один вихідний параметр:
, або, якщо присутній один вихідний параметр: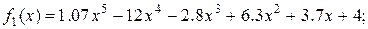
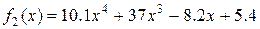 ;
;