
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функції будування графіків у декартових координатахСодержание книги
Поиск на нашем сайте
Найбільш розповсюдженою функцією для будування графіків у декартових координатах є функція plot. Формати визову: plot(y) – будує значення елементів вектора y в функції їх порядкового номеру (адреса) – yi = f(i); plot(x,y) – будує графік yi = f(xi); plot(z) – будує комплексні числа z (відповідає команді plot(real(zi),imag(zi))); plot(A) – будує рідню графіків, кожний з яких представляє собою залежність елементів одного стовпця матриці A в функції порядкового номеру рядка; plot(x, A) – теж саме, але в функції відповідного елемента вектора x. Довжина вектора x повинна бути рівною числу рядків матриці A. За замовчуванням графіки будуються відрізками безперервних ліній, які з’єднують між собою сусідні точки. Для придання плавності графіку треба брати не менше 50-100 точок. Колір кривій обирається автоматично, але при необхідності можна вручну вказати додаткові параметри (LineSpec) такі як колір, тип лінії або маркера (дивись help plot). В одній функції plot можна використовувати декілька груп аргументів. В цьому випадку всі графіки зображуються в одній системі координат в однаковому масштабі. При необхідності побудови графіків у логарифмічному масштабі по якій-небудь вісі треба використовувати функції: semilogx(x,y) – логарифмічний масштаб по осі x; semilogy(x,y) – логарифмічний масштаб по осі y; loglog(x,y) – логарифмічний масштаб по обох осях. Формат використання цих функцій такій же, як і у функції plot. За допомогою наступних функцій можна будувати графіки двох функцій з різним масштабом plotyy, завданої функції fplot. Формати визову: plotyy(x1, y1, x2, y2, fun1, fun2) – будує графіки функцій y1(x1) i y2(x2) в одному ГВ, fun1, fun2 (необов’язкові параметри) вказують тип графіка (‘ plot ’, ‘ semilogx ’, ‘ stem ’ і т.і.); fplot(fun, lims, 'LineSpec') – будує графік функції завданої виразом fun, lims – межі змінних [ xmin xmax ymin ymax ]. За допомогою наступних функцій можна будувати графіки у вигляді стовпців, сходинок, черенків, пирога: bar(y), bar(x,A), bar3(y) – побудування стовпчикових діаграм; stairs(x,y) – побудування східчастих графіків; stem(x,y) – побудування пікових (черенкових) діаграм; pie(y), pie(y, labels), pie(y, exsplode), pie3(y) – побудування кругових діаграм. Функції будування графіків у полярних координатах: polar(fi,ro) – будує графік в полярних координатах fi = f(ro), ro – в радіанах. Параметри лінії можна задавати в додатковому аргументі, варіанти значень якого такі ж самі, як і в функції plot;
compass(m,n) – зображує точку як вектор, направлений з начала координат; compass(z) – те ж саме, що і compass(real(z),imag(z)). Завдання
1-е ГВ: побудувати графік затухаючої синусоїди 2-е ГВ: Задати одномірний
4-e ГВ: Побудувати графік функції 5-е ГВ: Задати одномірний 6-е ГВ: Побудувати графіки у полярній системі координат (окружність, спіраль, еліпс). Рівняння еліпсу: Таблиця 4.1
Лабораторна робота № 5 ОПЕРАЦІЇ З ПОЛІНОМАМИ Цiль роботи: навчитися вираховувати значення ступiневих поліномів найбiльш ощадливим засобом та виконувати рiзноманiтнi операцiї з ними у середовищi пакета ML. Теоретичнi вiдомостi Загальнi поняття Ступiневим полiномом (СП) у математицi звуть функцiю, що має вигляд:
де n -ступінь полiному; A =[ a 0, a 1, …, an ] - вектор коефіцієнтів; x - незалежна змінна. СП широко використовуються у теорiї автоматичного керування в передатних та частотних функцiях.
В пакетi ML iнформацiя про СП зберiгається у виглядi матрицi-рядка коефiцiєнтiв, упорядкованих за зменшенням ступеню незалежної змiнної, тобто вектору A =[2 5 0 –8] вiдповiдає полiном Слiд мати на увазi, що нумерацiя елементiв масивiв у ML завжди починається з одиницi. Вивести СП на екран можна за допомогою функцiї P_str = poly2str (A, x_char) x_char – символьне зображення незалежної змiнної; P_str – СП у форматi строки символiв. Вивести на екран дві СП у виглядi дробi можна за допомогою функцiї P_str = printsys (B, A, x_char) де чисельник – поліном з коефіцієнтами В, а знаменник – поліном з коефіцієнтами А.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 162; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.92.89 (0.009 с.) |

 Скласти програму, яка демонструє можливості двовимірної графіки у ML, створивши 6 графічних вікон. Вихідні данні наведені у таблиці 4.1.
Скласти програму, яка демонструє можливості двовимірної графіки у ML, створивши 6 графічних вікон. Вихідні данні наведені у таблиці 4.1.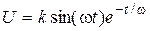 з огібаючими
з огібаючими  (різним кольором та різними типами ліній) на інтервалі 0¸9. Нанести сітку, пояснюючі надписи (заголовок, вісі, легенду).
(різним кольором та різними типами ліній) на інтервалі 0¸9. Нанести сітку, пояснюючі надписи (заголовок, вісі, легенду). і двомірний
і двомірний  масиви випадкових чисел. Відсортувати їх (
масиви випадкових чисел. Відсортувати їх ( і
і  ). Побудувати стовпчикові діаграми отриманих масивів у одному ГВ, розділивши його на 4 частини.
). Побудувати стовпчикові діаграми отриманих масивів у одному ГВ, розділивши його на 4 частини. 3-e ГВ: Побудувати графік функції
3-e ГВ: Побудувати графік функції  (парні варіанти) або
(парні варіанти) або  (непарні варіанти) на інтервалі 0¸3
(непарні варіанти) на інтервалі 0¸3  . В тому ж ГВ побудувати східчастий графік з шириною сходинки
. В тому ж ГВ побудувати східчастий графік з шириною сходинки  .
. масив випадкових чисел. Побудувати кругову діаграму.
масив випадкових чисел. Побудувати кругову діаграму.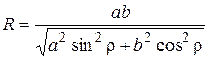 , спіралі
, спіралі 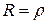 .
.


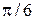


 , (5.1)
, (5.1) .
.


