
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы о математическом ожидании и дисперсии.
Доказательство проводится на примере дискретной случайной величины, для непрерывной случайной величины оно аналогично. Теорема 4.1. Математическое ожидание постоянной (неслучайной, т.е. детерминированной величины) равно этой постоянной. M[C]=C
Доказательство Постоянную С можно рассматривать как ДСВ, которая может принимать только одно значение С с вероятностью р =1, поэтому
Теорема 4.2. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий. Пусть X,Y – ДСВ или X,Y – НСВ. M[X+Y]=M[X]+M[Y]
Доказательство Рассмотрим случай, когда X и Y – ДСВ. Пусть x1, x2,…,xn,… - возможные значения СВ Х, и p1, p2,…,pn,… - их вероятности; y1, y2,…,yk,… - возможные значения СВ Y и q1, q2,…,qk,… - вероятности этих значений. Обозначим через pnk вероятность того, что СВ Х примет значение xn, а СВ Y – значение yk. Возможные значения величины X+Y имеют вид xn+yn (k,n=1,2,…)
Разделим эту сумму на составляющие:
Так как по теореме о полной вероятности
Теорема 4.3. Математическое ожидание произведения независимых случайных величин X и Y равно произведению их математических ожиданий.
Доказательство Если X и Y – дискретные случайные величины и x1, x2,…,xn,… - возможные значения СВ Х, p1, p2,…,pn,… - вероятности этих значений; y1, y2,…,yk,… - возможные значения СВ Y и q1, q2,…,qk,… - вероятности этих значений.
Следствие. Постоянный множитель можно выносить за знак математического ожидания:
Теорема 4.4. Математическое ожидание линейной функции случайной величины есть линейная функция математических ожиданий компонентов:
Доказательство.
D[C]=0.
Доказательство Или же
Теорема 4.6. Дисперсия суммы независимых случайных величин Х и Y равняется сумме дисперсий: D[X+Y]=D[X]+D[Y].
Дисперсией СВ Х называется математическое ожидание квадрата ее отклонения от ее математического ожидания:
т.к. СВ Х и Y независимы, то независимы и величины (Х-М[X]) и (Y-M[Y]), следовательно:
Следовательно, имеем
Следствие 1. Если Х1, Х2,…,Хn - случайные величины, каждая из которых независима от суммы предыдущих, то D[X1+X2+…+Xn]=D[X1]+D[X2]+…+D[Xn]
Следствие 2. Дисперсия сумма конечного числа попарно независимых случайных величин Х1, Х2,…, Хn равна сумме их дисперсий:
Теорема 6.7. Постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
Доказательство
Следствие.
Теорема 6.8. Если Х и Y независимы, то
Доказательство Основано на использовании соотношения
Dx= M[x2] – mx2 -> M[x2] = Dx + mx2
Имеем D[XY]= M[x2] M[Y2] - mx2mY2 = (Dx + mx2)(Dy + my2) - mx2mY2 =DxDy+Dxmy2+ Dymx2+ mx2 my2 - mx2 my2 = DxDy+Dxmy2+ Dymx2
Моменты. МО и дисперсия являются частным случаем моментов случайных величин. Различают начальные и центральные моменты. Начальным моментом k-ого порядка случайной величины X называют МО величины
Легко видеть, что характеристика положения - МО случайной величины – есть не что иное, как ее первый начальный момент, т.е.
Перед тем, как дать определение центральных моментов, введем новое понятие «центрированной случайной величины». Центрированной случайной величиной называют отклонение случайной величины от ее МО.
Нетрудно убедиться, что МО центрированной случайной величины равно 0.
Аналогично и для НСВ. Центрирование случайной величины равносильно переносу начала отсчета в точку Моменты интегрированной случайной величины называют центральными. Центральным моментом k-ого порядка случайной величины X называют МО k-ой степени центрирования случайной величины
Очевидно, что для любой случайной величины Х центральный момент 1-ого порядка равен нулю.
Второй центральный момент:
Между центральными и начальными моментами существует связь: одни выражаются через другие. Выведем соответствующие формулы для ДСВ (для НСВ аналогичен при замене Второй центральный момент:
Таким образом, дисперсию
т.е. дисперсия случайной величины равно МО ее квадрата минус квадрат математического ожидания. Найдем третий центральный момент:
пользуясь формулой для куба разности
т.к. Точно таким же способом можно получить выражения для Итак, центральные моменты выражаются через
МО, дисперсия – чаще всего применяемые числовые характеристики случайных величин. Они характеризуют, как видели ранее, самые важные черты распределения: его положение и степень разбросанности. Для более подробного описания распределения служат моменты высших порядков. Третий центральный момент Действительно, при симметричном распределении и нечетной k в сумме
каждому положительному слагаемому соответствует равное ему по абсолютной величине отрицательное слагаемое, так что они взаимно уничтожаются и сумма равна нулю (то же справедливо и относительно интеграла, выражающего Естественно поэтому в качестве характеристики асимметрии распределения выбрать какой-либо из нечетных моментов – проще всего
Для симметричной случайной величины S=0,
Четвертый центральный момент служит для характеристики так называемой «крутости», т.е. островершинности распределения (применяется в основном к НСВ). Это свойство характеризуется с помощью эксцесса:
Число 3 вычитается из отношения
Пример. Найти коэффициент симметрии и эксцесс случайной величины, распределенной по закону Лапласса с Решение.
Для нахождения эксцесса необходимо вычислить четные начальные моменты
Следовательно,
т.к.
Эксцесс:
3>0 Эксцесс положительный, следовательно, кривая распределения f(x) является островершинной.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1718; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.163.58 (0.073 с.) |


 ;
; .
. и
и  ,
,



 ,
,




 .
.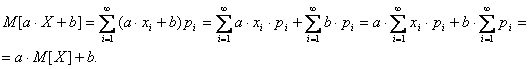

 , рассматриваем как ДСВ, которая принимает одно значение С с вероятностью 1.
, рассматриваем как ДСВ, которая принимает одно значение С с вероятностью 1. .
.


 .
.
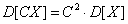 , где С=const.
, где С=const.
 .
.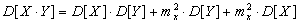 .
.
 D[XY]=M[ (XY- M[XY])2] = M[ (XY - mxmy)2] = M[X2Y2]- 2M[XYmxmy]+M[mx2my2] = M[x2]M[Y2] – 2mxmY mxmY+ mx2mY2 = M[x2]M[Y2] - mx2mY2
D[XY]=M[ (XY- M[XY])2] = M[ (XY - mxmy)2] = M[X2Y2]- 2M[XYmxmy]+M[mx2my2] = M[x2]M[Y2] – 2mxmY mxmY+ mx2mY2 = M[x2]M[Y2] - mx2mY2
 и
и  .
. (т.е. МО k-ой степени это величины):
(т.е. МО k-ой степени это величины):


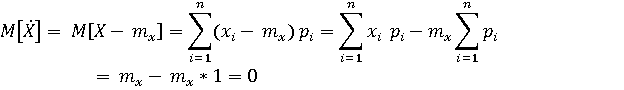
 (центр распределения).
(центр распределения).

 ;
; 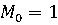 , т.к.
, т.к.  =
= 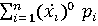 =1
=1
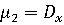
 на
на  на f(x)) dx, сумм на интегралы).
на f(x)) dx, сумм на интегралы). =
= 
 , т.к.
, т.к. 

 можно рассчитывать как
можно рассчитывать как



 =
=  ,
,
 и т.д.
и т.д. начальные формулы:
начальные формулы: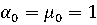


 и т.д.
и т.д. служит для характеристики асимметрии («скошенности») распределения. Если распределение симметрично относительно МО, то все центральные моменты нечетного порядка (если они существуют) равны нулю.
служит для характеристики асимметрии («скошенности») распределения. Если распределение симметрично относительно МО, то все центральные моменты нечетного порядка (если они существуют) равны нулю.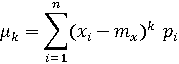
 для нечетного k, который равен нулю как интеграл в симметричных пределах от нечетной функции).
для нечетного k, который равен нулю как интеграл в симметричных пределах от нечетной функции). или
или 




 потому что для часто встречающегося нормального распределения
потому что для часто встречающегося нормального распределения  . Для нормального распределения
. Для нормального распределения 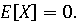 Кривые, более островершинные, чем нормальная, обладают положительным эксцессом, а более плосковершинные – отрицательным. Характеристикой
Кривые, более островершинные, чем нормальная, обладают положительным эксцессом, а более плосковершинные – отрицательным. Характеристикой 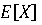 пользуются главным образом для симметричных распределений.
пользуются главным образом для симметричных распределений.
 .
. Т.к. распределение случайной величины симметрично относительно оси ординат, то все нечетные как начальные, так и центральные моменты равны нулю, т.е.
Т.к. распределение случайной величины симметрично относительно оси ординат, то все нечетные как начальные, так и центральные моменты равны нулю, т.е. 
 и, следовательно, коэффициент симметрии
и, следовательно, коэффициент симметрии 
 2* ½
2* ½ 

 =
= 

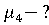

 , то
, то 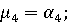
 2* ½
2* ½ 




