
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое ожидание и дисперсия классических распределений.
Найдем значения математического ожидания и дисперсии для некоторых законов распределения. Биномиальное распределение. Известно, что биномиальное распределение описывается формулой: а математическое ожидание для дискретных случайных величин рассчитывается по формуле: Тогда имеем Следовательно, M[x]=np – с точностью до целого совпадает с модой (наивероятнейшим значением). Аналогично можно рассчитать дисперсию: Dx=npq.
Распределение Пуассона. (m=0,1,2,….). Найдем математическое ожидание. = ae-a
Таким образом, Найдем дисперсию. Для дискретных случайных величин: (m-a)2=m2 - 2ma + a2 = (m2 – m) – (2ma - m) +a 2 = m(m – 1) – m (2a + 1) +a2 Тогда получаем: Dx = = =
Таким образом, для закона Пуассона M[X]= D[X]= a = параметру закона.
Распределение равномерной плотности
Замечание. Учитывая, что при
Нормальное распределение
Найдем дисперсию нормального закона распределения.
Величина mx СВ Х, подчиненной нормальному закону распределения, называется ее центром рассеивания. Размерности как МО так и С.К.О. совпадают с размерностью СВ Х. Посмотрим, как будет меняться кривая распределения при изменении параметров При изменении а кривая f(x), не изменяя своей формы просто будет смещаться вдоль оси абсцисс. Изменение s равносильно изменению масштаба кривой по обеим осям: например, при удвоении s масштаб по оси абсцисс удвоится, а по оси ординат – уменьшится в 2 раза.
Рисунок 6.4
Оценим для нормальной СВ Х вероятность попадания на участок от a до b, где a= а-кs и b= а+ks, т.е вероятность попадания в интервал а±ks симметричный относительно mx=a. Выше были получены формулы: В данном случае Пусть k=1, тогда: k=2, k=3, т.е. всего с вероятностью 0,0027 случайная величина, распределенная по нормальному закону, попадает за пределы интервала
Рисунок 6.5
С большой точностью Х попадет внутрь этого интервала. Это правило называется правилом «трех σ» для нахождения интервала рассеивания. Зная этот интервал возможного рассеивания случайной величины Х ( Для неотрицательной СВ Х в качестве характеристики ее «случайности» иногда применяется коэффициент вариации
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.168.16 (0.012 с.) |
 ,
, .
.
 ,
,
 =a
=a M[x]=a
M[x]=a
 ,
, .
. =
= =
=
 =
=
 .
. .
.
 ,
, .
. 3. 4. Показательное распределение
3. 4. Показательное распределение .
. .
.
 быстрее, чем возрастает степень х.
быстрее, чем возрастает степень х.

 .
.


 .
. .
. равна
равна  , а
, а  . Значит, параметр
. Значит, параметр  есть не что иное как С.К.О СВ Х.
есть не что иное как С.К.О СВ Х.
 .
.
 - вероятность попадания нормально распределенной СВ Х на интервал от a до b;
- вероятность попадания нормально распределенной СВ Х на интервал от a до b; или
или 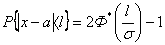 - это вероятность попадания СВ Х на участок длиной 2 l, симметричный относительно центра рассеивания а.
- это вероятность попадания СВ Х на участок длиной 2 l, симметричный относительно центра рассеивания а. .
. ;
; ;
; ,
, .
.
 ) вокруг mx=a, можно найти
) вокруг mx=a, можно найти  .
. .
.


