Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моменты двумерного случайного вектора. Коэффициент корреляции
При наличии двух случайных величин X и Y важно знать влияние одной на другую. Например, X-объем памяти, занимаемый программой из пакета прикладных программ, Y-время счёта по программе. Каждой конкретной программе из пакета соответствует точка на плоскости (x,y).
Существует определённая зависимость Наиболее часто рассматривают только линейную регрессию
где коэффициенты a и b выбираются так, чтобы получить наибольшую концентрацию точек (х,у) вблизи прямой регрессии
Определение 7.1. Начальным моментом порядка k+s случайного вектора (X,Y) называют математическое ожидание произведения
В частности:
Точка с координатами
Определение 7.2 Центральным моментом порядка k+s называют математическое ожидание произведения
или
В частности Второй смешанный центральный момент или cov(X,Y)=
Физический смысл
Теорема 7.1. Если X и Y независимые случайные величины, то их корреляционный момент равен нулю. Доказательство. Так как X и Y независимы, то f(x,y)=f(x)f(y) и
т.е. независимые случайные величины некоррелированы (несвязаны). Обратное верно не всегда. Условие некоррелированности – необходимое, но не достаточное условие их независимости, т.к. Корреляционный момент
При
Приведём без доказательства, что
Коэффициент корреляции Значение корреляционного момента
Теорема 7.2 Математическое ожидание произведения двух случайных величин равно произведению их МО плюс их корреляционный момент.
Доказательство.
Теорема 7.2 Дисперсия суммы случайных величин равна сумме их дисперсии и удвоенного корреляционного момента:
Доказательство. D[XY]=M[((x+y) –M[x+y])2] = M[((X-
Следствие
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.142.128 (0.006 с.) |

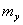 от X
от X 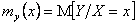 , которая называется регрессией Y по X.
, которая называется регрессией Y по X. (x)=ax+b,
(x)=ax+b, , т.е.
, т.е.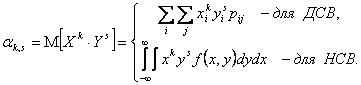
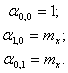

 - центр распределения (рассеивания)
- центр распределения (рассеивания)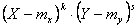 , т.е.
, т.е.

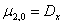 ,
, 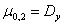 .
.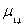 ввиду своей важности получил специальное название: коэффициент ковариации (или корреляционный момент) и обозначение
ввиду своей важности получил специальное название: коэффициент ковариации (или корреляционный момент) и обозначение 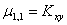
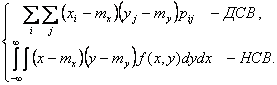
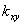 - степень зависимости между X и Y.
- степень зависимости между X и Y. ,
,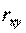 ,
, 
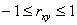 .
.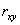 =0, X и Y некоррелированы.
=0, X и Y некоррелированы.


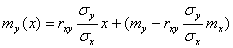 или
или  .
. характеризует не всякую, а только линейную зависимость случайных величин X и Y, т.е. при наличии некоторых нелинейных зависимостей он может равняться нулю.
характеризует не всякую, а только линейную зависимость случайных величин X и Y, т.е. при наличии некоторых нелинейных зависимостей он может равняться нулю.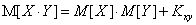 .
.
 .
.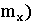 +(Y-
+(Y- 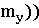 2] =
2] =