
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эффективная площадь рассеяния облаковСодержание книги
Поиск на нашем сайте
При радиолокационных наблюдениях облаков и осадков, наблюдается множественная цель, характеризующая суммарную мощность отраженных сигналов от отдельных гидрометеоров. Для оценки суммарной мощности рассеяния сигнала вводят понятие удельной эффективной площади рассеяния
Если имеем монодисперсное облако, то:
Расчет интенсивности рассеянной энергии объемом, который содержит частицы облаков и осадков требует знания аналитических выражения для функции распределения капель по размерам. Необходимы знания спектра частиц. Спектр – это самостоятельная характеристика облака, однозначно связанная с водностью облака и интенсивностью осадков. На спектр облачных капель оказывают влияние процессы конденсации, коагуляции и испарения. Коагуляция и гравитация играют роль для гидрометеоров или облачных частиц, радиус которых больше или равен 15 мкм. Из-за сложности процессов в облаке рассмотрим определенные спектры по большому числу измерений на разных стадиях развития. Для облаков слоистых форм спектр облачных частиц описывается формулой Хргиана-Мазина:
где Пример: Для крупных части
В этом выражении: Пример: St Если имеем выпадающие осадки, то среднее распределение капель дождя по размерам может быть представлено:
где Пример:
Если имеем радиолокационную станцию с шириной диаграммы
Рассеянный, отраженный сигнал будет возвращаться из пространства
Предположим, что вырезанный в пространстве объем будет определяться цилиндром, и мы можем определить площадь основания такого цилиндра s New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>2</m:t></m:r></m:den></m:f><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> Если возьмем по всему расстоянию Вводится понятие разрешающий объем, который будет определяться:
Предположим, что в разрешающим объеме находится
где
Для случая неоднородных полидисперсных частиц в разрешающем объеме ЭПР будет определяться:
(*) и (**) справедливы, если весь зондирующий объем заполнен облаками, если объем не полный, то вводиться коэффициент заполнения:
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.168.219 (0.009 с.) |

 , т.е. эффективная площадь рассеянных частиц в единице объема (см3, м3).
, т.е. эффективная площадь рассеянных частиц в единице объема (см3, м3).
 (1) – для всех частиц, где
(1) – для всех частиц, где  – эффективная площадь рассеяния отдельной частицы,
– эффективная площадь рассеяния отдельной частицы,  - число капель в единице объема.
- число капель в единице объема. (2) – только для монодисперсной облачности.
(2) – только для монодисперсной облачности.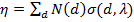 – для полидисперсной облачности, где
– для полидисперсной облачности, где 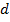 - диаметр гидрометеоров,
- диаметр гидрометеоров,  – функция распределения гидрометеоров по размерам.
– функция распределения гидрометеоров по размерам. ,
,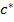 - постоянная, зависящая от формы облаков;
- постоянная, зависящая от формы облаков;  – число капель, заключенных в интервале
– число капель, заключенных в интервале  ,
,  .
. , где
, где  - плотность вещества капли,
- плотность вещества капли, 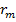 – максимальный радиус капли.
– максимальный радиус капли.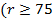 мкм) спектр облачных частиц будет описываться:
мкм) спектр облачных частиц будет описываться:
 - число частиц, превышающих определенный порог;
- число частиц, превышающих определенный порог;  – минимальный размер капель, которые регистрируются прибором,
– минимальный размер капель, которые регистрируются прибором, 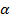 - показатель спада кривой распределения для различных облаков.
- показатель спада кривой распределения для различных облаков. Sc
Sc  ; Ns
; Ns  .
. ,
, - размер дождевых капель,
- размер дождевых капель,  – множитель, который зависит от интенсивности выпадающих осадков.
– множитель, который зависит от интенсивности выпадающих осадков. и длительностью посылаемых импульсов
и длительностью посылаемых импульсов  , то такой посылаемый импульс будет занимать объем
, то такой посылаемый импульс будет занимать объем  (
( – скорость распределения электромагнитных волн).
– скорость распределения электромагнитных волн). .
.
 .
. , то
, то  – по всей сфере на расстоянии
– по всей сфере на расстоянии 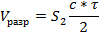

 монодисперсных сферических частиц. Тогда:
монодисперсных сферических частиц. Тогда:
 ,
, – ЭПР разрешающего объема.
– ЭПР разрешающего объема.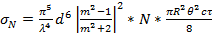 (*)
(*) (**)
(**) .
.


