
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимодействие электромагнитных волн с окружающей средой (атмосферой)Стр 1 из 14Следующая ⇒
Лекция №1 Лекция №2
При анализе решения уравнения (10) имеет место следующее: по мере распространения волны ее составляющие Составляющие
Амплитуды электромагнитных волн составляющих связаны между собой:
Лекция №3 2) Атмосфера с наличием гидрометеоров и облаков – ледяные (или водяные) частички облаков и выпадающие осадки в атмосфере относятся к полупроводящей среде с потерями. Для таких сред определяется диэлектрическая проницаемость:
Для воды: Как видно из соотношений (18) и (19), как действительная, так и мнимая части комплексной диэлектрической проницаемости зависят от длины падающей волны. Для длин волн
Атмосферное образование - это влажный воздух и взвешенные гидрометеорные частицы. Тогда:
Если облачные образования состоят из сферических частиц, равномерно распределенных в пространстве, то электрическая восприимчивость облачных частиц определяется следующим выражением:
Первое и второе слагаемые в выражении (24) определяют вклад в величину показателя преломления влажного воздуха, третье слагаемое – это вклад показателя преломления облачных образований.
Радиорефракция в атмосфере Радиоволны СМ-диапазона в атмосфере распространяются непрямолинейно, а криволинейной траектории. Это связано как с изменением показателя преломления с высотой, так и диэлектрической проницаемостью (P, T, e). Убывание этих параметров с высотой приводит к убыванию
Электромагнитный луч переходит из более плотной среды n1 в менее плотную среду n2, при этом траектория луча обращена вогнутостью в сторону границы раздела сред. Если электромагнитная волна распространяется над поверхностью Земли:
Рассмотрим
Подставим (2) в (1): Если электромагнитная волна распространяется в плоскослоистой атмосфере, где коэффициент преломления уменьшается, будет происходить плавное искривление радиолуча. Радиус кривизны траектории луча будет определяться градиентом коэффициента преломления. Когда радиус кривизны радиолуча направлен вдоль земной поверхности, тогда этот радиус будет равен радиусу кривизны самой поверхности земной поверхности. При этом луч огибает земной шар. При этих условиях наблюдается так называемая критическая рефракция электромагнитных волн. Если мы знаем значение градиента преломления, то мы можем определить значение критической рефракции:
В зависимости от характера искривления радиолуча различают три вида (основных) рефракции: 1) отрицательная; 2) нулевая; 3) положительная.
При сверхрефракции радиус кривизны радиолуча меньше радиуса земного шара, вследствие чего луч испытывает многократное отражение от земной поверхности, что приводит к сверхдальнему распространению радиоволны в атмосфере. Условия сверхрефракции: 1) при перемещении теплых сухих масс воздуха с континента на более холодную морскую поверхность приводит к уменьшению парциального давления водяного пара с высотой, при этом температура воздуха с высотой растет; 2) волноводное (критическое) распространение радиоволн может наблюдаться при перемещении холодного воздуха над теплым, при этом наблюдается резкое уменьшение парциального давления водяного пара с высотой, а градиент 3) над сушей при ясной безоблачной погоде ночью при возникновении приземных радиационных инверсий температур, сопровождаемых образование росы, возникает сверхкритическая рефракция, т.к. утром с восходом Солнца происходит резкое уменьшение влажности с высотой;
4) в области повышенного давление вследствие оседания воздуха образуется инверсия сжатия, в этих случаях наблюдаются приподнятые атмосферные волноводы, иногда они сливаются, образуя высокие волноводы (воздушный слой, где происходит распределение волны по горизонтали). Явление сверхрефракции зависит от синоптической обстановки, что позволяет прогнозировать ее проявление по метеорологическим данным.
Лекция №4 Методы учета радиорефракции Искривление траектории радиолуча при распространении в атмосфере приводит к ошибкам при измерении высоты объектов над поверхностью Земли. Различают два метода: 1) метод эквивалентного радиуса Земли; 2) метод приведенного коэффициента преломления. Первый метод сводится к решению задачи криволинейного распределения радиоволн в условиях реальной атмосферы. Криволинейную траекторию при этом «разгибают» до тех пор, пока траектория луча не будет прямолинейной. Полученный радиус сферы, над которой распределяется радиолуч, – это эквивалентный радиус ( Для определения Если возьмем две точки, одна из которых расположена на поверхности Земли, а вторая на высоте
где
Уравнение (1) при условии (2):
Из (3):
Сравним (1) и (5), представим, что Условия для реальной атмосферы:
В (6):
Вычисленный
Если нулевая рефракция, то Учет влияния радиорефракции сводится к замене Приведение радиуса кривизны Земли к эквивалентному, уменьшает искривления радиолуча, т.е. мы выпрямляем радиолуч относительно новой сферы
Используя параметр эквивалентного радиуса можно определить дальность распространения радиоволн и определить дальность радиогоризонта, который позволяет определить дальность радиолокационного обнаружения объекта
где H – высота объекта, H0 – высота антенны над поверхностью Земли.
В (9) подставляем
Для определения высоты объекта используется:
где
Второй метод – метод приведенного коэффициента преломления, который заключается в том, что влияние земной кривизны и кривизны сферической слоистой атмосферы заменяют влиянием дополнительного значения коэффициента преломления атмосферы. Для этого криволинейную траекторию луча с земной поверхностью «разгибают» до тех пор, пока сферическая поверхность Земли не превратиться в плоскую и радиолуч при этом будет иметь другую кривизну, близкую к прямолинейной. Соответствуя новой рефракции, коэффициент преломления называют приведенным коэффициентом преломления. Если из точки, расположенной на земной поверхности, в плоскослоистую атмосферу направлен радиолуч, то справедливо:
т.к.
Приведенный коэффициент преломления используется в задачах радиорефракции при распространении радиоволн над плоской поверхностью Земли.
Лекция №5
Для расчетов коэффициента поглощения водяным паром вне области резонанса используется следующая зависимость:
где Учитывая уменьшение давления и температуры с высотой можно записать, что:
где Если мы рассмотри интервал поглощения радиоволн в водяном паре, то:
где Таким образом, коэффициент поглощения электромагнитной энергии атмосферой вне области резонанса в зависимости от высоты можно определить выражением:
Потери электромагнитной энергии в газах учитываются удельным коэффициентом поглощения (удельный коэффициент, т.е. на единицу расстояния), который является суммарным где r – протяженность трассы, где распространяется электромагнитная волна, т.е. данное выражение дает суммарный коэффициент ослабления для слоя, протяженностью r. Принимаемая мощность электромагнитного излучения с учетом ослабления на трассе будет определяться следующим выражением:
где Применительно к радиолокации, когда сигнал радиоизлучения проходит двойное расстояние:
Как у кислорода, так и у водяного пара наблюдаются области частот, где поглощение велико. Для кислорода при
Для водяного пара при На длине волны около 3 см (МРЛ-2, МРЛ-5) удельный коэффициент ослабления в кислороде будет определяться следующим выражением II. Ослабление радиоволн гидрометеорами облаков без осадков. Электромагнитные волны, взаимодействуя с гидрометеорами в облаке, испытывают поглощение и рассеяние, при этом соотношение между диаметром частицы d и длиной волны
где Если электромагнитная волна проходит элементарный участок Для оценки поглощения и рассеяния на участке
с учетом
Если мы проинтегрируем (2) по расстоянию от 0 до R, а по мощности от
Выражение (3) преобразим, перейдя от натурального логарифма к десятичному:
Полное ослабление гидрометеорами включает сумму удельных коэффициентов поглощения и рассеяния:
Если выполняется
где
где Для малых частиц, когда Для больших частиц Для крупных частиц водность облака определяется следующим выражением:
где N – количество частиц,
Для жидких гидрометеоров:
Если Можем оценить, что коэффициент ослабления суммарный (для водного облака):
Для ледяного облака:
где q - это удельная влажность. Если облако без осадков, то суммарный коэффициент ослабления
Лекция №6 Лекция №7 Как будет меняться эффективная площадь рассеянных частиц, которые будут состоять из водяной и ледяной консистенции. Зависимость эффективной площади рассеяния для МРЛ, работающих на Используя формулы Ми, было рассчитана площадь эффективного рассеяния:
Как видно из рисунков 1 и 2, наблюдается зависимость ЭПР от длины волны. С ростом диаметров гидрометеоров растет ЭПР, следовательно, фазовые состояния также оказывают влияние на ЭПР. Увеличение размеров гидрометеоров приводят к росту ЭПР. Если возьмем предельные значения гидрометеоров, то эффективная площадь рассеяния будет приближаться к предельному значению пропорционально
Лекция №8 Кроме отражаемости вводится эквивалентная отражаемость. Эквивалентная отражаемость характеризует свойства единичного объема облака или осадков или равна отражаемости капельного облака, который формирует равный по амплитуде отраженный сигнал:
Если облако кристаллическое и состоит из ледяных кристаллов, то:
Для крупных частиц эквивалентная отражаемость будет отражаться следующей эмпирической формулой:
где Отражаемость жидких осадков Рассеянный и отраженный сигнал зависит от размера гидрометеоров, количество которых определяется интенсивностью дождя. Радиус мороси от 0,025 мкм до 0,25 мкм и наиболее крупных капель 3-4 мм. Среднее распределение капель дождя по размерам описывается следующим выражением:
где Если Мелкие капли осадков имеют сферическую форму, однако крупные капли дождя приобретают форму сплющенных эллипсоид. Спектр капель дождя изменяется во времени и пространстве и зависит от типа облачности, из которой выпадают эти осадки. Интенсивность осадков определяется:
где В результате микрофизических исследований распределения частиц осадков по размерам Маршалом и Пальмером была получена зависимость между
где Данное выражение дает наиболее точную оценку интенсивности осадков Связь между
Для удельной ЭПР
Лекция №9
Введем постоянную радиолокатора
С учетом шумов приемника уравнение примет (13) примет вид:
Уравнение (14) – основное уравнение радиолокации метеорологических объектов, где мощность информационного рассеивающего сигнала оценивается по отношению к уровню собственных шумов приемника (
Отражаемость:
Если использовать выражение, характеризующее свойства рассеивания объекта через
Обозначим
Уравнение (18) запишем в виде:
С учетом уравнения (16):
Так, как постоянная радиолокации
Если нам перейти от диаметра антенны к геометрической площади
Величина
Для практических расчетов уравнение радиолокации можно представить в виде уравнения (20). Максимальная дальность обнаружения метеообъектов определяется следующим выражением:
Из выражения (22): отмечается зависимость максимального обнаружения от отражающих свойств объекта и чувствительности приемника РЛС. При выводе основного уравнения радиолокации сделаны следующие упрощения: 1) Рассматривалось распространение плоской электромагнитной волны в свободном пространстве без учета рефракции. При учете реальных условий распространения электромагнитной волны необходимо ввести некоторый множитель 2) При выводе основного уравнения радиолокации не учитывается ослабление электромагнитных волн на пути распространения. Для учета ослабления необходимо в правой части уравнения ввести коэффициент 3) Предполагалось, что весь импульсный объем метеообъекта занят рассеивающими частицами. В реальных условиях необходимо вводить коэффициент заполнения 4) Считалось, что рассеивание электромагнитных волн некогерентное, однократное. В действительности наблюдается интерференция электромагнитных полей от отдельных элементов рассеивателей, что приводит к существенному изменению величины принимаемого сигнала. Этот эффект можно учесть введением поправочного коэффициента в правой части уравнения радиолокации. С учетом возможных предположений основного уравнения радиолокации:
где Таким образом, уравнения (23) и (24) позволяют по величине измеренного отраженного сигнала определить отражаемость метеорологических объектов, находящихся на определенном расстоянии от РЛС.
Ввиду сложного распределения отражаемости в вертикальном и горизонтальном направлении, можно получить дополнительные характеристики в виде вертикального и горизонтального профиля отражаемости, т.е. можно получить пространственные и временные градиенты отражаемости.
Двухволновой метод для определения града Метод базируется на различие частотной зависимости рассеивания радиоволн гидрометеорами разных размеров. Он создан в результате теоретических исследований рассеивания радиоволн СМ-диапазона. Моделирование спектра гидрометеоров (капли, град, крупа, снег) и экспериментальные многоволновые радиолокационные исследования конвективных облаков позволили уточнить ряд положений. Принцип двухволнового метода основан на радиолокационных измерениях размеров гидрометеоров и разделения облачных объемов на градовые и не градовые облака по их микроструктуре.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 590; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.242.165 (0.182 с.) |
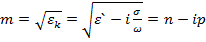 , где n - вещественная часть комплексного коэффициента преломления, называется показателем преломления, а мнимая часть p – показатель поглощения электромагнитной волны. Анализ зависимости комплексного коэффициента преломления от частоты ω показывает, что
, где n - вещественная часть комплексного коэффициента преломления, называется показателем преломления, а мнимая часть p – показатель поглощения электромагнитной волны. Анализ зависимости комплексного коэффициента преломления от частоты ω показывает, что  , когда
, когда  - электромагнитная волна в среде в основном преломляется,
- электромагнитная волна в среде в основном преломляется,  .
. ;
;
 испытывают ослабление, которое определяется множителем
испытывают ослабление, которое определяется множителем  .
. :
:
 , где
, где  - волновое сопротивление среды.
- волновое сопротивление среды.
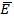 и магнитного поля
и магнитного поля  убывают обратно пропорционально расстоянию. Плотность потока мощности
убывают обратно пропорционально расстоянию. Плотность потока мощности  изменяется обратное пропорционально квадрату расстояния.
изменяется обратное пропорционально квадрату расстояния. (17), где
(17), где  - действительная и мнимая части комплексной диэлектрической проницаемости. Согласно теории Дебая:
- действительная и мнимая части комплексной диэлектрической проницаемости. Согласно теории Дебая: (18);
(18); (19), где
(19), где  – это оптический коэффициент преломления гидрометеоров,
– это оптический коэффициент преломления гидрометеоров,  - статически постоянная диэлектрическая проницаемость,
- статически постоянная диэлектрическая проницаемость,  – длина волны, которая соответствует максимальному значению действительной части диэлектрической проницаемости,
– длина волны, которая соответствует максимальному значению действительной части диэлектрической проницаемости,  - длина волны излучения, которая облучает гидрометеор.
- длина волны излучения, которая облучает гидрометеор. см.
см. см комплексная диэлектрическая проницаемость является действительной величиной. При увеличении
см комплексная диэлектрическая проницаемость является действительной величиной. При увеличении  см, действительная и мнимая части оказываются примерно равными. При
см, действительная и мнимая части оказываются примерно равными. При  см – мнимая часть превышает действительную часть диэлектрической проницаемости.
см – мнимая часть превышает действительную часть диэлектрической проницаемости. (20) – электрические восприимчивости;
(20) – электрические восприимчивости; (21), где
(21), где  - атмосферы, облачных образований.
- атмосферы, облачных образований. - число частиц в единице объема, a – средний радиус частицы, m – комплексный показатель преломления (
- число частиц в единице объема, a – средний радиус частицы, m – комплексный показатель преломления ( ).
). , где
, где  - плотность частицы,
- плотность частицы,  - водность частицы.
- водность частицы. (22)
(22) (23)
(23) (24)
(24) г/м3,
г/м3, 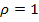 , а
, а  , в этом случае величина третьего слагаемого почти на 3 порядка меньше, чем величина второго слагаемого. Можем сделать вывод, что коэффициент преломления в атмосфере в основном определяется давлением, температурой и упругостью водяного пара, а гидрометеорные и облачные частицы не оказывают существенного влияния на величину показателя преломления. Однако, в Cb второе и третье слагаемые могут быть сопоставимы и величина показателя преломления в таких атмосферных образованиях может отличаться от показателя преломления безоблачной атмосферы.
, в этом случае величина третьего слагаемого почти на 3 порядка меньше, чем величина второго слагаемого. Можем сделать вывод, что коэффициент преломления в атмосфере в основном определяется давлением, температурой и упругостью водяного пара, а гидрометеорные и облачные частицы не оказывают существенного влияния на величину показателя преломления. Однако, в Cb второе и третье слагаемые могут быть сопоставимы и величина показателя преломления в таких атмосферных образованиях может отличаться от показателя преломления безоблачной атмосферы. и
и  . Показатель преломления определяется как отношение скорости распределения радиоволн в вакууме к скорости распределения радиоволн в реальной атмосфере. Так как показатель преломления в верхней части атмосферы меньше, чем в нижних слоях, скорость распространения радиоволн увеличивается с высотой, поэтому траектория луча изгибается вниз к Земле. В оптическом диапазоне электромагнитные волны распределяются по прямолинейной траектории, и в этом диапазоне вводится понятие оптического горизонта. При переходе в радиодиапазон вводится понятие радиогоризонта. Радиогоризонт больше оптического горизонта, так как водяной пар оказывает больше влияния на распределение электромагнитных волн в радиодиапазоне, чем в оптическом. Дальность радиогоризонта в среднем на 15% больше, чем дальность оптического горизонта. Радиорефракция в атмосфере и рассеяние до радиогоризонта определяется не абсолютными значениями
. Показатель преломления определяется как отношение скорости распределения радиоволн в вакууме к скорости распределения радиоволн в реальной атмосфере. Так как показатель преломления в верхней части атмосферы меньше, чем в нижних слоях, скорость распространения радиоволн увеличивается с высотой, поэтому траектория луча изгибается вниз к Земле. В оптическом диапазоне электромагнитные волны распределяются по прямолинейной траектории, и в этом диапазоне вводится понятие оптического горизонта. При переходе в радиодиапазон вводится понятие радиогоризонта. Радиогоризонт больше оптического горизонта, так как водяной пар оказывает больше влияния на распределение электромагнитных волн в радиодиапазоне, чем в оптическом. Дальность радиогоризонта в среднем на 15% больше, чем дальность оптического горизонта. Радиорефракция в атмосфере и рассеяние до радиогоризонта определяется не абсолютными значениями  .
.

 (1).
(1). (по теореме синусов):
(по теореме синусов): , где
, где  и
и 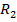 - расстояние от A и B до центра Земли.
- расстояние от A и B до центра Земли. .
. м-1.
м-1. , м-1
, м-1







 ).
). и первоначально луч распределяется под углом
и первоначально луч распределяется под углом 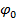 относительно вертикали.
относительно вертикали. , то на основании соотношения
, то на основании соотношения  :
: (1),
(1), (2)
(2) (3)
(3) (4)
(4)
 (5)
(5) , в этих условиях
, в этих условиях  , следовательно, радиорефракция отсутствует и радиус кривизны
, следовательно, радиорефракция отсутствует и радиус кривизны  .
. . Тогда:
. Тогда: (6) – эквивалентный радиус
(6) – эквивалентный радиус (7)
(7) (8)
(8)
 .
. на эквивалентный
на эквивалентный 
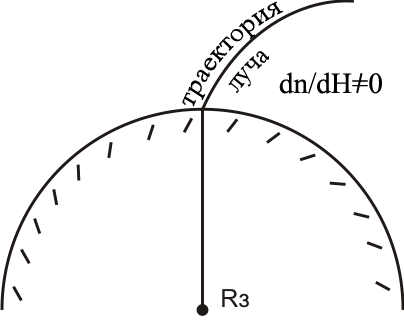
 .
. (9),
(9), .
.
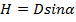 , где D – наклонная дальность, α – вертикальный угол.
, где D – наклонная дальность, α – вертикальный угол. ,
, - коэффициент рефракции,
- коэффициент рефракции,  – учитывает направление траектории луча в условиях нормальной атмосферной рефракции (стандартная атмосфера).
– учитывает направление траектории луча в условиях нормальной атмосферной рефракции (стандартная атмосфера).
 (1),
(1), , то (1):
, то (1):  (2), при этом
(2), при этом  (3).
(3).
 – эквивалентная длина поглощения. В случае экспоненциальной высотной зависимости
– эквивалентная длина поглощения. В случае экспоненциальной высотной зависимости  ЭДП совпадает с эффективной высотой кислорода и равна 5,3 км.
ЭДП совпадает с эффективной высотой кислорода и равна 5,3 км. (8),
(8), - абсолютная влажность воздуха, p – давление.
- абсолютная влажность воздуха, p – давление. (9),
(9), – величина, которая называется эффективной высотой слоя водяного пара, а
– величина, которая называется эффективной высотой слоя водяного пара, а  - коэффициент поглощения водяным паром на Земле.
- коэффициент поглощения водяным паром на Земле. или
или  (10),
(10), - эквивалентная длина поглощения водяного пара.
- эквивалентная длина поглощения водяного пара. (11)
(11) ,
, ,
, - начальная излучаемая мощность источника.
- начальная излучаемая мощность источника. .
. – множитель ослабления, который учитывает ослабления электромагнитной энергии в газах.
– множитель ослабления, который учитывает ослабления электромагнитной энергии в газах.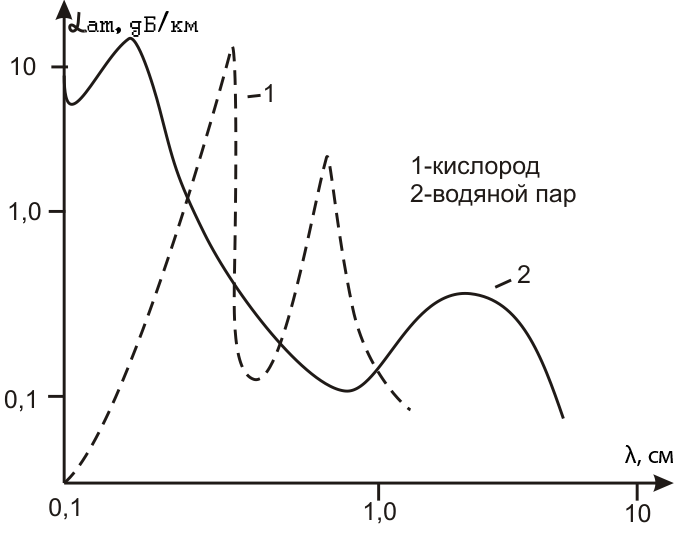
 наблюдается ослабление 3 дб/км, а для
наблюдается ослабление 3 дб/км, а для  – 14 дб/км.
– 14 дб/км. - 20 дб/км,
- 20 дб/км,  - 0,2 дб/км.
- 0,2 дб/км. дб/км, а для водяного пара
дб/км, а для водяного пара  дб/км. При водности 7,5 г/м3 коэффициент ослабления
дб/км. При водности 7,5 г/м3 коэффициент ослабления  дб/км.
дб/км. – волновое число. Интенсивность поглощения гидрометеорами оценивается с помощью эффективной площади поглощения (ЭПП)
– волновое число. Интенсивность поглощения гидрометеорами оценивается с помощью эффективной площади поглощения (ЭПП)  – отдельной частицы), и кроме того интенсивность рассеяния оценивается с помощью эффективной площади рассеяния (ЭПР)
– отдельной частицы), и кроме того интенсивность рассеяния оценивается с помощью эффективной площади рассеяния (ЭПР)  .
. ,
, ,
,  – мощности, теряемые падающей электромагнитной волной в результате поглощения и рассеяния, П – плотность потока мощности падающей электромагнитной волны. Если мы обозначим s – площадь плоской электромагнитной волны, то ее мощность
– мощности, теряемые падающей электромагнитной волной в результате поглощения и рассеяния, П – плотность потока мощности падающей электромагнитной волны. Если мы обозначим s – площадь плоской электромагнитной волны, то ее мощность  .
. , где находятся гидрометеоры и эти гидрометеоры находятся в объеме
, где находятся гидрометеоры и эти гидрометеоры находятся в объеме  (единичный объем), где N – количество частиц.
(единичный объем), где N – количество частиц. (1.1)
(1.1) (1.2)
(1.2) (2.1)
(2.1) (2.2)
(2.2) (3.1)
(3.1) (3.2)
(3.2)

 - удельный коэффициент поглощения (к 1 км)
- удельный коэффициент поглощения (к 1 км) - удельный коэффициент рассеяния (к 1 км)
- удельный коэффициент рассеяния (к 1 км)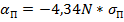 [дб/км]
[дб/км] [дб/км]
[дб/км]
 – эффективная плотность полного ослабления гидрометеорами электромагнитных волн
– эффективная плотность полного ослабления гидрометеорами электромагнитных волн ,
, – мнимая часть комплексного числа, m – комплексный коэффициент преломления,
– мнимая часть комплексного числа, m – комплексный коэффициент преломления,  – фазовое состояние гидрометеоров, для воды 0,333-0,112, для льда 9,6*10-4.
– фазовое состояние гидрометеоров, для воды 0,333-0,112, для льда 9,6*10-4. ,
, - для воды
- для воды  , для льда
, для льда  .
. ,
,  , это говорит о том, что при этих условиях ослабление только засчет поглощения.
, это говорит о том, что при этих условиях ослабление только засчет поглощения.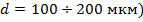 ,
, 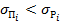 .
. ,
, г/м3, редко
г/м3, редко  г/м3.
г/м3.
 см, то
см, то  , где f(t) – некоторая функция, зависящая от температуры.
, где f(t) – некоторая функция, зависящая от температуры.
 ,
, дб/км.
дб/км. см,
см,  см.
см.

 , где
, где  - радиус гидрометеора.
- радиус гидрометеора.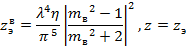

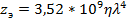 ,
, .
. ,
, – параметр, зависящий от интенсивности дождя,
– параметр, зависящий от интенсивности дождя, 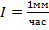 , то
, то  ;
;  , то
, то  .
. ,
, – скорость падения капель.
– скорость падения капель. и
и  :
: ,
, и
и  – эмпирические коэффициенты в зависимости от фазового состояния гидрометеора. Для жидких осадков
– эмпирические коэффициенты в зависимости от фазового состояния гидрометеора. Для жидких осадков  , где
, где  .
.
 .
. (10)
(10) ;
; 
 (11)
(11) (12)
(12) , и уравнение (12) запишем в виде:
, и уравнение (12) запишем в виде: (13)
(13)
 (14)
(14)
 ).
). [м-1] (15)
[м-1] (15) (16)
(16) (17)
(17) , то уравнение радиолокации метеообъектов (14) можно записать в следующем виде:
, то уравнение радиолокации метеообъектов (14) можно записать в следующем виде: (18)
(18) (метеорологический потенциал):
(метеорологический потенциал):
 (19)
(19) (20) – уравнение радиолокации, отдельные свойства оцениваются не с помощью
(20) – уравнение радиолокации, отдельные свойства оцениваются не с помощью  , а с помощью
, а с помощью  , тогда
, тогда (21).
(21). , и учтем коэффициент полезного действия антенно-волнового тракта (
, и учтем коэффициент полезного действия антенно-волнового тракта ( ), тогда метеорологический потенциал:
), тогда метеорологический потенциал:
 выразить в километрах, а отражаемость в [мм6/м3], то
выразить в километрах, а отражаемость в [мм6/м3], то
 (22)
(22) – чувствительность приемника радиолокационной станции.
– чувствительность приемника радиолокационной станции. .
. (23)
(23)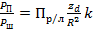 (24),
(24), – комплексный коэффициент, зависящий от длины волны и свойств окружающей среды.
– комплексный коэффициент, зависящий от длины волны и свойств окружающей среды. (25)
(25)


