
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 8. Уравнения Максвелла для электромагнитного поляСодержание книги
Поиск на нашем сайте
Согласно теории Максвелла для электромагнитного поля в случае нестационарных (то есть, изменяющихся во времени) электрического и магнитного полей, источниками электрического поля могут быть либо электрические заряды, либо изменяющееся во времени магнитное поле, а источниками магнитного поля могут быть либо движущиеся электрические заряды (электрические токи), либо переменное электрическое поле. В отличие от стационарных полей переменные электрическое и магнитное поля не являются независимыми друг от друга и рассматриваются как электромагнитное поле. Уравнения Максвелла, как система уравнений, описывающих природу происхождения и свойства электрического и магнитного полей в случае электромагнитного поля имеет вид: I. Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
II. III.
Суммарный ток проводимости I определяется в общем случае через поверхностную плотность тока j (
Ток смещения Iсм, пронизывающий поверхность S, определяется в общем случае через поверхностную плотность тока смещения Введенное Максвеллом понятие «тока смещения», величина которого определяется скоростью изменения вектора электрического смещения IV.
Таким образом, уравнения Максвелла для электромагнитного поля: I. III. Векторные характеристики электрического поля Векторные характеристики магнитного поля Кроме того, вектора плотности тока проводимости
где Уравнения Максвелла являются наиболее общими уравнениями для электрических и магнитных полей. Тема 9. Электромагнитные колебания в колебательном контуре Колебательный контур – это электрическая цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R. В идеальном колебательном контуре считается, что сопротивление R пренебрежимо мало (R» 0), что позволят в идеальном контуре (рис. 19),состоящем только изкатушки индуктивности и конденсатора, получить незатухающие электромагнитные колебания.
Рис. 19
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.66.147 (0.009 с.) |

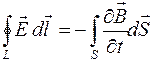 , то есть циркуляция вектора напряженности электрического поля определяется скоростью изменения вектора индукции магнитного поля
, то есть циркуляция вектора напряженности электрического поля определяется скоростью изменения вектора индукции магнитного поля  (
( - скорость изменения вектора индукции
- скорость изменения вектора индукции 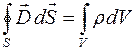 , то есть поток вектора электрического смещения
, то есть поток вектора электрического смещения  через произвольную замкнутую поверхность S, равен алгебраической сумме зарядов, заключенных внутри объема V, ограниченного данной замкнутой поверхностью S (r - объемная плотность заряда).
через произвольную замкнутую поверхность S, равен алгебраической сумме зарядов, заключенных внутри объема V, ограниченного данной замкнутой поверхностью S (r - объемная плотность заряда). , то есть циркуляция вектора напряженности
, то есть циркуляция вектора напряженности 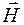 по произвольному замкнутому контуру L определяется полным током Iполн., пронизывающим поверхность S, ограниченную данным контуром L.
по произвольному замкнутому контуру L определяется полным током Iполн., пронизывающим поверхность S, ограниченную данным контуром L. - полный ток Iполн, складывающийся из тока проводимости I итока смещения Iсм., то есть Iполн. = I + Iсм..
- полный ток Iполн, складывающийся из тока проводимости I итока смещения Iсм., то есть Iполн. = I + Iсм.. ) интегрированием, то есть
) интегрированием, то есть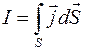 .
. (
( ) интегрированием, то есть:
) интегрированием, то есть:  .
. , показывает, что магнитные поля могут возбуждаться не только движущимися зарядами (электрическими токами проводимости), но и переменными электрическими полями.
, показывает, что магнитные поля могут возбуждаться не только движущимися зарядами (электрическими токами проводимости), но и переменными электрическими полями. , то есть поток вектора индукции
, то есть поток вектора индукции  и
и  связаны между собой следующим соотношением:
связаны между собой следующим соотношением: 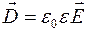 .
. связаны между собой следующим соотношением:
связаны между собой следующим соотношением: 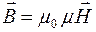 .
. и напряженности
и напряженности  , фигурирующие в уравнениях Максвелла, также связаны между собой:
, фигурирующие в уравнениях Максвелла, также связаны между собой: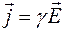 ,
, – удельная проводимость вещества.
– удельная проводимость вещества.



