Алгоритм решения системы линейных алгебраических неравенств

Отыскивать коэффициента распознающей линейной функции нейрона можно с помощью решения системы алгебраических неравенств. Пусть дана следующая таблица, причем значение y определяет класс которому принадлежит вектор

X1	X2	Y
		>=0
-1		>=0
		>=0
		>=0
		<0
		<0
		<0
		<0

 

По данной таблице запишем следующую систему неравенств:

2a₁ + 4a₂ >=0

-1a₁ + 3a₂ >=0

0a₁+1a₂ >=0

2a₁+5a₂>=0

3a₁+2a₂<0 (5)

6a₁+3a₂<0

a₁+a₂<0

4a₁+3a₂<0

 

Имеется проблема. Необходимо избавиться от строгих неравенств (> или <). В таком случае необходимо ввести малую величину E > 0, такую что c₁a₁+c₂a₂ <0 можно заменить на c₁a₁+c₂a₂ <= -E. Такая подстановка может привести к тому, что система не будет иметь решение.

 

Зададим E = 1 и приведем все неравенства к нестрогому виду

2a₁ + 4a₂ >=0

-1a₁ + 3a₂ >=0

0a₁+1a₂ >=0

2a₁+5a₂>=0 (6)

-3a₁-2a >=1

-6a₁-3a₂>=1

-a₁-a₂>=1

-4a₁-3a₂>=1

 

Неравенства с положительной правой частью называется невязкой. Если в системе нет невязок то и решение доставляется нулевыми значениями переменных. В противном случае описанный алгоритм пытается избавиться от невязок, при этом выделяют две фазы:

1. На первой фазе нужно получить систему базисных неравенств вида ai >=0

2. Вторая выполняется как и первая, но уже при наличии базисных неравенств

Если на второй фазе в процессе итераций встречается невязка, причем, все коэффициенты в левой части не положительны, то устанавливаем факт неразрешимости системы неравенств.

Пример:

Возьмем невязку -3a₁-2a >=1 и выведем из нее переменную a1:

a₁ <= -1/3 – 2/3a₂

a₁ = -1/3 – 2/3a₂ - z₁, z₁ – новая не отрицательная переменная (7)

подставим (7) в (6)

 

8/3a₂ – 2z₁= 2/3

11/3a₂+z₁>=-1/3

a₂>=0

11/3a₂-2z₁>=2/3 (8)

z₁>=a₂

a₂+6z₁>=-1

-1/3a₂+z₁>=2/3

-1/3a₂+4z₁>=-1/3

 

Первая фаза завершена и имется два базисных неравенства a₂>=0 и z₁>=0

Вторая фаза выполняется с небольшим отличием от первой: из невязки выражаем переменную с положительным коэффициентом, например, 8/3a₂ – 2z₁= 2/3:

Из 8/3a2 – 2z1= 2/3 выражаем a2

a₂>=1/4+3/4z1

a₂=1/4+3/4z₁+z₂ (9)

 

15/4z₁+11/3z₂ >= -5/4

3/4z₁+z₂ >= -1/4

3/4z₁+11/3z₂ >= -1/4

Z₁>=0 (10)

27/4z₁+z₂ >= -5/4

3/4z₁-1/3z₂ >= 3/4

15/4z₁-1/3z₂ >= -1/4

 

z₁ = 1+4/9z₂+z₃ (11)

 

Подстановка 11 приводит к системе невязок. В этой системе решение дает z₂=z₃ = 0; отсюда в силу подстановок 7, 9, 11 найдем a₁=-2, a₂=1.

При несовместности системы неравенств на некоторой итерации обязательно получится невязка, в левой части которой все коэффициенты будут либо отрицательны, либо нулевые.

 

Обучение нейронных сетей

Нейронные сети позволяет реализовать нелинейную распознающую функцию. Наиболее простую нейронную сеть представляет персептрон. Персептрон – сеть прямыми связями, состоящая из трех слоев: входного, промежуточного и выходного.

S = ∑(a_i*x_i),

ai – входные сигналы из нижестоящих слоев на вход верхним.

Процесс обучения состоит в следующем:

На входной слой подают образцы сигналов 0 или 1, для которых известны реакции выходного слоя. Если выходной слой отреагировал нерпавильно, то для каждого выходного элемента вычисляется сигнал ошибки.

b’j = y’_j*(d_j-o_j) (2)

(d_j-o_j) – Разность между ожидаемым и фактическим сигналом на выходе нейрона

y'_j – значение производной выходного сигнала j-го элемента выходного слоя

Для получения сигнала на выходе и в промежуточном слое используют так называемую сигмоидальную функцию на выходе нейрона. Такая функция имеет следующий график:

S – вычисляемая сумма, y – значение выходного сигнала получаемого по формуле:

y = 1/(1-e^-s) (3)

S= 0 y=0.5; S->+∞

dU(x)/dV(x) = (U’v – V’U)/ V²

y’= dy/dS = e^-s/(1+e^-s)² =y(1-1/*1+e^-s)) = y(1-y) (4)

После того как для выходных нейронов найдены сигналы ошибок, для каждого выходного нейрона вычисляется изменение веса связью от нейрона предыдущего слоя по формуле:

W_zj = n*b_j*y_z b_j – сигнал ошибки j-го выходного нейрона, yz – выходной сигнал от предыдущего нейрона z, поступающий на вход нейрона j, n – коэффициент регулирующий скорость обучения (обычно = 1)

С выходным слоем разобрались. Сигнал ошибки нейрона, находящегося в промежуточном слое, определяется от вышестоящих нейронов с которыми он связан

b_z = y’_z ∑b_jW_zj (7)

Веса вычисляются по формуле 5.

Описанный алгоритм получил название «Обучение на основе обратного распространения ошибки».

Пример

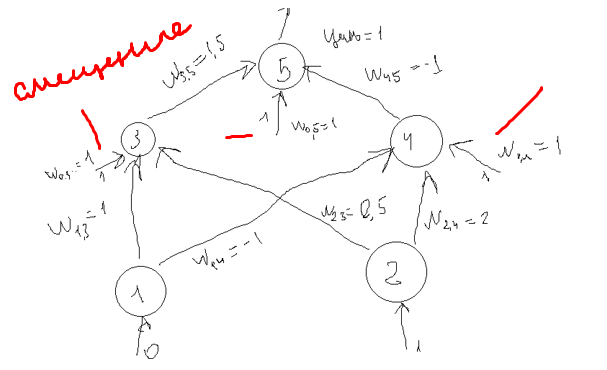
На вход подаем 0 и 1, нейрон 5 выходной, 3,4 – скрытый слой. Выходная функция нейрона 3:

S₃=w_0,3(1) + w_1,3*0 + w_2,3*1 = 1*1+1*0+0.5*1 =1.5.

От этого значения вычисляется сигмоидальная функция:

U3 = y(1.5) ~= 0,817 из формулы 3.

 

S₄ = w_0,4*1+w_2,4*1+w_1,4*0 = 1*1+ (-1 * 0) + 2 * 1 = 3

U₄ = y (3) ~= 0.952 из формулы 3

S₅ = w_0,5*1 + w_3,5 * U₃ + w_4,5 * U₄ = 1*1 +1.5*0.817+ (-1*0.952) = 1,27

U₅ = y(1,27)~= 0.781 из формулы 3

Правильный сигнал на выходе пятого нейрона должен быть равен 1. Т.к. мы получили значение < 1 производим коррекцию. Вычисляем сигнал ошибки по формуле:

₅= y’₅(d₅-o₅) = y₅ (1-y₅) * (d₅-o₅) = 0.781* (1-0.781) * (1-0.781) = 0.037

Далее находим сигнал ошибок от нейронов 3 и 4 по формуле 7.

₃= y’3 * ∑ ₅*w_3,5 = u₃*(1-U₃) * ₅*1,5 = 0,0083

₄= y’4∑ ₅*w_4,5 = U₄(1-U₄) * ₅* (-1) = 0,952 * (1-0,952) *0,037* (-1) = -0,0017

Далее пересчитываются веса связей (W_zj). Примем £ = 0.5

W_3,5 = w_3,5 + £* ₅+U₃ = 1,5 + 0.5*0.037 * 0.817 = 01.525

W_4,5 = w_4,5 + £* ₅* U4 = -0.982

W_0,5= w_0,5+£*Смещени5 = 1,052

Далее производим коррекцию весов w_1,3 w_2,3 w_1,4 w_2,4. Для примера рассмотрим только коррекцию веса w_2,3:

W_2,3 = W_2,3+£* *U₂ = 0.5 + 0.5*0.0083 *1 = 0.504

И так далее по аналогии…

Семантическая обработка текста. Проблема поиска по ключевым словам

При работе с текстом как с базой знаний мы имеем дело с текстом как с семантическим объектом. С такой базой знаний следует организовать интерфейс. Интерфейс предполагает обработку вопросов, организацию контекстной помощи, тестирования знаний и т.д. Семантический вопрос требует выдачи точного или точечного ответа.

Чтобы обеспечить семантическую обработку вопросов текст следует представить в формализованном виде. Здесь имеется несколько способов, например, в виде семантической сети, прямолинейный подход. Основные задачи, решаемые при работе с текстом – распознавание и классификация. Как правило любой текст можно охарактеризовать набором ключевых слов. Когда имеется множество текстовых документов со своими ключевыми словами то возникает проблема построения поискового дерева, которое позволяет отыскивать требуемый документ с незначительными временными издержками.