Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель знаний на основе фреймов.Содержание книги
Поиск на нашем сайте Фреймы предложены Марвином Минским. Минский ввел терминологию и язык фреймов включающий понятия фрейма, слота, значение по умолчанию и т.д. Фрейм имеет следующую структуру: {<Имя фрейма> <Имя слота 1><Значение слота1> … <Имя слота n> <Значение слота n>}. В качестве примера рассмотрим пример выбор скорости автомобиля: { <выбор скорости> <состояние дороги>: 0.6 <состояние машины >: 0.8 <состояние водителя>: 0.5 } Наша ЭС должна определять оптимальную скорость автомобиля с учетом состояния дороги, машины и водителя. Так как в данном примере уже указаны значения слотов, то необходима процедура оценки скорости по данным значениям слотов, такая процедура называется демоном. На ряду с процедурами демонами используются процедуры слуги, которые используются для установления значения слотов. Фрейм из примера называется конкретным фреймом. А фрейм с неопределенным значением слотов называется фреймом прототипом. {<состояние дороги> <состояние покрытия>: 0.5 <видимость>: 10
… } Ясно что для организации экспертной оценки скорости требуется создать все необходимые фреймы и разработать процедуру комплексной оценки, например, используя метод СААТИ. Семантические сети. В реальном мире любую ситуацию можно охарактеризовать следующим образом: 1. Указать какие объекты участвуют в ситуации 2. В какие отношения вступают объекты 3. Указать свойства объектов и свойства отношений, таким образом можно передать знания в очень широком классе ситуаций. Рассмотрим пример. «Студент Максимов сдал экзамен по химии.» В этой ситуации выделяем объекты Максимов и экзамен. Отношение между объектами передаются с помощью глаголов, в данном случае – сдать. Свойство Максимова является «студент». Свойством экзамена является по химии. Свойством отношения сдать является время и характер действия, в данном случае это прошедшее время.
Кто?
Какой? Какой?
Объекты, отношения и свойства отображаются различными видами вершин. Ситуации могут образовывать целые сценарии. Например: «Экзамен по химии принимал профессор ZZZ».
>
Структуру семантической сети можно представить на языке XML и обработать программно. Семантические сети – граф, вершинами которого являются объекты и понятия, а дуги связывающие вершины определяют отношения между ними. Понятие логического вывода[EB2] Основной задачей любой логической системы является построение логического вывода. Это касается как классической, так и не классической логики. Для того чтобы строить выводы нужно иметь правила вывода, а сами формулы должны быть приведены к удобному для вывода виду. В этом смысле наиболее удобно представление логических формул в виде дизъюнктов. Определения из предыдущей лекции. [EB3] Правилом вывода R называется такое соотношение между формулами A1, A2,.. An и B, которое устанавливает истинность формулы B всякий раз когда выполняется заданное соотношение. Формула B выводима из формулы A1, A2,..An если имеется конечная последовательность формул П, начинающихся с любой из формул Ai, такая, что очередная формула этой последовательности либо выводима по некоторому правилу вывода из предшествующих членов (или их части) или совпадает из какой-то из формул Ai. Всякая тождественно истинная формула выводима. Задача логического вывода в логике высказываний может сводиться к задаче на выполнимость. Пусть даны дизъюнкты D1, D2,.. Dn. Спрашивается, выводим ли из них дизъюнкт R, т.е. требуется установить тождественную истинность формулы D1 & D2 &.. & Dn -> R. Умножим левую и правую часть на не R. Получим D1 & D2,.. &Dn & R -> FALSE. Если удастся показать выполнимость данного уравнения то получим опровержение данной формулы, т.е. R не выводима. Если не выполнима то исходная формула выводима. Таким образом задача логического вывода сводится к задаче выполнимость. Пример Пусть даны следующие формулы f1 = a -> bc a(a->bc S -> FALSE – невыводимость
Законы логики высказываний[EB4] Привести к виду дизъюнктов следующую формулу: Сложнее дело обстоит в логике предикатов. Такое приведение выполняется в 3 этапа. На первом этапе все кванторы вынося в начало формулы, например, *логическая формула*. Вынесение кванторов даст следующий результат *логическая формула 2*. Однако имеется все же одна зацепка. Изменим формулу следующим образом *логическая формула 3* (2 квантора существования связанных с одним и тем же y. Необходим переход к новым обозначениям, от которых формула не теряет своей тождественности). Получаем *логическая формула 4*. На втором этапе отбрасывают кванторы. Здесь имеется специфика в отношении кванторов существования. Так в формуле *логическая формула 5* берут самый внутренний квантор существования т.е. (СУЩ(t)) и заменяют переменную t на произвольную функцию от предшествующих переменных кванторов всеобщности, а сам квантор существования отбрасывают. Например, из *логическая формула 5* получаем *логическая формула 6*. Тоже самое делают с квантором существования y, но используя другую функцию. * логическая формула 7*. Приведенная процедура избавления от кванторов существования называется сколемизацией (фам Scolem). Теперь, когда кванторов существования не осталось, кванторы всеобщности просто отбрасывают и получают P(x,h(x)) ->Q(x,f(x)) На третьем этапе получаем дизъюнкты на основании законов Де Моргана получаем:
Здесь отрицание последовательно перемещается по формуле, при этом очередной квантор всеобщности заменяется на квантор существования и наоборот. В конце концов отрицание добирается до самой формулы. После это проводим сколемизацию. Также обращаем внимание на то, что первому квантору существования не предшествует ни один квантор всеобщности. В этом случае переменная x заменяется на произвольную константу c. В качестве универсальных правил вывода в логике можно отметить следующие: 1. Правило исключения 2. Правило приведения к абсурду В логике широкое распространение получил метод вывода на основе принципа резолюций Джона Робинсона. Машина вывода в логике. Понятие машины вывода Машина вывода – механизм отыскания решения задачи (алгоритма решения). Машина вывода в логике строит логическое доказательство. В основе машины вывода лежит теорема дедукции. Вывод строится согласно определенным правилам. Наиболее общим из них является доказательство от противного, т.е. x i заменяют на xi и приводят к противоречию. Доказательство от противного формулируется в виде следующей известной теоремы о дедукции и записывается следующим образом Бз/х = (Бз &
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 , f2 = b->
, f2 = b->  f, f3 = cv
f, f3 = cv  . Получаем
. Получаем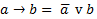

 В итоге получили ситуацию FALSE-> FALSE, следовательно, выводимость имеет место.
В итоге получили ситуацию FALSE-> FALSE, следовательно, выводимость имеет место.