
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие эвристической оценочной функции. Оценка состояний на дереве эвристического поиска
Машина вывода может использовать механизм эвристического поиска на дерев состояний задач (которое также называют деревом решения). Рассмотрим игру в крестики нулики с исходным состоянием S0 S0
S1
S2
Выбор S1 или S2 осуществляется на основе эвристической функции, предложенной Нильсоном 1. <S0, Sf,A,Ra,Rs> a. S0 – исходное состояние системы b. Sf – искомое состояние системы c. A – алгоритм отображения S0 - > Sf d. Ra – ограничение на алгоритм e. Rs – ограничение на состояние Состояние Si непосредственно достижимое из состояния Sk называется приемлемым, а Sk- предшественник Si. Граф G(S, Pi) со множеством вершин состояний Sj принадлежащих S и дуг Pi связывающих предшественников и приемников образует дерево решений с корнем S0 и листом Sf, если: 1. Мю -й ярус в графе образует те приемники (мю – 1) яруса, которые не входят в ярусы (мю -2,3,..) 2. Листьями в графе G являются состояния, все предшественники которых содержаться в верхних ярусах за исключением Sf Задачи машины вывода состоит в отыскании пути из S0 в Sf. Любая часть этого пути называется трассой вывода. Для построения трассы вывода используют механизм оценочных эвристических функций. Примером такого алгоритма является алгоритм Нильсона (алгоритм А*). Качество эвристических оценочных функций определяется тем, на сколько близко создаваемая алгоритмом трасса вывода держится оптимальной. Например, можно использовать оценку K = L/T, T – Общее число вершин, пройденных в дереве решений, L – длина оптимального пути из S0 в Sf. Определим эвристическую оценочную функцию следующим образом F(n) = g(n) + h(n), f(n) – значение эвристической оценочной функции в вершине Sn, g(n) – оценивает затраты произведенные в вершине Sn из вершины S0, обычно измеряются длинной пути из Sn в S0. Для нашей игры g(n) учитывает число пройденных вершин, h(n) – Оценивает будущие затраты, для нашей игры тем лучше, чем больше выйгришных ситуаций оставляет данная позиция для реализации.
Выбор функции h(n) как числа выигрышных комбинаций не точен, т.к. h(n) должна учитывать не только число выигрышных комбинаций но и возможность их построения, т.е. способность противника часть из них. Таким образом, более точно учитывать не только число выигрышных комбинаций но и количество шагов для завершения каждой из них. На практике значение h(n) заменяют ее оценкой Задача коммивояжёра Рассмотрим алгоритм Нильсона на примере зада коммивояжера (или же «бродячего торговца»). Пусть имеется n городов, соединенных дорогами
Введем матрицу затрат C[Cij]
В задаче требуется найти цикл с минимальной суммой затрат из образующих его дуг, которые проходят каждую вершину не более одного раза, за исключением вершины из которой цикл начинается и в которой заканчивается. Для данного метода эвристического поиска применяется способ оценки H(n) предложенный Литтлом, Мерти, Суини. Для этого способа нужно на текущей матрице расстояний сначала найти минимальный элемент в каждой строке, затем найденные элементы вычитают из соответствующих элементов строки.
Далее отыскивают минимальные элементы в столбцах и вычитают их из соответствующих столбцов
Затем находим сумму минимальных элементов в столбцах и строках: 1+0+0+5+2+1+3 = 12. Это и есть способ оценки ^h(n). Эта величина определяет нижнюю границу для любого цикла в сети, следовательно, по какому бы циклу мы не пошли его длинна не может быть меньше 12. Для каждого состояния (вершины) будем рассматривать два продолжения: одно соответствует включению некоторой дуги в искомое решение, а другое исключение.
Например, начнем движение из вершины 3 и выберем дугу 3->4.
g1 = 8 g2=0 Начнем оценку с вершины S1, Она соответствует включению дуги в оптимальное решение. Состояние S1 следует модифицировать матрицу расстояний следующим образом: все значения в строке 3 и столбце 4 следует заменить на бесконечность, а саму ячейку [3,4] заменить на 0.
Опять находим минимальные значения в строках и столбцах, и вычитаем
h(n) = 5+3+3 =11; f(n) = Теперь рассмотрим состояние S2. В это состояние мы попали без затрат. На матрице расстояний надо установить C[3,4] = ∞
Опять находим минимумы в строках и столбцах
g(2) = 0; f(2) = 12 + 0 = 12
При выполнении эвристического поиска следует всегда двигаться из вершины с наименьшим значением эвристической функции, если решается задача на минимум. Поэтому продолжаем движение из вершины S(2).
Находим минимумы в строках и столбцах
g(3) = 2; f(3) = 10 + 2 = 12
Теперь оценим вершину S4
g(4) = 0 f(4) = 12 + 0;
Теперь для продолжения можно использовать любое из состояний S3 или S4, например возьмем состояние S4. Ясно, что теперь мы должны двигаться в вершину 2, т.е. выбрать переход C[3,2], т.к. дргуих не остается. Наш граф примет следующий вид
^h(5) = 6+2+0+3+1 = 12 g(5) = 1 f(5) = 12 + 1 = 13;
Описанный процесс рано или поздно приведет нас в конечную вершину с некоторым решением (найденным циклом) Пусть нами найдено следующее решение Sf [(3,1); (1,4); (4,2); (2,3)] проиллюстрируем принцип отсечения в действии. Ранее мы нашли значение эвристической функции в S1(f(1) = 19), а Sf(f(F) = 17). т.к. 19 > 17 движение из S1 блокируется, т.к. при движении из нее эвристическая оценочная функция может только возрастать, хотя этот факт еще требует доказательства. Доказательство этого факта основано на монотонности, которая заключается в том, что для любых двух вершин, лежащих на одном пути. Более нижняя вершина должна иметь значение эвристической функции не меньшее у более верхней вершины.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.19.251 (0.029 с.) |
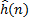


 + g(n); f(1) = 11 + 8 = 19;
+ g(n); f(1) = 11 + 8 = 19; = 5+2+1+3+1 = 12;
= 5+2+1+3+1 = 12;
 = 5+2+3 = 10;
= 5+2+3 = 10; = 5+2+1+3+1 = 12;
= 5+2+1+3+1 = 12;



