Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Продукционная модель знаний.Содержание книги
Поиск на нашем сайте Логическая модель знания Логические модели наиболее универсальны и формализованы. Для них имеется мощный математический аппарат. Логическая модель представляет собой конечное или бесконечное множество логических формул, называемых предикатами. Для записи формул используют язык, содержащий алфавит (набор символов) и множество правил образования правильно построенных формул. Символами логического языка являются: 1. Константы: 0, 1,2 … или ‘a’, ‘b’, ’c’ 2. Переменные: x, y, z 3. Функциональные символы (функторы): f, g, h, … 4. Символы предикатов (отношений): P, Q, R 5. Кванторы: всеобщности и существования 6. Логические операции (связки): &- и, v – или, - не Кроме символов языка рассматриваются также синтаксические правила записи формул или предложений логического языка. Отправным элементом здесь является предикат – простейшая формула (атомарная формула) принимающая два значения: истина или ложь; вида P(..), где в скобках указываются аргументы предикаты: переменные, константы или же функторы. Каждый предикат есть формула логического языка. Путь P и Q – любые две формулы, тогда формулами также являются: 1. P Q 2. P v Q 3. P & Q 4. P -> Q 5. P <- Q 6. …P(x) 7. …X P(x)
Таблицы истинности
Дизъюнктом (в логике высказываний) называется дизъюнкция литер (булевских переменных) с отрицаем или без него вида: x v y v z Дизъюнктом в логике предикатов называется дизъюнкция литералов (атомарных формул) взятых с отрицанием или без него вида: P(a, z) v Q(z, f(x)) Конъюнктивной нормальной формой (КНФ) называется конъюнкция дизъюнктов. Выполняющей интерпретации I для заданной КНФ называется множество значений переменных, при которых она истинна, например: I = (x1 v x2) & (x2 v x3) & (x1 v x3) Число различных интерпретаций для дизъюнкта с n > 0 переменными = 2n, Однако не все они являются выполняющими. Задача на выполнимость формулируется так: Для данной КНФ установить имеется ли для нее хотя бы одна выполняющая интерпретация. Формула B следует из формулы A – если в любой интерпретации где А истина B также истина (A -> B). Формула A тождественно истинна если она истинна в любой интерпретации (x v Рассмотрим пример построения логической модели. Пусть имеется множество работ и множество работников. Необходимо назначить каждому работнику ровно 1 работу так, чтобы все работы были распределены. R1-R5 – работы. A1-A5 - работники
X11 + X13 + X15= 1 X21 + X24 = 1 X31 = 1 X44 + X45 = 1 X52 + X53 = 1 По работникам
X11 + X31 = 1 X22 + X52 = 1 X13 + X53 = 1 X24 + X44 = 1 X15 + X45 = 1 По работам
Продукционная модель знаний. Продукционная модель представляет собой вариант логической модели, записанной с помощью продукционных формул или правил вида: F -> G (1) (если F то G), где F и G – произвольные логические формулы. Отмечается, что продукции «более близки» по форме естественным умозаключением вида «если – то» (Если идет дождь – возьмите зонтик. На практике общее условие 1 можно рассматривать в виде формул так называемого секвинционального вида: f1 & f2 &.. fn -> g1 v g2 v.. gz (2). Система логического программирования PROLOG использует еще более упрощенные секвенциональные формулы (так называемою нотацию Корна): f1 & f2 &.. & fn -> g (левая часть тело продукции, правая голова или цель). В ПРОЛОГе имеется 3 вида предикатов: 1. Стандартные предикаты. Предикаты которые всегда истины и не объявляются в разделе predicates (write, readchar, nl) 2. Предикаты факты. «Алексей мечтает о деньгах и карьере». На прологе Мечтает(Алекскй, деньги). Мечтает(Алекскй, карьера). Факты – особый вид правил которые не нужно доказывать. Такие правила представляют собой продукции без головы. Аргуметами предикатов фактов являются константы. 3. Предикаты правила. «Владимиру нравится все, что нравится Ире. На ПРОЛОГе: Нравится(Владимир, Х): - Нравится(Ира, Х). Нравится(Ира, Х) -> Нравится(Владимир, X) a: -b, c, d. b & c & d -> a» Семантические сети. В реальном мире любую ситуацию можно охарактеризовать следующим образом: 1. Указать какие объекты участвуют в ситуации 2. В какие отношения вступают объекты 3. Указать свойства объектов и свойства отношений, таким образом можно передать знания в очень широком классе ситуаций. Рассмотрим пример. «Студент Максимов сдал экзамен по химии.» В этой ситуации выделяем объекты Максимов и экзамен. Отношение между объектами передаются с помощью глаголов, в данном случае – сдать. Свойство Максимова является «студент». Свойством экзамена является по химии. Свойством отношения сдать является время и характер действия, в данном случае это прошедшее время.
Кто?
Какой? Какой?
Объекты, отношения и свойства отображаются различными видами вершин. Ситуации могут образовывать целые сценарии. Например: «Экзамен по химии принимал профессор ZZZ».
>
Структуру семантической сети можно представить на языке XML и обработать программно. Семантические сети – граф, вершинами которого являются объекты и понятия, а дуги связывающие вершины определяют отношения между ними. Понятие логического вывода[EB2] Основной задачей любой логической системы является построение логического вывода. Это касается как классической, так и не классической логики. Для того чтобы строить выводы нужно иметь правила вывода, а сами формулы должны быть приведены к удобному для вывода виду. В этом смысле наиболее удобно представление логических формул в виде дизъюнктов. Определения из предыдущей лекции. [EB3] Правилом вывода R называется такое соотношение между формулами A1, A2,.. An и B, которое устанавливает истинность формулы B всякий раз когда выполняется заданное соотношение. Формула B выводима из формулы A1, A2,..An если имеется конечная последовательность формул П, начинающихся с любой из формул Ai, такая, что очередная формула этой последовательности либо выводима по некоторому правилу вывода из предшествующих членов (или их части) или совпадает из какой-то из формул Ai. Всякая тождественно истинная формула выводима. Задача логического вывода в логике высказываний может сводиться к задаче на выполнимость. Пусть даны дизъюнкты D1, D2,.. Dn. Спрашивается, выводим ли из них дизъюнкт R, т.е. требуется установить тождественную истинность формулы D1 & D2 &.. & Dn -> R. Умножим левую и правую часть на не R. Получим D1 & D2,.. &Dn & R -> FALSE. Если удастся показать выполнимость данного уравнения то получим опровержение данной формулы, т.е. R не выводима. Если не выполнима то исходная формула выводима. Таким образом задача логического вывода сводится к задаче выполнимость. Пример Пусть даны следующие формулы f1 = a -> bc a(a->bc S -> FALSE – невыводимость
Законы логики высказываний[EB4] Привести к виду дизъюнктов следующую формулу: Сложнее дело обстоит в логике предикатов. Такое приведение выполняется в 3 этапа. На первом этапе все кванторы вынося в начало формулы, например, *логическая формула*. Вынесение кванторов даст следующий результат *логическая формула 2*. Однако имеется все же одна зацепка. Изменим формулу следующим образом *логическая формула 3* (2 квантора существования связанных с одним и тем же y. Необходим переход к новым обозначениям, от которых формула не теряет своей тождественности). Получаем *логическая формула 4*. На втором этапе отбрасывают кванторы. Здесь имеется специфика в отношении кванторов существования. Так в формуле *логическая формула 5* берут самый внутренний квантор существования т.е. (СУЩ(t)) и заменяют переменную t на произвольную функцию от предшествующих переменных кванторов всеобщности, а сам квантор существования отбрасывают. Например, из *логическая формула 5* получаем *логическая формула 6*. Тоже самое делают с квантором существования y, но используя другую функцию. * логическая формула 7*. Приведенная процедура избавления от кванторов существования называется сколемизацией (фам Scolem). Теперь, когда кванторов существования не осталось, кванторы всеобщности просто отбрасывают и получают P(x,h(x)) ->Q(x,f(x)) На третьем этапе получаем дизъюнкты на основании законов Де Моргана получаем:
Здесь отрицание последовательно перемещается по формуле, при этом очередной квантор всеобщности заменяется на квантор существования и наоборот. В конце концов отрицание добирается до самой формулы. После это проводим сколемизацию. Также обращаем внимание на то, что первому квантору существования не предшествует ни один квантор всеобщности. В этом случае переменная x заменяется на произвольную константу c. В качестве универсальных правил вывода в логике можно отметить следующие: 1. Правило исключения 2. Правило приведения к абсурду В логике широкое распространение получил метод вывода на основе принципа резолюций Джона Робинсона. Машина вывода в логике. Понятие машины вывода Машина вывода – механизм отыскания решения задачи (алгоритма решения). Машина вывода в логике строит логическое доказательство. В основе машины вывода лежит теорема дедукции. Вывод строится согласно определенным правилам. Наиболее общим из них является доказательство от противного, т.е. x i заменяют на xi и приводят к противоречию. Доказательство от противного формулируется в виде следующей известной теоремы о дедукции и записывается следующим образом Бз/х = (Бз & Метод Ковальского …. Здесь для каждого дизъюнкта строят вершину и соединяют ребрами по контрарным парам переменных. Резольвенты строят таким образом: выбирают любое ребро связывающее 2 литеры (x1 и не x1) строят резольвенту дизъюнктов D1 и D2 по контрарной паре литер, добавляем резольвенту в форме новой вершине графа, а ребро (x1, не x1) удаляем, при этом действуют следующие правила: 1. Если имеется вершина в которой действует не соединенная с другими буква, то такая вершина удаляется со всеми несоединенными ребрами 2. Произвольно выбираем ребро и находим резольвенту по 2 вершинам данному ребру, добавляем резольвенту в граф и соединяем ее с другими вершинами, поле чего выбранное ребро удаляем из графа. Тавтологические дизъюнкты удаляем. 3. Вершины резольвенты связываются связями с другими вершинами по контрарным литерам 4. Если в графе Ковальского получены две вершины xi и не xi то говорят о противоречии и процесс завершается 5. Если граф Ковальского удается полностью разрушить без получения противоречия, то это говорит о том, что система не противоречива. Метод отсечения литер Дизъюнкты: …. Основная идея: удалить из системы последовательно все литеры (буквы), одну за другой. Если в процессе удаления получаем противоречие, то как и в графе Ковальского, получаем что система не имеет решения. Включим в новую систему все формулы, представляющие собой резольвенту по x1
Базовые [EB5] понятия ПРОЛОГ 1. Прикладные системы на языке Prolog. Роль языка Prolog. Сферы применения пролога – транспорт, логистика, анализ месторождений полезных ископаемых, оценка загрязнений окружающей среды, Системы с естественно-языковым интерфейсом, НАСА использует голосовой Пролог для управления голосом аппаратурой. 2. Базовые понятия и структура программы Предикат является основой концепцией пролога. Предикат – логическая формула, с произвольным числом аргументов (их может и не быть вовсе), который принимает 2 значения: истинна или ложь. На прологе используют 3 вида предикатов: 1. Предикаты факты – используются для записи некоторых утверждений, которые в ходе выполнения программы считаются истинными. В конце предиката факта в конце обязательно ставится точка, аргументами фактов являются константы. Набор фактов на прологе называется базой данных 2. Предикаты правила 3. Стандартные предикаты. Входят в состав самого пролога и считаются истинными(write(X) – вывод на экран, nl – переход на новую строку Правила и факты называются клозами или же предложениями. Переменные записываются с большой буквы, константы с маленькой. Если предикат состоит из нескольких клозов, то они должны быть расположены вместе, подряд. Стандартные типы данных 1. Integer 2. Char 3. String 4. Real 5. Symbol 6. Etc. Структура программы и назначение секций: Программа на прологе состоит из 4-х секций: 1. Domains 2. Predicates 3. Goal 4. Clauses В секции predicates происходит объявление не стандартных предикатов, т.е. пользовательских. Объявление происходит через ключевое слово nondeterm. Секция domains содержит объявление нестандартных типов данных: списки, функторы, тут могут быть и пользовательские типы. Секция goal. Здесь задается целевой предикат программы или последовательность предикатов, которые надо доказать. Секция clauses содержит доказательство целевого предиката. Выполнение программы на прологе заключается в доказательстве целевого предиката. Этот предикат является обычным правилом. Чтобы доказать правило (любое, а не только цель), необходимо доказать все предикаты, входящие в его тело. Для этого происходит согласование предикатов, с другим одноименным предикатом, т.е. сопоставление (унификация) соответствующих аргументов этих предикатов. При унификации аргументов возможные следующие случаи: 1. Сопоставление двух констант заканчивается успешно, если они равны, и неудачно в противном случае. 2. Сопоставление константы и переменной (свободной, не имеющей значения) заканчивается успешно и переменная получает значение константы (становится связанной) 3. Сопоставление двух связанных переменных: сопоставление заканчивается успешно если переменные равны и неудачно в противном случае. Одна из переменных связана – другая свободна: заканчивается успешно и свободная переменная принимает значение связанной; Сопоставление двух свободных переменных успешно, если в последствии одна из переменных получает значение, то и другой переменной присваивается тоже значение. Если согласование предикатов закончилось неудачно, то делается попытка согласования данного предиката с другим одноименным клозом. Если таких клозов нет, то происходит возврат (Back tracking) к ближайшей развилке. Пусть некто сообщает, что он задумал шифр из 5-ти двузначных цифр. Обозначим их как X1,.., X5. При этом задаются следующие соотношения между цифрами. При этом X2+X3+X4<=2, X2+x4+X5 <=1, X3+X4+X5>=1; X1+X5<=1 Пример
Данная программа состоит из 3х секций. В секции predicates объявлены 2 предиката: equation and znach. В секции goal задается целевой предикат equation. В clauses происходит непосредственно доказательство результата equation. Для того чтобы доказать целевой предикат, система выбирает первое условие из определения предиката- znach(X1). Пролог пытается доказать это условие и ищет его определение в разделе clauses. Такое определение имеется. Происходит унификация или же согласование аргументов предикатов, т.е. X1 согласовывается с B. Т.к. B = 0, то и X1 Получает значение 0. Аналогично доказываются предикаты znach(X2 -X5). Далее выполняется проверка условий, однако X3 + X4 +X5 >=1 условие не выполняется, поэтому в силу вступает механизм ветвления-возврата. Система возвращается в точку последнего ветвления, т.е. Znach(X5). На этот раз пролог сопоставит Znach(X5) и Znach(B): B=1. Znach(X1-X4) по-прежнему нули, и вновь выполняем проверку условий. Если все успешно, то происходит вывод на экран. Предикат fail Инициирует неудачу в доказательстве. Пролог начинает поиск с возвратом, когда доказательство какого-либо предиката завершается неудачей. Определенной ситуации бывает необходимо инициировать поиск с возвратом, чтобы найти другое решение, для этого используется специальный предикат FAIL – неудача.
Программа требует найти отца Y. Fail делает доказательство всегда неудачным. Для того, чтобы вывести все решения в теле предиката everebody поставили команду fail. После того как на экран выводится значение переменных x=leonard, y=Katerina, возникает состояние искусственной неудачи (fail). Происходит возврат к ближайшей развилке, т.е. father(X,Y), т.к. этот предикат не сопоставлялся с двумя оставшимися факторами. При этом переменные X и Y становятся свободными. Теперь предикат father(X,Y) сопоставляется с фактом father(karl, nick). Переменные X, Y получают соответствующие значения и далее вывод осуществляется по аналогии. Механизм отсечения Пролог использует отсечения для прерывания поиска с возвратом. Обозначается как «!». Пройдя через отсечение уже невозможно произвести откат к предикатам, расположенным в обрабатываемом предложении перед отсечением, а также невозможно возвратиться к другим предложениям. Определяющим данный предикат.
Если с завершится неудачей, то пролог не сможет произвести откат (поиск с возвратом) через отсечение и найти альтернативные решения для а и b. Он также не сможет обратиться к другому предложение предиката r1.
В данном примере необходимо найти корвет конкретного цвета и подходящего по цене. Пролог обращается к предикату car и проверяет первую машину, она не подходит, и мы берем следующий предикат, находим предикат колорс. Наконец мы проходим через отсечение, которое, замораживает. Все переменные, ранее связанные в этом предложении. Переходим к сравнению прайс меньше 25000. Проверка завершается неудачно, т.к. Прайс = 26000, и пролог пытается совершить перебор с возвратом, для того, чтоб найти другую машину, однако отсечение не даст этого сделать и наше целевое утверждение завершается неудачно. Рекурсия Рекурсия – вызов предиката из тела самого предиката. Рекурсия обычно применяется при обработке списков в программах на прологе. Пример:
Программа требует найти предмет который нравится Петру. Первый клоз заканчивается FALSE, т.к. не совпадают константы. Второй заканчивается тру и X сопоставляется с Z. Z и X получают значение carrot. Изменим программу следующим образом:
Как и ранее программа требует найти то, что нравится Пете, однако теперь логика программы изменена. Пете нравится то, что не нравится Джону. Это факт мы переделали следующим образом: like(peter,Z):- not(like(Jhon,Z)). Отрицание передают предикат not, однако, следует помнить, что данные предикат не может использоваться в голове правила, т.е. недопустимо: not(like(peter,Z)):-like(Jhon,Z). Однако имеется и второе ограничение: в момент вызова предиката с отрицанием аргументы предиката уже должны иметь значения. В этом случае пролог выдаст сообщение об ошибке. Переделаем программу следующим образом:
В znach поместили carrot, доказываем like(Jhon,carrot). Доказали его в первом клозе. Далее вернулись в правило, а там стоит предикат not(like(Jhon, carrot)), отрицание истины дает ложь, следовательно, откатываемся до ближайшей развилки, а именно предиката znach, и заносим в переменную Z значение candies. Далее снова доказываем предикат like(Jhon, candies). Доказали его во втором клозе. Заходим во второй, клоз, унификация проходит успешно, однако там стоит предикат fail, который инициирует неудачу в доказательстве, следовательно предикат like(Jhon,candies) заканчивается ложью. Возвращаемся в правило, not(like(Jhon,candies)) = true (отрицание лжи = истина). Таким образом предикат like() доказан, и соответственно цель (goal) доказано, а X принимает значение candies.
Z- начальное значение, N – промежуточное (накапливаемое), M – окончательное. N=1 N1=3 Z1=2 Fact(2,3,M) N1=6 Z1= 1 Fact(1,6,M) M=N // M= 6;
Fact(3,M) N =3 N1=2 Fact(2,M1) M=2 N1=1 Fact(1,M1) Fact(1,1) M=M1*N // M=1*2 = 2 M=M1*N // M = 2*3 =6
Сложные структуры данных в прологе. Функторы и списки Список представляет собой последовательность из произвольного числа элементов, некоторого типа. Списки необходимо определять в секции domains следующим образом:
Где тип – тип элемента списка. Он может быть, как стандартным, так и не стандартным, т.е. заданным пользователем и объявленным в разделе domains ранее. Пример
Кроме того, элементами списка могут быть не только числа, но и строки, а также и сами списки, например:
Ввод списка с клавиатуру осуществляется через readterm(<тип>m <имя переменной>), где тип – списочный тип, который предварительно должен быть объявлен в разделе domains. Вывод списка на экран осуществляется через предикат write(L), где L – список. Для удобства обработки списков введены понятия головы и хвоста списка. Голова – первый элемент списка, хвост – остальная часть списка, таким образом хвост списка сам является списком. Для представления списка в виде головы и хвоста используется следующая запись:
Пустой список нельзя разделить на голову и хвост. Рекомендации по работе со списками: 1. Операциями со списками практически всегда используется рекурсия 2. Обычно предикаты для реализации работы со списками имеют несколько клозов. Первый из них относится к простейшему случаю (например, к операции с пустым списком, со списком из одного элемента, с головой списка). Последующие клозы относятся к более общим случаям и имеют следующее назначение: Если список не соответствует простейшему случаю, рассмотренному в первом клозе, то его следует уменьшить на 1 элемент, например, исключить голову, и применить рекурсию к укороченному списку. 3. Предикаты для получения одного списка из другого всегда имеют не менее двух аргументов: первый – исходный список, второй – результат.
Пример
Здесь мы последовательно отрываем голову от списка, и сравниваем ее с искомым числом. Если голова списка совпадает с X то, элемент принадлежит списку, в противном случае мы рекурсивно вызываем предикат prinadl с укороченным на 1 числом элементов списка Сумма элементов списка через 2 аргумента!!! Cписки вводят с клавиатуры Функторы Функторы представляют собой составные типы данных на прологе. Они позволяют структурировать данные для удобства их структурирования и обработки. Функторы соответствуют структурам в языках типа С или записям в Паскале, объявляется в domains следующим образом:
Приведенная программа отыскивает название книги X написанной Дюма, и ценной Z. Функтор Kniga=book(author,title): kniga – тип, book – название. Authr, title – переопределенные типы данных. Аргументами функтора является author и title, однако могут быть и другие функторы в том числе. Одна из наиболее важных задач для которой применяются функторы – объявление предикатов, которые в разных случаях могут принимать значения разных типов. В этом случае необходимо объявить набор функторов, называемых альтернативным доменом.
Если затем указать альтернативный домен в качестве типа аргумента при объявлении предиката (в разделе Predicates), то в качестве аргумента предиката можно будет указывать любой из функторов. Пример
Здесь объявлен альтернативный домен operator и функтор expression, в котором в качестве одного из аргументов указан альтернативный домен. Предикат readterm(тип, имя переменной): тип – альтернативный домен, указанный в разделе domains: имя переменной- переменная с которой связывается функтор. Функтор вводится в точности с его объявлением. Функторы и списки удобно применять для работы с семантическими сетями.
Экспертные системы. Основные механизмы Экспертная система – технология для извлечения решения задачи из базы знаний, представленной в удобном для обработки машиной виде. Имеется два основных механизма экспертных систем: 1. База знаний 2. Машина вывода Соответствует двум составляющим: языку описания задач и алгоритму решения задач. В настоящее время экспертные системы нашли научное применение включает психологию, САПР, промышленное планирование. Задачи, которые решают экспертные системы относится к разделу интеллектуальные. Впервые этот термин ввели Мизец и Фигенбаум. [EB6] Они предложили работать со знаниями как с базой данных, т.е. рассматривать задания как вид данных. Примеры экспертных систем: MYCIN, EMYCIN, Dendrol. Структура экспертной системы представлена на рисунке:
Рис.1 – Структура экспертной системы
Процесс функционирования экспертной системы можно представить следующим образом: 1. Пользователь, желающий получить необходимую информацию через пользовательский интерфейс посылает запрос к экспертной системе 2. Решатель пользуясь базой знаний генерирует и выдает пользователю подходящую информацию, объясняя ход своих рассуждений пользуясь системой объяснений. Пользователь – это специалист предметной области, для которого предназначена система. Обычно его квалификация недостаточно высока, поэтому он нуждается в помощи со стороны экспертной системы. Инженер по знаниям – специалист в области искусственного интеллекта, выступающий в роле промежуточного буфера между экспертом и базой знаний. Также его можно назвать аналитиком. Интерфейс пользователя – комплекс программ, реализующих диалог пользователя с экспертной системой как на стадии ввода информации, так и при получении результата. База знаний (БЗ) – ядро экспертной системы (ЭС), совокупность знаний предметной области, записанная на машинный носитель (на некотором языке, приближенном к естественному). Решатель – программа моделирующая ход рассуждения эксперта на основании знаний, имеющихся в базе знаний. Иначе, это есть дедуктивная машина, машина вывода. Подсистема объяснений – программа, позволяющая получить пользователю ответы на вопросы: «как была получена та или иная рекомендация», «почему система приняла то или иное решение» и т.д. Интеллектуальный редактор базы знаний – программа, предоставляющая инженеру по знаниям возможность создавать базу знаний в диалоговом режиме. Здесь могут быть системы ложных меню, подсказок (help) и другие сервисные средства для работы с базой знаний. Прародители экспертных систем – жрецы, гадалки, дельфийский оракул. Генетическая логика В основе генетических методов лежит теория Дарвина о естественном отборе. В основе генетических алгоритмов лежит простая идея: берут пару наилучших порожденных образцов и порождают их потомка путем взаимного обмена характеристиками (скрещивания crossover). Потомков порождают все время и элитных представителей текущей совокупности. Когда наступает момент и не удается улучшить функционал, производят мутацию, т.е. порождают новые объекты не в результате скрещивания родительских объектов, а путем случайных изменений. Эта процедура ведется до тех пор, пока удается улучшить характеристики функционала. Генетический алгоритм был разработан Джоном Холандом. Пример. Пусть следует максимизировать следующую функцию: F(x,y) = 2x +4y – xy, x+y <= 11, x >=0, y>=0 Сформируем начальную комбинацию
Выберем элиту из 4х наилучших образцов, где функция достигает наибольших значений
Породим из них потомков, например, скрестим 5 и 8 объекты: (2, 5), (0,9)
Т.к. 10 потомок дал больший результат, будем манипулировать им. Скрестим 8 и 10 объекты, получим потомки (2,9) и (0,9). Т.к. нам не удалось улучшить целевую функцию путем скрещивания, перейдем к процессу мутации. Мутация – небольшие произвольные изменения в назначении гена (+/- небольшое значение). Мутация позволяет создавать новый материал, т.к. новые хромосомы перемешиваются с уже существующими. Таким образом мутация позволяет расширить область поиска решений. Осуществим мутацию двух лучших образцов (2,9) и (0, 9) -> (2,10) и (0, 10). (2,10) не удовлетворяет условиям
Возобновляем скрещивание. Процесс завершаем, когда ни мутация, ни скрещивание не улучшают функционал. Недостатки: 1. Проблема преждевременного схождения функции может произойти из-за недостаточного разнообразия хромосом 2. Проблема преждевременного схождения функции может произойти из-за выбора только элитных образцов, которые быстро сокращают свое количество. Сфера применения: 1. Финансы 2. Военная сфера 3. Бизнес Задача коммивояжёра Рассмотрим алгоритм Нильсона на примере зада коммивояжера (или же «бродячего торговца»). Пусть имеется n городов, соединенных дорогами
Введем матрицу затрат C[Cij]
В задаче требуется найти цикл с минимальной суммой затрат из образующих его дуг, которые проходят каждую вершину не более одного раза, за исключением вершины из которой цикл начинается и в которой заканчивается. Для данного метода эвристического поиска применяется способ оценки H(n) предложенный Литтлом, Мерти, Суини. Для этого способа нужно на текущей матрице расстояний сначала найти минимальный элемент в каждой строке, затем найденные элементы вычитают из соответствующих элементов строки.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 178; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

 ) – тавтология.
) – тавтология. , f2 = b->
, f2 = b->  f, f3 = cv
f, f3 = cv 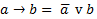

 В итоге получили ситуацию FALSE-> FALSE, следовательно, выводимость имеет место.
В итоге получили ситуацию FALSE-> FALSE, следовательно, выводимость имеет место.