
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Фигура Земли и система координатСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
#1.1. Понятие о фигуре Земли. Уровенные поверхности
Уровенной называют такую поверхность, которая в каждой своей точке перпендикулярна к направлению отвесной линии и имеет постоянный потенциал Fтяж. Уровенных поверхностей может быть сколько угодно. В общем случае уровенные поверхности не параллельны друг другу. Уровенная поверхность никогда не пересекается. Каждая уровенная поверхность образует замкнутую фигуру без разрывов и складок, которая имеет на столько сложную конфигурацию, что математически не выражается. Основная (средняя) уровенная поверхность – поверхность совпадающая со средней поверхностью мирового океана. Геоид – образованная основной уровенной поверхностью замкнутая фигура принимаемая за обобщенную поверхность Земли. Для точного определения поверхности геоида какой-либо точки необходимо выполнить комплекс измерений, непосредственно на поверхности геоида. Что практически не возможно, либо в соответствующей точке на физической поверхности Земли с учетом распределения масс в этом месте, что также не предоставляется возможным. По этой причине было предложено вместо поверхности геоида использовать квазигеоид, – поверхность близкая к поверхности геоида, определяемая только по результатам измерений на земной поверхности без привлечения данных по распределению масс. Максимальное отклонение квазигеоида от геоида 4 м, но большинство считает, что 2 м.
#1.2. Общеземной эллипсоид и референц-эллипсоид
Земной эллипсоид – эллипсоид вращавшийся вокруг малой оси. Чтобы на поверхности можно было работать, необходимо знать его основные параметры: a – большая полуось, a = OE b – малая полуось, b = OP α – полярное сжатие, α = (a-b)/a e – эксцентриситет,
Для определения этих параметров выполняются градусные измерения, которые изначально сводились к определению длины дуги меридиана в 10 градус, а в настоящее время превратились в сложный комплекс астрономо-геодезических, гравиметрических и спутниковых измерений с привлечением данных из других смежных наук. Различают общеземной эллипсоид, который наилучшим образом согласуется с поверхностью геоида в целом и референц-эллипсоид, который наилучшим образом согласуется с геоидом на ограниченной части его поверхности. Требования к общеземному эллипсоиду: 1) центр должен совпадать с центром масс Земли 2) Плоскость экватора должна совпадать с плоскостью земного экватора 3) Объем должен быть равен объему геоида 4) Σh2=min 5) ΣU2=min Требования к референц-эллипсоиду: 1) Ось вращения должна быть II оси вращения Земли 2) Плоскость экватора должна быть II плоскости земного экватора 3) Σh2=min, ΣU2=min – для ограниченной территории Объем может быть не равен объему геоида
#1.3. Основные линии и плоскости земного эллипсоида
Нормаль – перпендикуляр к поверхности данной точки (эллипсоида). Все плоскости проходящие через нормаль называются нормальными плоскостями, а сечение ими поверхности эллипсоида – нормальным сечением. Все сечения не являющиеся нормальными называются наклонными сечениями. Нормальная плоскость ┴ плоскости меридиана называется плоскостью 1-го вертикала. 1-вертикал – плоскость перпендикулярная к меридиану Меридиан и 1-вертикал – главные нормальные сечения.
#1.4. Уклонения отвесных линий
(см. рис.)
В общем случае поверхность геоида и поверхность эллипсоида не II между собой. Уклонением отвесной линии называется угол «u» образованный при несовпадении отвесной линии проведенной в точке на земной поверхности ┴-но геоиду с проведенной в этой же точке ┴-но к эллипсоиду нормалью. Уклонением отвесной линии от нормали к общеземному эллипсоиду называется абсолютным, а от нормали к референц-эллипсоиду – относительным. Уклонение отвесных линий «u» в любой точке для практических целей обычно рассматривают не целиком, а в проекции на плоскость меридиана ξ и на плоскость 1-го вертикала η.
#1.5. Системы координат
Координаты – угловые и линейные величины однозначно определяющие положение точки на какой-либо поверхности или в пространстве относительно принятого их счета. На сферической поверхности наиболее удобными являются географические координаты (широта и долгота) отсчитываемые от поверхности экватора и начального меридиана в виде дуг, которым соответствуют центральные углы. Из-за неправильности форм Земли и неравномерности распределения масс в ней географические координаты не подходят для использования в геодезических работах. Поскольку в общем случае отвесная линия в данной точке не совпадает с нормалью, плоскость меридиана проходящая через отвесную линию параллельна оси вращения Земли и не совпадает с плоскостью геодезического меридиана, проходящего через нормаль и ось вращения эллипсоида. В результате этого несовпадения различают астрономическую и геодезическую системы координат. Астрономические координаты точки определяются из непосредственных наблюдений небесных тел, выполненных на этой точке совершенно и независимо от других точек. Астрономической широтой точки называется угол, отсчитываемый от плоскости экватора в плоскости астрономического меридиана до отвесной линии в этой точке, или дуга астрономического меридиана от экватора до точки. Астрономической долготой точки называется двугранный угол, отсчитываемый от плоскости гринвичского астрономического меридиана до плоскости астрономического меридиана данной точки, или дуга экватора между этими меридианами. Астрономическим азимутом направления называется двугранный угол, отсчитываемый от северной части плоскости астрономического меридиана данной точки по часовой стрелке до отвесной плоскости содержащей данное направление. Геодезические координаты точки получаются по средствам передачи их от какого-то исходного пункта через геометрические построения на поверхности эллипсоида. Геодезической широтой β называется угол, отсчитываемый от плоскости экватора в плоскости геодезического меридиана до нормали проведенной точки, или дуга геодезического меридиана от экватора до точки. Геодезической долготой L называется двугранный угол, отсчитываемый до плоскости геодезического меридиана точки от плоскости геодезического меридиана принятого за начальный, или дуга экватора между этими меридианами. Геодезическим азимутом направления называется двугранный угол, отсчитываемый от северной части плоскости геодезического меридиана точки по часовой стрелке до нормальной плоскости содержащей данное направление. Связь геодезических координат с астрономическими осуществляется через составляющие отклонения отвеса в данной точке: βм=jм-ξм Lм=αм-ηмsecjм Δмк=αмк+(Lм-αм)*secjм
#1.6. Основные системы высот
В высшей геодезии три основные системы высот: Ортометрическая высота точки – ее отстояние от поверхности геоида по отвесной линии. Геодезическая высота точки – ее отстояние от поверхности референц-эллипсоида по нормали. Нормальная высота точки – ее отстояние от поверхности квазигеоида по нормали. Работы выполняются только в ортометрических системах высот.
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 505; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.61.197 (0.01 с.) |

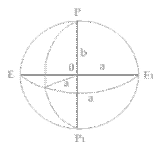 Из-за сложности геоида эта поверхность математически не выражается, поэтому на ней нельзя решать геодезические задачи. Для решения таких задач взамен поверхности геоида принимают поверхность эллипсоида вращения – близкой по форме геоиду, но математически правильной поверхности, на которую можно перенести результаты измерений выполненных на физической поверхности Земли.
Из-за сложности геоида эта поверхность математически не выражается, поэтому на ней нельзя решать геодезические задачи. Для решения таких задач взамен поверхности геоида принимают поверхность эллипсоида вращения – близкой по форме геоиду, но математически правильной поверхности, на которую можно перенести результаты измерений выполненных на физической поверхности Земли.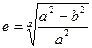

 Высотой точки называется ее отстояние от поверхности принятой за начальную.
Высотой точки называется ее отстояние от поверхности принятой за начальную.


