Результати програмної реалізації мультиплексорів, демультиплексорів, шифраторів, дешифраторів

На рис. 7.4.7 зображено вікно сигнального редактору проекту “shifrator1”.

 

Рис.7.4.7. Результати тестування шифратора 10 на 4

 

На рис. 7.4.8 зображено вікно сигнального редактору проекту “decipherer1”.

 

Рис. 7.4.8. Результати тестування повного 3-розрядного дешифратора з інверсними виходами

 

На рис. 7.4.9 зображено вікно сигнального редактору проекту “multiplexer2”.

 

Рис. 7.4.9. Результати тестування мультиплексора з 2 адресними входами, 4 інформаційними і входом дозволу роботи

 

На рис. 7.4.10 зображено вікно сигнального редактору проекту “demultiplexer1”.

 

Рис. 7.4.10. Результати тестування демультиплексора з 3 адресними входами,1 інформаційним і входом дозволу роботи

Теоретичні відомості про суматори, віднімані

Суматори

Крайній лівий розряд двійкового числа, такого, наприклад, як 101011, називають самим старшим розрядом (ССР), а крайній правий розряд – самим молодшим розрядом (СМР). Нагадаємо, що розряди представленого двійкового числа в порядку зростання старшинства мають ваги (зправа налiво) 1, 2, 4, 8, 16, 32.

Оскільки в двійкових числах присутні лише дві цифри (0 і 1), таблиця додавання досить проста. Вона приведена на рис. 7.5.1. Як і в випадку додавання десяткових чисел, три перших результати не викликають питань. Що стосується останньої задачі (1+1), то при складанні десяткових чисел в даному випадку відповіддю було б число 2. Таким чином, при двійковому додаванні 1+1=0 плюс перенос 1 в сусідній старший двійковий розряд.

 

 

Рис. 7.5.1. Таблиця двійкового додавання

 

Ще один приклад на складання двійкових чисел представлено на рис. 7.5.2,а.

 

а)

б)

Рис. 7.5.2. Двійкове додавання а) – приклад на двійкове додавання; б) - скорочена форма таблиці двійкового додавання

Рішення виглядає простим, доки ми не доходимо до розряду двійок, де треба знайти двійкову суму. В десятковій системі ця сума дорівнює 3, що відповідає числу 11. Цей випадок не відображений на рис. 7.5.1. Сума 1+1+1 може виникнути в будь-якому розряді, за винятком розряду одиниць. В нову (скорочену) таблицю на рис. 7.5.2,б включена ще одна можлива комбінація 1+1+1.

Ця таблиця справедлива для всіх розрядів двійкових чисел, за виключенням розряду одиниць.

У відповідній таблиці дійсності (табл. 7.5.1) надано всі можливі комбінації двійкових однорозрядних доданків А, В і сигналу переносу С_in.

 

Табл.7.5.1. Таблиця дійсності повного суматора

Входи	Виходи
Сin	В	А	S	С0
Перенос + В + А	Сума	Перенос

 

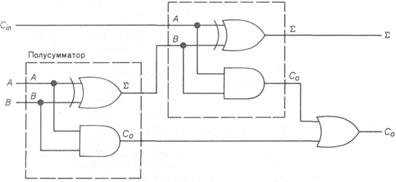
Повні суматори використовуються для складання всіх двійкових розрядів за виключенням одиниць. Вони повинні мати додатковий вхід переносу.

Повний суматор – 3-входова схема. Сигнали на його виходах S і С₀ отримуються внаслідок складання трьох вхідних сигналів (на входах А, В і С_in).

На рис. 7.5.3 показана розгорнута логічна схема повного суматора. Вона основана на структурній схемі з двома напівсуматорами.

Рис.7. 5.3. Логічна схема повного суматора

 

На рис. 7.5.4. приведена інша схема повного суматора з використанням двох логічних елементів виключного АБО і трьох логічних елементів І-НЕ. Зазначимо, що схеми, приведені на рис. 7.5.3. і 7.5.4. відрізняються лише заміною логічних елементів І та АБО на логічні елементи І-НЕ.

Рис. 7.5.4. Логічна схема повного суматора з використанням виключного АБО та І-НЕ

 

Напівсуматори і суматори зазвичай використовують разом. Велика кількість схем, аналогічних до напівсуматорів і повних суматорів, є в складі мікропроцесорних арифметично-логічних приладів (АЛП). Мікропроцесорні АЛП можуть виконувати і операції віднімання, при цьому використовуються ті ж самі напівсуматори і суматори.

Певним чином поєднуючи між собою напівсуматори та повні суматори отримують пристрої, що одночасно виконують додавання декількох двійкових розрядів. Пристрій, схема якого показана на рис. 7.5.5. виконує операцію додавання двох 3-розрядних чисел. Числа-доданки А₂А₁А₀ і В₂В₁В₀. Сигнали, що відповідають значенням розряду одиниць в доданках, поступають на вхід суматора розряду одиниць (напівсуматора). Вхідними сигналами для повного суматора розряду двійок є сигнал переноса з виходу напівсуматора (подається на вхід С_in) і значення А₁ і В₁ розряду двійок і доданків. Далі суматор четвірок складає А₂ і В₂ і сигнал переносу з суматора двійок. На двійковому виході пристрою (показано в правому нижньому куті рис. 7.5.5) встановлюється двійкова сума.

В результаті додавання двох 3-розрядних двійкових чисел можливо отримати 4-розрядне число, тому на індикаторі суми маємо додатковий розряд вісімок. Зверніть увагу, що даний розряд пов’язаний з виходом (С₀) суматора четвірок.

 

Рис. 7.5.5. 3-розрядний паралельний суматор

 

Логіка роботи розглядуваного 3-розрядного суматора майже не відрізняється від послідовності операцій, що виконуються при додаванні вручну (додаванні однорозрядних чисел плюс перенос в наступний розряд). Однак електронний суматор виконує дані операції набагато швидше.

Ще раз зазначимо, що в багаторозрядних суматорах напівсуматори використовуються лише для додавання в розряді одиниць; у всіх iнших розрядах використовуються повні суматори. Описаний вище 3-розрядний суматор називається паралельним суматором.

В паралельному суматорі інформаційні біти всіх розрядів поступають на входи одночасно. Результат (сума) з’являється на виході практично миттєво. Паралельний суматор на рис. 7.5.5 відноситься до класу комбінаційних логічних схем. Для фіксації даних на входах і виходах суматорів зазвичай використовують різноманітні додаткові регістри.

 

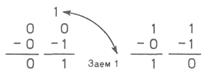
Віднімачі

Далі буде показано, що суматори і віднімачі подібні один до одного, і, крім того напіввіднімачі та повні віднімачі використовуються аналогічно напівсуматорам та повним суматорам. Таблиця двійкового віднімання приведена нижче, в ній наведено правила віднімання двійкових чисел, що подані на рис. 7.5.6, у вигляді таблиці дійсності. Ми бачимо, що В віднімається з А (А і В – вхідні сигнали), результат (різниця) появляється на виході D₁. Якщо В більше за А (як в рядку 2 таблиці), потрібно позичити 1 в сусіднього старшого розряду. Сигнал позики вказано у стовпці В₀.

 

Табл. 7.5.2. Таблиця двійкового віднімання

Входи	Виходи
А	В	Di	B0
A-B	Різниця	Позика

 

Рис. 7.5.6. Таблиця двійкового віднімання

 

При відніманні багаторозрядних двійкових чисел треба приймати до уваги позику “одиниць” в більш старших розрядах.

Таблиця дійсності, що містить всі можливі комбінації, які виникають при відніманні двійкових чисел, приведена нижче.

Табл. 7.5.3. Таблиця дійсності повного віднімача

Входи	Виходи
A	В	Bin	Di	B0
A – B – Bin	Різниця	Позика

 

Умовне позначення повного віднімача показано на рис. 7.5.7,а. Ліворуч – входи А, В, B_in, праворуч – виходи D_i, B₀.По аналогії з повним суматором повний віднімач можливо зібрати з двох напіввіднімачів і логічного елемента АБО. На рис. 7.5.7,б показано як потрібно поєднати напіввіднімачі і логічний елемент АБО, щоб отримати повний віднімач. Розгорнута логічна схема повного віднімача наведена на рис. 7.5.7,в. Ця схема працює у відповідності до таблиці дійсності 7.5.3. При необхідності логічні елементи І та АБО можливо замінити на три логічних елемента І-НЕ. В цьому випадку ми отримаємо схему повного віднімача, аналогічну до схеми повного суматора.

 

в)

б)

а)

Рис. 7.5.7. Повний віднімач а) – умовне графічне позначення; б) – структурна схема для випадку використання двох напіввіднімачів і логічного елемента АБО; в) – принципова схема

 

Поєднуючи між собою напіввіднімачі і повні віднімачі, отримують пристрої, що називають паралельними віднімачами. Аналогічним чином до розглядуваного вище трьохрозрядного суматора збирається і паралельний віднімач. Суматор на рис. 7.5.5 називається паралельним, оскільки інформаційні біти всіх розрядів в доданках поступають на даний суматор одночасно.

На рис. 7.5.8 подано структурну схема, отримана шляхом об’єднання одного напіввіднімача і трьох повних віднімачей. Це схема 4-розрядного паралельного віднімача, який виконує операцію віднімання одного двійкового числа B₃B₂B₁B₀ з двійкового числа А₃А₂А₁А₀. Зверніть увагу, що верхній (на схемі) віднімач виконує віднімання в розряді одиниць (СМР). Вихід B₀ цього віднімача пов’язаний з віднімачем розряду двійок.

 

Рис. 7.5.8. 4-розрядний паралельний віднімач

 

Взагалі вихід позики B₀ кожного віднімача пов’язаний з входом позики B_in віднімача сусіднього старшого розряду. Ці лінії зв’язку “слідкують” за позиками в процесі віднімання двійкових чисел.

 

7.5.3 Програми реалізації суматорів, віднімачів в інтегрованому середовищі MAX+PLUS II

Програма для реалізації 4-розрядного суматора за допомогою мови AHDL в інтегрованому середовищі MAX+PLUS II має наступний вигляд:

SUBDESIGN add_gate

(

A[4..1], B[4..1], cin: input;

C[4..1], cout: output;

)

VARIABLE

carry_out[5..1]: node;

BEGIN

carry_out[1] = cin;

FOR i IN 1 TO 4 GENERATE

C[i] = A[i] $ B[i] $ carry_out[i];

carry_out[i + 1] = CARRY (A[i] & B[i] # carry_out[i] & (A[i] # B[i]));

END GENERATE;

cout = carry_out[5];

END;

Програма для реалізації 4-розрядного віднімача за допомогою мови AHDL в інтегрованому середовищі MAX+PLUS II має наступний вигляд:

SUBDESIGN add_sub

(

A[4..1], B[4..1]: input = GND;

Res[4..1], Cout: output;

)

VARIABLE

S[4..1]: node;

Cout_int: node;

BEGIN

(Cout_int, S[]) = (GND, A[]) - (GND, B[]);

(Cout, Res[]) = (Cout_int, S[]);

END;