ТЕМА 2 «Прямые и точки, принадлежащие плоскости»

 

Задачи по теме 2 выдаются на второй неделе, после проведения практического занятия 2, с учетом знаний, полученных на лекции 1 [1, 2, 3, 4, 5].

Для решения задач необходимо усвоить следующий теоретический материал:

а) частное и общее положение прямых;

б) частное и общее положение плоскостей;

в) условия принадлежности точки и прямой плоскости;

г) условия параллельности прямой и плоскости.

2.1 Теория к выполнению индивидуального задания по теме «Принадлежность прямой и точки плоскости»

 

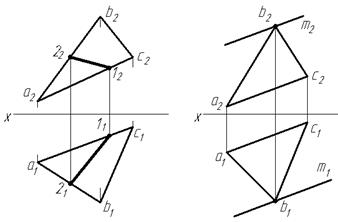
Из элементарной геометрии известно, что прямая принадлежит плоскости, если она:

а) проходит через две точки, принадлежащие данной плоскости;

б) проходит через точку, принадлежащую данной плоскости, и параллельна какой-либо прямой, находящейся в этой плоскости или ей параллельной.

На рисунке 5 построены произвольные прямые, принадлежащие плоскости ΔАВС. На рисунке 5а прямая 1-2 удовлетворяет первому условию, а на рисунке 5б прямая m удовлетворяет второму условию (точки 1 и 2 лежат на сторонах треугольника, т.е. заведомо принадлежат ему, а прямая m параллельна стороне АС и проходит через точку В треугольника).

 

а б

Рисунок 5 ‑ Построение прямых, принадлежащих плоскости

Прямые особого положения в плоскости. К прямым особого положения в плоскости относятся прямые уровня (горизонтали, фронтали, профильные прямые) и линии ската.

Горизонтали плоскости ‑ это прямые, лежащие в данной плоскости и параллельные плоскости проекций Н.

Горизонтальная проекция горизонтали всегда параллельна горизонтальному следу плоскости, а фронтальная ‑ параллельна оси X.

На рисунке 6 изображены горизонтали плоскостей, заданных:

а) следами;

б) параллельными прямыми;

в) треугольником.

а б в

Рисунок 6 ‑ Построение горизонталей в плоскостях общего положения

 

Фронтали плоскости ‑ это прямые, лежащие в заданной плоскости и параллельные плоскости проекций V.

Фронтальная проекция фронтали всегда параллельна фронтальному следу плоскости, а горизонтальная параллельна оси X (рисунок 7а).

На рисунке 7б изображена фронталь плоскости, заданной Δ ABC, которая проходит через точки М, N (m₁, m₂ и n₁, n₂ – на эпюре).

На рисунке 7в фронталь плоскости, заданной параллельными прямыми (АС // MN), проходит через точку А.

а б в

Рисунок 7 ‑ Построение фронталей в плоскостях общего положения

 

Точка принадлежит плоскости, если лежит на прямой, принадлежащей плоскости. Рассмотрим подробнее на примере.

Задача. Постройте произвольный пятиугольник abcde, все точки которого лежат в одной плоскости (рисунок 8).

Решение: Точки abc на фронтальной и горизонтальной плоскостях проекций строим по координатам (соблюдая перпендикулярность линий связи оси Х). Три точки однозначно задают положение плоскости в пространстве. Чтобы четвертая точка легла в плоскость, ее следует обязательно к плоскости привязать. Для построения точки d проводим произвольную прямую а-1, которая заведомо принадлежит плоскости треугольника. На ее продолжении произвольно отмечаем точку (т.е. две проекции точки). Для построения точки е произвольно проводим прямую с-2; на ее продолжении отмечаем точку с (т.е. две проекции точки с₁ и с₂).

 

Рисунок 8 ‑ Построение пятиугольника

2.2 Пример оформления задач 2.1 и 2.2

 

Для выполнения задачи 2.1 постройте горизонтали и фронтали для трех плоскостей: треугольник АВС задан координатами, две другие плоскости смотрите в индивидуальных заданиях (рисунок 9).

 

 

Рисунок 9 ‑ Пример оформления задач 2.1 и 2.2