
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проаналізувати класифікацію об'єктів дослідженняСодержание книги
Поиск на нашем сайте
Объекты исследования характеризуются свойствами: степень сложности, полнота оприорной информации, воспроизводимость и управляемость. Сложность объекта – число состояний которые в соответствии с целью исследования и техникой эксперимента можно различить. Под оприорной информацией понимается информация, которая известна до начала моделирования. Если об объекте известно всё, то исследование не имеет смысла. Управляемость – если объекты управляемые, то исследователь может изменять любые исходные величины данного объекта. В частично-управляемых можно ставить эксперимент, а за неуправляемыми возможно только наблюдать. Воспроизводимость – это свойство объекта возвращаться в прежнее состояние.
4. Охарактеризувати основні принципи моделювання функціональних залежностей при обробці даних. Визначення констант функції y = f (xi, a, b) на основі методу найменших квадратів Анализ различных технологических процессов требует разработку эмпирических формул. Рассмотрим две величины х и у, х - как зависимую и у - как независимую величину, между ними однозначное соответствие. В общем случае задачу сформулируем таким образом: Значениям х1; х2; х3…хn поставим в соответствие у1; у2; у3…уn требуется подобрать вид аналитической зависимости у=f(x) связывающей переменные х и у – такая зависимость называется эмпирической, их получают путём выбора эмпирической формулы, а за тем определением коэффициентов выбранной формулы. Рассмотрим функцию:
на следующем этапе записываем выражение для функционала F(a,b)
где: уі - ордината экспериментальной і-той точки; f(x,a,b) – расчётная величина. Метод наименьших квадратов утверждает, что «наилучшей» кривой будет такая, для которой сумма квадратов отклонений экспериментальных значений уі от значений функции f(x,a,b) минимальна. Другими словами в этом уравнении необходимо найти такие а и b при которых разницы значений расчётных от экспериментальных при возведении в квадрат этих разниц, после суммирования, давали наименьшее значение. Для этого на следующем этапе находим частные производные dF/da и dF/db, которые затем приравниваем к нулю, и при данном условии решаем полученную систему уравнений, что даст наилучшие значения числовых параметров а и b.
5. Розкрити сутність методу найменших квадратів. Визначення константи, що входить в рівняння y = ax на основі методу найменших квадратів
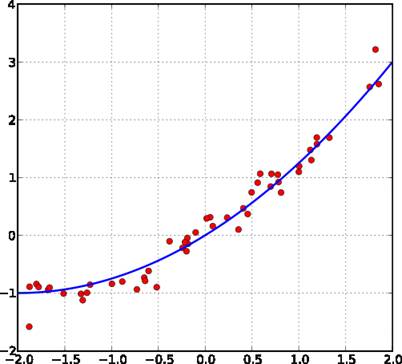
Пример кривой, проведённой через точки, имеющие нормально распределённое отклонение от истинного значения.
Метод наименьших квадратов основан на утверждении, что наилучшими значениями констант уравнения регрессии будут те, для которых сумма квадратов отклонений между расчётными и экспериментальными значениями минимальна
Для нахождения констант входящих в уравнение, необходимо найти частные производные по каждой из констант, приравнять их к нулю и решить систему полученных уравнений относительно каждой константы. Алгоритм нахождения констант, входящих в уравнение y=ax: F= Берем частную производную по da: Находим а:
6. Визначення констант, що входить в рівняння y = ax + b на основі методу найменших квадратів
Метод наименьших квадратов основан на утверждении, что наилучшими значениями констант уравнения регрессии будут те, для которых сумма квадратов отклонений между расчётными и экспериментальными значениями минимальна
Для нахождения констант входящих в уравнение, необходимо найти частные производные по каждой из констант, приравнять их к нулю и решить систему полученных уравнений относительно каждой константы. Алгоритм нахождения констант, входящих в уравнение y=ax + b:
F=
Берем частную производную по da Берем частную производную по db
Результаты дифференцирования:
Выразим xiyi Выразим yi
Для нахождения констант a и b необходимо решить систему:
7. Розкрити сутність моделювання напруження течії металу s на основі методу термомеханічних коефіцієнтів. Принципи побудови графічних залеж-ностей для термомеханічних коефіцієнтів σ прямо пропорционально зависит от степени и скорости деформации (т.к. чем они выше тем более выражено наблюдается явление упрочнения) и обратно пропорционально температуре деформации (т.к. чем больше температура тем меньше усилия необходимо приложить для начала пластической деформации). Профессор Зюзин предложил следующую зависимость для определения напряжения течения металла
, где
kε=σε/σ0 Kε=A1εn1 ku=σu/σ0 Ku=A2un2 kТ=σТ/σ0 KТ=A3e(-n3*T)
σε - значение напряжения течения металла при заданном текущем σu - значение напряжения течения металла при заданном текущем U и фиксированных базових значениях σT - значение напряжения течения металла при заданном текущем T и фиксированных базових значениях Темомеханические коэффициенты находятся на основе имеющейся пластометрической экспериментальной информации. Алгоритм нахождения kε Назначается диапазон изменения фиксированных базовых значениях U и T. Далее, при помощи метода наименьших квадратов находятся константы A1,n1
8. Раскрыть сущность метода получения формулы Профессор В.И. Зюзин предложил следующую зависимость:
где σ0 - базисное значение напряжения течения металла, установленное при степени деформации ε=0,1, скорости деформации и =10 с-1 и температуре Т=1000 0С;
Для нахождения термомеханических коэффициентов были построены графики. При и =10 с-1 и Т=1000 0С
Коэффициенты А2, т2 находим по методу наименьших квадратов. Согласно методу, наилучшими параметрами будут те, для которых сумма квадратов отклонений будет минимальна. График ku строится аналогично при ε=0,1 и Т=1000 0С. При ε=0,1 и и =10 с-1
Точки аппроксимируются по формуле
9. Раскрыть сущность моделирования течения металла Напряжение течения металла зависит от марки стали, скорости и степени деформации. Это значит, что у нас 3 фактора: Для начала необходимо определить кодовые значения факторов и соответствующие им натуральные значения. Например:
Где б- шаг варьирования. Связь между натуральными значениями и кодовыми определяют по формуле:
где Хі – натуральное значение фактора; Хі0 – натуральное значение фактора на среднем уровне; хі – кодовое значение фактора. После проведения всех 15 опытов, получим план-матрицу эксперимента:
При помощи программы Statistica, которая основана на методе наименьших квадратов (т.е. сумма квадратов отклонений расчётных точек от исходных точек должна быть минимальной), получим коэффициенты, входящие в уравнение расчёта напряжения течения металла по формуле профессора В.И Зюзина: А, п1, п2, п3. Подставим их в уравнение и получим окончательную формулу для расчета
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.175.48 (0.008 с.) |


 ,
,


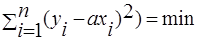
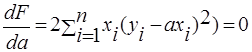










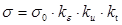
 -базисное значение напряжения течения металла, при
-базисное значение напряжения течения металла, при 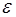 =0.1,
=0.1,  = 10с-1, T= 1000 С
= 10с-1, T= 1000 С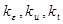 -термомеханические коэффициенты
-термомеханические коэффициенты




 . Раскрыть сущность метода расчета констант в данной формуле.
. Раскрыть сущность метода расчета констант в данной формуле. ,
, - термомеханические коэффициенты.
- термомеханические коэффициенты. kε в точках определены по формуле
kε в точках определены по формуле 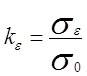 на основе экспериментальной информации. Эти точки аппроксимируются уравнением:
на основе экспериментальной информации. Эти точки аппроксимируются уравнением:  .
. kT в точках определены по формуле
kT в точках определены по формуле

 , где
, где 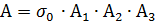
 на основе метода планируемого эксперимента.
на основе метода планируемого эксперимента. Известны также пределы изменения этих факторов. Планирование на основе многофакторного эксперимента позволяет уменьшить число опытов и повысить точность коэффициентов получаемых уравнений регрессии. Для трехфакторного эксперимента число опытов равно 15, а звездное плечо равно 1,215.
Известны также пределы изменения этих факторов. Планирование на основе многофакторного эксперимента позволяет уменьшить число опытов и повысить точность коэффициентов получаемых уравнений регрессии. Для трехфакторного эксперимента число опытов равно 15, а звездное плечо равно 1,215.






