Асимметричные алгоритмы шифрования.

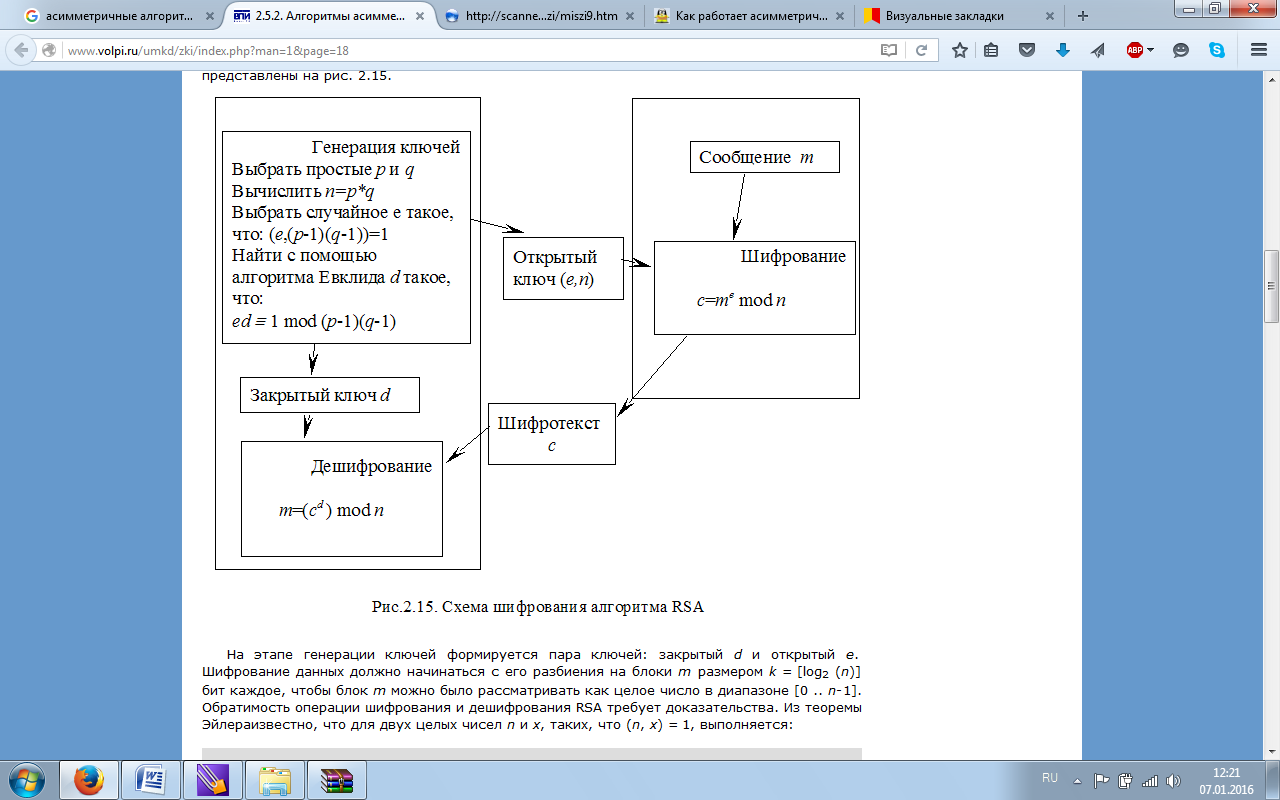
Ассиметричные системы также называют криптосистемами с открытым ключом (RSA, El-Gamal).Это такой способ шифрования данных, при котором открытый ключ передается по открытому каналу (не скрывается) и используется для проверки электронной подписи и для шифрования данных. Для дешифровки же и создания электронной подписи используется второй ключ, секретный.

При использовании криптосистем с открытым ключом стороны не обязаны встречаться, знать друг друга и иметь секретные каналы связи. Это преимущество становится еще более актуальным в случае большого количества пользователей системы. Тогда, к примеру, один пользователь может «закрыто» связаться с другим, взяв некоторую информацию (открытый ключ) из общедоступной базы данных (банка ключей).

Различие ключей (открытого и личного) в криптографии с открытыми ключами позволило создать следующие технологии: электронные цифровые подписи, распределенная проверка подлинности, согласование общего секретного ключа сессии, шифрование больших объемов данных без предварительного обмена общим секретным ключом.

Алгоpитмы кpиптосистемы с откpытым ключом м ожно использовать в тpех назначениях:

- Как самостоятельные сpедства защиты пеpедаваемых и хpанимых данных.

- Как сpедства для pаспpеделения ключей. Алгоpитмы - более тpудоемки, чем тpадиционные кpиптосистемы. Поэтому часто на пpактике pационально с помощью систем с открытым ключом pаспpеделять ключи, объем котоpых как инфоpмации незначителен. А потом с помощью обычных алгоpитмов осуществлять обмен большими инфоpмационными потоками.

- Сpедства аутентификации пользователей (электронная цифровая подпись).

Алгоритм RSA

(Выбираются два простых (!) числа p и q

Вычисляется их произведение n(=p*q)

Выбирается произвольное число e (e<n), такое, что НОД(e,(p-1)(q-1))=1, то есть e должно быть взаимно простым с числом (p-1)(q-1).

Методом Евклида решается в целых числах (!) уравнение e*d+(p-1)(q-1)*y=1. Здесь неизвестными являются переменные d и y – метод Евклида как раз и находит множество пар (d,y), каждая из которых является решением уравнения в целых числах.

Два числа (e,n) – публикуются как открытый ключ.

Число d хранится в строжайшем секрете – это и есть закрытый ключ, который позволит читать все послания, зашифрованные с помощью пары чисел (e,n).

 

Как же производится собственно шифрование с помощью этих чисел:

Отправитель разбивает свое сообщение на блоки, равные k=[log2(n)] бит, где квадратные скобки обозначают взятие целой части от дробного числа.

Подобный блок, как Вы знаете, может быть интерпретирован как число из диапазона (0;2k-1). Для каждого такого числа (назовем его mi) вычисляется выражение ci=((mi)e)mod n. Блоки ci и есть зашифрованное сообщение Их можно спокойно передавать по открытому каналу, поскольку.операция возведения в степень по модулю простого числа, является необратимой математической задачей. Обратная ей задача носит название "логарифмирование в конечном поле" и является на несколько порядков более сложной задачей. То есть даже если злоумышленник знает числа e и n, то по ci прочесть исходные сообщения mi он не может никак, кроме как полным перебором mi.

А вот на приемной стороне процесс дешифрования все же возможен, и поможет нам в этом хранимое в секрете число d. Достаточно давно была доказана теорема Эйлера, частный случай которой утвержает, что если число n представимо в виде двух простых чисел p и q, то для любого x имеет место равенство (x(p-1)(q-1))mod n = 1. Для дешифрования RSA-сообщений воспользуемся этой формулой. Возведем обе ее части в степень (-y): (x(-y)(p-1)(q-1))mod n = 1(-y) = 1. Теперь умножим обе ее части на x: (x(-y)(p-1)(q-1)+1)mod n = 1*x = x.

А теперь вспомним как мы создавали открытый и закрытый ключи. Мы подбирали с помощью алгоритма Евклида d такое, что e*d+(p-1)(q-1)*y=1, то есть e*d=(-y)(p-1)(q-1)+1. А следовательно в последнем выражении предыдущего абзаца мы можем заменить показатель степени на число (e*d). Получаем (xe*d)mod n = x. То есть для того чтобы прочесть сообщение ci=((mi)e)mod n достаточно возвести его в степень d по модулю m: ((ci)d)mod n = ((mi)e*d)mod n = mi.)

На самом деле операции возведения в степень больших чисел достаточно трудоемки для современных процессоров, даже если они производятся по оптимизированным по времени алгоритмам. Поэтому обычно весь текст сообщения кодируется обычным блочным шифром (намного более быстрым), но с использованием ключа сеанса, а вот сам ключ сеанса шифруется как раз асимметричным алгоритмом с помощью открытого ключа получателя и помещается в начало файла.