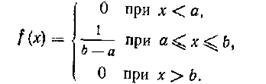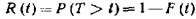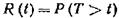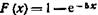Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие снв, функция ее распределенияСтр 1 из 4Следующая ⇒ Тема 6. Случайные непрерывные величины (СНВ) План: 1. Понятие СНВ, функция ее распределения 2. Понятие плотности распределения, функция плотности НСВ 3. Числовые характеристики НСВ. 4. Законы распределения НСВ. 5. Центральная предельная теорема (теорема Ляпунова). Теоретические сведения Понятие СНВ, функция ее распределения Случайной непрерывной величиной являетсявеличина, которая может принять любое из значений некоторого промежутка. Здесь нельзя отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины. Случайная непрерывная величина, принимать все свои значения из некоторого конечного или бесконечного промежутка. Число возможных значений случайной дискретной величины может быть конечным или бесконечным. При рассмотрении ДСВ рассматривалась функция F(x) распределения случайной дискретной величины. Аналогично можно вест речь и о функции распределения случайной непрерывной величины, для определенности ее так же обозначают как F(x). Вместо термина " функция распределения " используют термин " интегральная функция ", смысл которого будет понятен в дальнейшем..
Свойства функции распределения случайной непрерывной величины аналогичны свойствам функция распределения случайной дискретной величины. Они были приведены при рассмотрении случайных дискретных величин. Функция F(x) не убывающая, непрерывная, множество значений промежуток [0; 1]. Случайной непрерывной величиной является величина, функция распределения F(x) которой, непрерывна на всей числовой оси. Функция распределения СНВ F(x) есть кусочно-дифференцируемая функция с непрерывной производной. Вероятность того, что случайная величина примет значение, заключенное в некотором интервале (а, b), равна приращению функции распределения на этом интервале; P(a ≤ X ≤b) = F (b) - F (а). При рассмотрении функции распределения, числовой промежуток записывается так же в виде [x1; x2], тогда вероятность того, что случайная величина примет значение, заключенное в этом интервале равна: p(x1≤ x ≤ x2) = F (x2) - F (x1).- что более понятно и привычно. Вероятность того, что случайная непрерывная величина X примет одно определенное значение, равна нулю.
Задание 6-1. Случайные непрерывные величины заданы функциями распределения 1. Найти вероятности того, что в результате испытания величина X примет значение, принадлежащее интервалу (0;2) Решение. P(0<x<2)=F(2)-F(0)=(2/4+1/4)-(0/4+1/4)=1/2 2. Начертить график данной функции распределения. Задание 6-2. 1. Задана плотность вероятности случайной величины Х.

Решение. Искомая вероятность Р (0,5 < X < 1)= 2. Задана плотность вероятности случайной величины X
Найти вероятность того, что в результате испытания X примет значение, принадлежащее интервалу (0,5; 1). Решение. Искомая вероятность равна
3. Выполнить задания [1[1], С 64-78] 1). Пример 2 с 65 3). № 365 с 68 5). № 372 – 376 с 75 2). Пример 4 с 66 4). Пример 4 с 71
Задание 6-3. 1. Случайная величина X задана плотностью распределения
Задание 6-4. [5[2], C 126], примеры 1-2. Законы распределения НСВ 5.1. Равномерное распределение. Распределение вероятностей непрерывной случайной величины X, принимающей все свои значения из отрезка [а; 6], называется равномерным, если ее плотность вероятности на этом отрезке постоянна, а вне его равна нулю, т. е.
Но, как известно Итак, плотность вероятности непрерывной случайной величины X, распределенной равномерно на отрезке [а; 6], имеет вид:
Задание 6-5. На отрезке [а; b]наугад указывают точку. Какова вероятность того, что эта точка окажется в левой половине отрезка? Обозначим через X случайную величину,— координата выбранной точки. X распределена равномерно (в этом и состоит точный смысл слов: «наугад указывают точку»), а так как середина отрезка [а; 6] имеет координату ^i—, то искомая вероятность равна (см. § 49, п. 2):
Впрочем, этот результат был ясен с самого начала.
Функция надежности Будем называть элементом некоторое устройство независимо от того, "простое" оно или "сложное". Пусть элемент начинает работать в момент времени t0=0, а по истечении времени длительностью t происходит отказ. Обозначим через Т непрерывную случайную величину - длительность времени безотказной работы элемента. Если элемент проработал безотказно (до наступления отказа) время, меньшее t то, следовательно, за время длительностью t наступит отказ. Таким образом, функция распределения F (t)=P(T<t) определяет вероятность отказа за время длительностью t. Следовательно, вероятность безотказной работы за это же время длительностью t, т. е. вероятность противоположного события Т > t, равна
Функцией надежности R (t) называют функцию, определяющую надежность работы элемента за время длительностью t:
Задание 6-12. 1. Написать функцию распределения F (х) и плотность вероятности f (х) непрерывной случайной величины X, распределенной по показательному закону с l = 5.
2. Непрерывная случайная величина X распределена по показательному закону:
Найти вероятность того, что в результате испытания X попадет в интервал (0.4. 1).
4. Непрерывная случайная величина X распределена по показательному закону
Найти математическое ожидание, среднее к в ад и этическое отклонение и дисперсию л.
5 Время безотказной работы элемента распределено по показательному закону
где t — время, ч. Найти вероятность того, что элемент проработает безотказно 100 ч. Ответ. 0,37. Контрольные вопросы и задания 1. Определение СНВ 2. Понятие интегральной и дифференциальной функции, их свойства и график 3. Формулы для нахождения М(Х) и D(X). 4. Алгоритм нахождения среднего квадратичного отклонения для СНВ 5. Дать характеристику законам распределения СНВ. 6. Понятие функции надежности. Примерная тематика практических замятий 1. Вычисление вероятностей и нахождения характеристик для НСВ с помощью функции плотности и интегральной функции распределения. 2. Решение задач на формулу геометрического определения вероятности (для одномерного случая, для двумерного случая, для простейших функций от двух независимых равномерно распределенных величии) 3. Вычисление вероятностей для нормально распределенной величины (или суммы нескольких нормально распределенных величин); 4. Вычисление вероятностей и нахождение характеристик для показательно распределенной величины Требования к знаниям умениям и навыкам Студент должен знать определение и свойства функции плотности НСВ; формулу функции плотности для равномерно распределённой НСВ; определение и свойства интегральной функции распределения НСВ. Уметь вести расчет вероятностей для НСВ по её функции плотности и интегральной функции распределения. Вычислять математическое ожидания, дисперсию, среднеквадратическое отклонение. и медиану НСВ.
1. Андрюхаев Х.М. Сборник задач по теории вероятностей. М. Просвещение. 1985.
[2] Гмурман. В.Е. Теория вероятностей и математическая статистика. М. Высшая школа. 2000. Тема 6. Случайные непрерывные величины (СНВ) План: 1. Понятие СНВ, функция ее распределения 2. Понятие плотности распределения, функция плотности НСВ 3. Числовые характеристики НСВ. 4. Законы распределения НСВ. 5. Центральная предельная теорема (теорема Ляпунова). Теоретические сведения Понятие СНВ, функция ее распределения Случайной непрерывной величиной являетсявеличина, которая может принять любое из значений некоторого промежутка. Здесь нельзя отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины. Случайная непрерывная величина, принимать все свои значения из некоторого конечного или бесконечного промежутка. Число возможных значений случайной дискретной величины может быть конечным или бесконечным. При рассмотрении ДСВ рассматривалась функция F(x) распределения случайной дискретной величины. Аналогично можно вест речь и о функции распределения случайной непрерывной величины, для определенности ее так же обозначают как F(x). Вместо термина " функция распределения " используют термин " интегральная функция ", смысл которого будет понятен в дальнейшем..
Свойства функции распределения случайной непрерывной величины аналогичны свойствам функция распределения случайной дискретной величины. Они были приведены при рассмотрении случайных дискретных величин. Функция F(x) не убывающая, непрерывная, множество значений промежуток [0; 1]. Случайной непрерывной величиной является величина, функция распределения F(x) которой, непрерывна на всей числовой оси. Функция распределения СНВ F(x) есть кусочно-дифференцируемая функция с непрерывной производной. Вероятность того, что случайная величина примет значение, заключенное в некотором интервале (а, b), равна приращению функции распределения на этом интервале; P(a ≤ X ≤b) = F (b) - F (а). При рассмотрении функции распределения, числовой промежуток записывается так же в виде [x1; x2], тогда вероятность того, что случайная величина примет значение, заключенное в этом интервале равна: p(x1≤ x ≤ x2) = F (x2) - F (x1).- что более понятно и привычно. Вероятность того, что случайная непрерывная величина X примет одно определенное значение, равна нулю.
Задание 6-1. Случайные непрерывные величины заданы функциями распределения 1. Найти вероятности того, что в результате испытания величина X примет значение, принадлежащее интервалу (0;2) Решение. P(0<x<2)=F(2)-F(0)=(2/4+1/4)-(0/4+1/4)=1/2 2. Начертить график данной функции распределения.
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.252.140 (0.003 с.) |


 =x2÷10,5=12-0,52= 1-0,25 = 0,75.
=x2÷10,5=12-0,52= 1-0,25 = 0,75.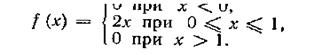


 Определить математическое ожидание, дисперсию и среднее квадратическое отклонение величины X. Согласно определениям 1 и 2 имеем:
Определить математическое ожидание, дисперсию и среднее квадратическое отклонение величины X. Согласно определениям 1 и 2 имеем:


 » 0,47.
» 0,47.
 Отсюда получим
Отсюда получим =1, то из последнего равенства получим c=1/(b-a)
=1, то из последнего равенства получим c=1/(b-a)