Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон равномерного распределения вероятностей
При решении задач, которые выдвигает практика, приходится сталкиваться с различными распределениями непрерывных случайных величин. Плотности распределений непрерывных случайных величин называют также законами распределений. Часто встречаются, например, законы равномерного, нормального и показательного распределений. В настоящем параграфе рассматривается закон равномерного распределения вероятностей. Нормальному и показательному законам посвящены последующие темы. Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение. Приведем пример равномерно распределенной непрерывной случайной величины. Пример. Шкала измерительного прибора проградуирована в некоторых единицах. Ошибку при округлении отсчета до ближайшего целого деления можно рассматривать как случайную величину X, которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Таким образом, X имеет равномерное распределение. 3. Числовые характеристики НСВ. 1. Математическим ожиданием непрерывной случайной величины- X, возможные значения которой принадлежат отрезку [а, b], называют определенный интеграл М(Х) = Если возможные значения принадлежат всей оси Ох, то М(Х) = Предполагается, что несобственный интеграл сходится абсолютно, т, е. существует интеграл то М(Х) = По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины. 2. Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения. Если возможные значения X принадлежат отрезку [а, b],то D(x)= Если возможные значения принадлежат всей оси Ох, то D(x)=
3. Среднееквадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством Можно доказать, что свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.
Легко получить для вычисления дисперсии более удобные формулы: D(x)= Задание 6-3. 1. Случайная величина X задана плотностью распределения
Задание 6-4. [5[2], C 126], примеры 1-2. Законы распределения НСВ 5.1. Равномерное распределение. Распределение вероятностей непрерывной случайной величины X, принимающей все свои значения из отрезка [а; 6], называется равномерным, если ее плотность вероятности на этом отрезке постоянна, а вне его равна нулю, т. е.
Но, как известно Итак, плотность вероятности непрерывной случайной величины X, распределенной равномерно на отрезке [а; 6], имеет вид:
Задание 6-5. На отрезке [а; b]наугад указывают точку. Какова вероятность того, что эта точка окажется в левой половине отрезка? Обозначим через X случайную величину,— координата выбранной точки. X распределена равномерно (в этом и состоит точный смысл слов: «наугад указывают точку»), а так как середина отрезка [а; 6] имеет координату ^i—, то искомая вероятность равна (см. § 49, п. 2):
Впрочем, этот результат был ясен с самого начала.
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.15.15 (0.005 с.) |


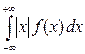 . Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к -¥, а верхнего - к +¥
. Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к -¥, а верхнего - к +¥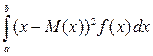

 .
.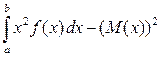 D(x)=
D(x)= 

 Определить математическое ожидание, дисперсию и среднее квадратическое отклонение величины X. Согласно определениям 1 и 2 имеем:
Определить математическое ожидание, дисперсию и среднее квадратическое отклонение величины X. Согласно определениям 1 и 2 имеем:


 » 0,47.
» 0,47.
 Отсюда получим
Отсюда получим =1, то из последнего равенства получим c=1/(b-a)
=1, то из последнего равенства получим c=1/(b-a)