
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергетическая диаграмма. Потери мощностиСодержание книги
Поиск на нашем сайте
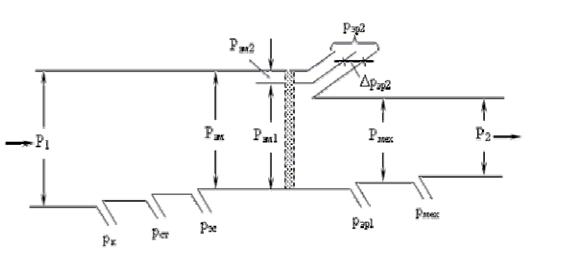
Энергетическая диаграмма несимметричного двухфазного микродвигателя показана на рис. 4.2.
Рис. 4.2. Энергетическая диаграмма несимметричного двухфазного
Здесь обозначено: При эллиптическом поле они равны сумме потерь встали от прямого Потерями в стали ротора при скольженьях, близких к номинальному, можно пренебречь, поскольку частота перемагничивания ротора весьма небольшая Потери в стали статора от поля прямой последовательности рассчитывают обычным порядком [4]. Они пропорциональны квадрату индукции и частоте в степени 1,3:
Потери в стали статора от поля обратной последовательности
где Потери в обмотках А и В статора
В формуле (4.10) должны присутствовать токи статора, полученные с учетом потерь в стали. Эти токи определяются следующим образом [1,5]. Для покрытия потерь в стали двигатель потребляет из сети дополнительный ток, что приводит к увеличению активных составляющих токов статора. Эти увеличения можно рассчитать по следующим формулам:
Прибавляя "добавки" к активным составляющим токов, рассчитанным без учета потерь в стали, получим полные токи фаз статора:
Здесь индексы 1 и 2 означают прямую и обратную последовательности. Потери в обмотке ротора можно определить через электромагнитную мощность (1.28) и скольжение ротора
Из энергетической диаграммы видно, что электрические потери в обмотке ротора от токов обратной последовательности По отношению к полю обратной последовательности машина работает в режиме электромагнитного тормоза, поэтому вся энергия (
Механическая мощность, развиваемая несимметричным двухфазным микродвигателем равна:
Механические потери Полезная мощность на валу микродвигателя
Потребляемая электрическая мощность
КПД микродвигателя
Коэффициенты мощности
Ни в энергетической диаграмме, ни в расчетах не упоминались добавочные потери. Согласно ГОСТ 183–74 они составляют
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 293; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.131.51 (0.008 с.) |

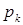 – потери в конденсаторе.
– потери в конденсаторе. 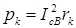 . Активное сопротивление конденсатора
. Активное сопротивление конденсатора 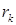 обычно очень мало, так что потерями в нем можно пренебречь,
обычно очень мало, так что потерями в нем можно пренебречь, 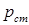 – потери в стали.
– потери в стали.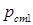 и обратного
и обратного 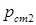 полей [1]:
полей [1]: 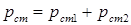 .
.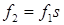 .
.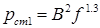 . (4.8)
. (4.8)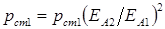 , (4.9)
, (4.9)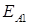 ,
, 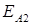 – ЭДС в обмотке
– ЭДС в обмотке 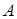 от поля прямой и обратной последовательностей.
от поля прямой и обратной последовательностей.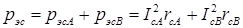 (4.10)
(4.10)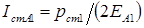 ;
; 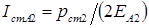 ; (4.11)
; (4.11)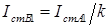 ,
, 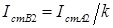 . (4.12)
. (4.12)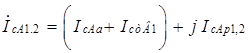 ;
; 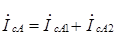 ;
;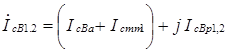 ;
; 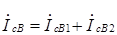 . (4.13)
. (4.13)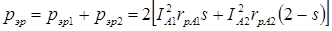 . (4.14)
. (4.14)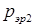 больше электромагнитной мощности обратной последовательности
больше электромагнитной мощности обратной последовательности 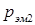 , чего казалось бы не должно быть. Этот парадокс объясняется следующим образом.
, чего казалось бы не должно быть. Этот парадокс объясняется следующим образом.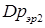 ) также превращается в тепло. Эта часть равна
) также превращается в тепло. Эта часть равна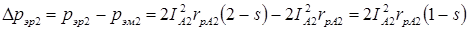 .
.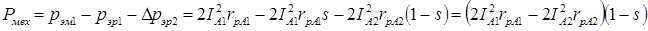
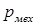 – потери на трение и вентиляцию, определяют по эмпирическим формулам [4], суть которых заключается в том, что эти потери пропорциональны квадрату скорости вращения
– потери на трение и вентиляцию, определяют по эмпирическим формулам [4], суть которых заключается в том, что эти потери пропорциональны квадрату скорости вращения 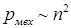 .
.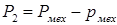 (4.15)
(4.15)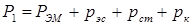 . (4.16)
. (4.16)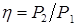 . (4.17)
. (4.17) ;
; 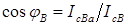 (4.18)
(4.18)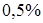 от потребляемой мощности, что практически выходит за пределы точности расчетов микромашин.
от потребляемой мощности, что практически выходит за пределы точности расчетов микромашин.


