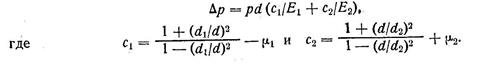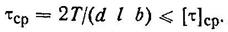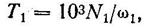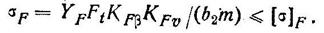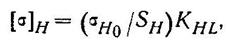Методические указания к выполнению контрольной работы 3

В начале методических указаний к каждой из задач 121—160 даны в квад­ратных скобках ссылки на литературу по списку на с. 61 настоящей работы. Ссылки на справочную таблицу данной работы (с. 112) обозначены словом «приложение» (без указания литературы).

Основной справочной литературой для решения задач является учебник [1] и учебное пособие- [5]. Однако следует иметь в виду, что в указанной литера­туре приняты различные единицы измерения и обозначения расчетных величин. Так, в учебнике [1] приняты единицы измерения системы СИ: длина — метр (м); сила — ньютон (Н); момент силы — ньютон-метр (Н-м); напряжение и давле­ние— Паскаль, Па (Н/м²) и МПа; площадь — квадратный метр (м²) и обозначе­ния основных расчетных величин: F — сила; Т, Т_к и М — моменты соответствен­но вращающий, крутящий и изгибающий; 5 — площадь и др. В пособии [5] приняты единицы измерения, кратные и дольные от единиц СИ; длина — мил­лиметр (мм);, сила — ньютон (Н); момент силы — ньютон-миллиметр (Н-мм); напряжение и давление ^v— ньютон на миллиметр квадратный (Н/мм²) (1 Н/мм²=1 МПа = 10⁶ Па); площадь — квадратный миллиметр (мм²) и обозна­чения расчетных величин: Р — сила, М — момент вращающий и изгибающий, М_к — момент крутящий, F — площадь и др.

Решения задач можно выполнять, пользуясь или только учебником [1], или только пособием [5], применяя принятые в них единицы измерения и обозна­чения расчетных величин. Предпочтительнее учебник [1]. При этом надо иметь в виду, что результаты расчетов по формулам учебника получаются: при опре­делении линейных размеров — в метрах (м); при определении напряжений и дав­лений—в Паскалях (Па), которые необходимо переводить в миллиметры (мм) и мегапаскали (МПа). Некоторые задачи можно решить, пользуясь пособием [4] и задачником [3].

Следует иметь в виду, что при выборе твердости заданного материала для определения допускаемых напряжений рекомендуется: при расчете прямозубых передач твердость материала шестерни выбирать на 20—30 единиц НВ больше, чем для колеса, т.е. HBi>HB₂+20—30, что обеспечивает лучшую приработку зубьев и примерно равный износ шестерни и колеса; при расчете косозубых и шевронных передач HBi>HB₂+50—80, что позволяет существенно повысить нагрузочную способность этих передач.

 

К задаче 121. Литература: [1, с. 12—19, пример 1]; [2, с. 220—223, пример 23.1].

Рекомендуемый порядок решения:

1. По табл. 1.1 учебника [1] или с. 35 задачника [3] выбрать допускаемые

напряжения растяжения [σ]_р и среза [t]_cf-

2. Из условия прочности на растяжение определить необходимую ширину полосы Ь, которую затем округлить до ближайшего большего значения нор-мальных линейных размеров по ГОСТ 6636—69 (с. 229 учебника [1] или с. 95 пособия [4]).

3. Из условия прочности углового шва на срез определить общую расчет­ную длину швов l _ш сварного соединения.

4. Принять длину лобового шва l_Л равной ширине полосы b и определить длину фланговых швов: l ф=(l _ш— l _л)/2.

 

К задаче 122. Литература: [1, с. 20—26, пример 2]; [2, с. 224—225]; [4, с. 151—152, пример 8.1].

Рекомендуемый порядок решения:

1. Принять для стали модуль упругости E₁ = E ₂ = 2-10⁵-10⁶ Па и коэффи­циент Пуассона μ₁ = μ₂ = 0,3.

2. Определить контактное давление р на посадочной поверхности;

где р в Па; Т в Н-м; F в Н; d и l в м.

3. Определить расчетный натяг ∆р:

Величину ∆р выразить в микрометрах (мкм).

4. Принять высоту микронеровностей посадочных поверхностей R_zl = Rz2= 10 мкм и определить требуемый натяг ∆ _т в мкм:

5. По величине ∆ _т выбрать посадку по стандарту СТ СЭВ 144—75 (при­ложение 1) и определить наименьший натяг ∆ _min и наибольший натяг ∆max. При выборе посадки надо стремиться, чтобы разница между ∆ _т и ∆ _min была, наименьшей.

 

К задаче 123. Литература: [1, с. 27—53, пример 4]; [2, с. 225—237].

Рекомендуемый порядок решения:

II. По табл. 3.3 учебника [1]для заданного класса прочности материала болта определить предел текучести σ_т и марку стали.

2. По табл. 3.4 учебника [1] для заданного номинального диаметра резьбы принять значение требуемого коэффициента запаса прочности [n_т], а затем определить допускаемое напряжение растяжения [σ]_Р = σ _т/[n_т].

3. Определить расчетный диаметр резьбы болта d_p=d —0,94р, где р — шаг резьбы (табл. 3.1 учебника [1] или приложение II пособия [2]).

4. Определить из условия прочности на растяжение с учетом скручивания болта расчетное усилие затяжки одного болта:

5. Определить требуемое число болтов z = 2KT/(DofF_расч). Величину z ок­руглить до ближайшего большего четного числа.

 

К задаче 124. Литература та же, что и к задаче 123. Рекомендуемый порядок решения:

l. По табл. 3.3 учебника [1] для заданного класса прочности материала болта определить предел текучести а_т и марку стали.

2. По табл. 3.4 учебника [1] принять значение требуемого коэффициента прочности [п_т], ориентировочно приняв диаметр резьбы болта в интервале 16... 30 мм, а затем определить допускаемое напряжение растяжения [σ]_р = σт/[nт].

3. Определить с учетом скручивания расчетное усилие затяжки одного болта:

4. Определить из условия прочности на растяжение расчетный диаметр резьбы:

5. По табл. 3.1 учебника [1] или по приложению и пособия [2] принять резьбу. Например, принимаем резьбу М24 с шагом p =3 мм, для которой d_p≈d-0,94p.

 

К задаче 125. Литература та же, что и к задаче 123.

Для определения диаметра болтов, поставленных с зазором, последователь­ность решения задачи 125 аналогична последовательности решения задачи 124.

Для определения требуемого числа болтов z₂, установленных без зазора, необходимо:

1. Определить допускаемое напряжение на срез [т]_Ср=0,25σ_т.

2. Принять диаметр ненарезанной части стержня болта d₀ на 1 мм больше номинального диаметра резьбы болта, поставленного с зазором.

3. Из условия прочности на срез определить поперечную (сдвигающую) силу F_r приходящуюся на один болт, поставленный без зазора: F_r = πd(2(0))τ_Cp/4.

4. Определить требуемое число болтов z₂ = 2KT/(D₀F_r). Величину z₂ округлить до ближайшего большего четного числа.

 

К задаче 126. Литература: [1, с. 27—53]; [7, с. 110—111]; [11, § 42].

Последовательность решения задачи 126 до п. 5 аналогична последова­тельности решения задачи 123.

В п. 5 определить требуемый момент сил трения T_Тр = zFрасчfd, а затем определить допускаемое значение силы [F] — Т_тр/(1,25 l).

 

К задаче 127. Литература та же, что и к задаче 126.

Рекомендуемый порядок решения:

1. Определить предел текучести σ_т и допускаемое напряжение растяжения [σ]_р (см. п. 1 и 2 задачи 124).

2. Определить требуемый момент сил трения T_тр=l,2Fl.

3. Определить требуемое усилие затяжки одного болта:

4. С учетом скручивания болта определить расчетное усилие затяжки

Fрасч=1,3F0

5. Дальнейший порядок решения см. п. 4 и 5 задачи 124.

 

К задаче 128. Литература: [1, с. 145—152, пример 23]; [2, с. 301—303]; (4, § 5.2, пример 5.2].

Рекомендуемый порядок решения:

1. Выбрать допускаемое давление в резьбе [р] и допускаемые напряжения для материала гайки: на смятие [σ]_см и на растяжение [ σ]_р (с. 151 учебника [1]).

2. Определить средний диаметр резьбы из условия износостойкости вин­товой пары:

 

По ГОСТ 9484—73 (табл. 3.2 учебника [1]) принять размеры резьбы (d, d1, d₂ , p).

3. Проверить условие самоторможения винтовой пары γ‹ρ’Для этого надо определить угол подъема резьбы γ = p /(πd₂) и приведенный угол трения р'= arctg f /cos 15°. Значение коэффициента трения принять по табл. 5.1 учебника [1].

4. Определить высоту гайки Н и число витков резьбы z в гайке: Н = ψ_H d2, z = Н/р. Если по расчету получилось z > 10, то необходимо принять резьбу с другими размерами и повторить расчет.

5. Определить наружный диаметр гайки D, диаметр буртика гайки D₁ и принять высоту буртика гайки а.

К задаче 129. Литература: [1, с. 240—247, примеры 40 и 41]; [2, с. 238—240]; [4, с. 149—150]; [5, § 6.4].

Рекомендуемый порядок решения:

1.По табл. 11.4 учебника [1], или по табл. 8.14 пособия [4], или по табл. 6.9 пособия [5] по заданному диаметру вала d выбрать размеры сечения шпонки.

2. По табл. 11.6 учебника [1] или с. 102 пособия [5] в зависимости от мате­риала зубчатого колеса и характера нагрузки выбрать допускаемое напряже­ние смятия [σ]см.

3. Определить рабочую длину шпонки l_p исходя из условия прочности шпо­ночного соединения на смятие:

4. Вычислить длину шпонки со скругленными торцами l=l_p + b и округлить ее до ближайшего большего стандартного значения (см. примечание к табл. 11.4 учебника [1] или примечание 1 к табл. 6.9 пособия [5]).

5. Определить требуемую длину ступицы l_СТ зубчатого колеса, которая должна быть больше длины шпонки на 5... 10 мм, т.е. l_ст = l+(5... 10) мм.

 

К задаче 130. Литература та же, что и к задаче 129. Рекомендуемый порядок решения:

1. По табл. 6.10 пособия [5] выбрать размеры шпонки: b, h, l и t1.

2. По табл. 11.6 учебника [1] или с. 102 пособия [5] в зависимости от ма­териала зубчатого колеса и характера нагрузки выбрать допускаемое напря­жение смятия [σ]_см. Допускаемое напряжение на срез шпонки [τ]_ср ≈ 0,6 [σ]_см-

3. Проверить прочность шпонки на срез по условию

4. Проверить шпоночное соединение на смятие по условию

 

К задаче 131. Литература: [1, с. 69—104, пример 15]; [2, с. 243—268]; 5, § 3.3].

Рекомендуемый порядок решения:

1. Определить вращающий момент на валу шестерни:

где N₁ в кВт, 7, в Н-м.

2. Определить число зубьев колеса z% предварительно задаться числом зубьев шестерни Z1 (рекомендуется Z1 = 18... 22). -

3. По табл. 3.3 пособия [5], или по табл. 6.4 учебника [1], или по табл. 4.1 пособия [4] выбрать НВ, σ_в и σ_т заданного материала шестерни и колеса.

4. Определить допускаемое напряжение изгиба для шестерни [σ]F1, и ко­леса [ σ ]F2:

где σ _F0 = 1,8 НВ в МПа —предел выносливости зубьев по излому (табл. 6.7 учебника [1], или табл. 4.3 пособия [4], или табл. 3.9 пособия [5]); S_f— коэф­фициент безопасности для зубчатых колес, изготовленных из поковок и штам­повок, и Kf_L — коэффициент долговечности при длительной работе передачи (с. 96 учебника [1] или с. 47 пособия [4] или с. 37 пособия [5]).

5. В зависимости от числа зубьев z₁ и z₂ выбрать коэффициенты формы зуба шестерни Y_f1 и колеса Y_f2 (табл. 6,8 учебника [1], или с. 265 пособия [2], или с 35 пособия [5]). Произвести сравнительную характеристику прочности зубьев на изгиб по отношениям [ σ ]_f1/Y_Fl и [ σ ]_F2/Y_f2. Дальнейший расчет передачи выполнять по тому из колес пары, у которого меньше это соотношение (зубья менее прочны).

6. Принять расчетные коэффициенты: коэффициент ширины венца колеса ψ_bd (табл. 6.9 учебника [1] для консольного расположения шестерни относи­тельно опор или табл. 5 пособия [2] при НВ₂ ≤ 350); коэффициент неравно­мерности нагрузки при расположении вала на шарикоподшипниках и консоль­ном расположении колес К_fβ (табл. 6.10 учебника [1] или табл. 3.7 пособия[5]).

7. Определить окружной модуль зубьев из условия прочности зубьев на изгиб:

где т в м; Т₁ в Н-м; [σ]_F в Па.

Полученную величину m округлить до ближайшего большего стандартного значения (табл. 6.1 учебника [1] или с. 30 пособия [5]).

8. Определить геометрические размеры передачи: d, d_a, a_w, b₁ и b₂

9. Определить окружную силу F_t = 2T₁/d1 в Н

10. Определить окружную скорость зубчатых колес ν = ω1d1/2-10³ м/с и назначить степень точности.

11. Принять коэффициент динамической нагрузки K_Fv (с. 102 учебника [1], или табл. 4.13 пособия [4], или табл. 3.8 пособия [5]).

12. Проверить зубья на выносливость при изгибе:

Допускается перегрузка зубчатой передачи до 5%, а недогрузка — до 10%. В противном случае изменить b₂ или даже т и повторить проверочный расчет

 

К задаче 132. Литература: [1, с. 69—117, пример 17]; [2, с. 243—268]; [б, § 3.3].

Последовательность решения задачи 132 аналогична последовательности ре­шения задачи 131, различие в следующих пунктах.

В п. 5 необходимо задаться углом наклона зубьев β (рекомендуется (β = 8...18°) и найти эквивалентное число зубьев шестерни z_vl ==z₁/cos³ β и коле­са z_v2 = z₂/cos³ β , затем по величинам z_vl и z_v2 выбрать коэффициент формы зуба шестерни Y _F1 и колеса Y _F2 (табл. 6.8 учебника [1], или с. 265 пособия [2], или с. 35 пособия [5]) и произвести сравнительную характеристику проч­ности зубьев на изгиб по отношениям [σ]_F1/ Y_F1 и [σ]_F21Y_F2. Расчет передачи выполнять по тому из колес, для которого меньше это отношение.

В п. 7 определить нормальный модуль зубьев:

где т_п в м; Т₁ в Н • м; [σ]_F в Па.

Полученную величину m_п округлить до ближайшего большего стандарт­ного значения (табл. 6.1 учебника [1] или с. 30 пособия [5]).

В п. 11 принять коэффициент динамической нагрузки Kfv косозубой пере­дачи (с. 1102 учебника [1], или табл. 4.13 пособия [4], или табл. 3.8 пособия [5]).

В п. 12 проверку зубьев на выносливость при изгибе выполнить по усло­вию

 

К задаче 133. Литература: [1, с. 69—122]; [2, с. 143—268]; [5, §3.3].

Последовательность решения задачи 133 аналогична последовательности ре­шения задачи. 131, различие в следующих пунктах.

В п. 5 необходимо задаться углом наклона зубьев β (рекомендуется р = 25... 40°) и найти эквивалентное число зубьев шестерни z_v1 = z1/cos³ βи колеса z_v2 = z₂/cos³ β, затем по величинам z_vl и zv2 выбрать коэффициенты формы зуба шестерни Y_F1 и колеса Y_F2 (табл. 6.8 учебника [1], или с. 265 пособия [2], или с. 35 пособия [5]) и произвести сравнительную характеристику прочности зубьев на изгиб по отношениям [σ]_F1lY_Fl и [σ]_F2l Y_F2 Расчет пере­дачи выполнять по тому из колес, для которого меньше это отношение.

В п. 6 при выборе коэффициента ψbd учесть примечание 2 к табл. 6.9 учебника [1]. Выбор коэффициента К_Fβ производится так же, как и при ре­шении задачи 131.

В п. 7 определить нормальный модуль т_п по формуле, приведенной к за­даче 132.

В п. 11 для шевронной передачи, как и для косозубой, принять коэффи­циент динамической нагрузки K_Fv (с. 102 учебника [1], или табл. 4.13 пособия [4], или табл. 3.8 пособия [5]).

В п. 12 проверку зубьев на выносливость при изгибе выполнить по усло­вию, приведенному к задаче 122.

 

К задаче 134. Литература: [1, с. 69—129, пример 20]; [2, с. 269—2731; [5, § 3.4].

Последовательность решения задачи 134 аналогична последовательности ре­шения задачи 131, различие в следующих пунктах.

В п. 2 задаться числом зубьев шестерни Z1 (рекомендуется z1 = 18... 28) и определить число зубьев колеса z₂.

В п. 5, по передаточному числу, определить углы при вершинах делитель­ных конусов δ₁ и δ₂, а затем вычислить эквивалентное число зубьев шестерни z v1 =z1 /cosδ 1 и колеса z_v2 = z2/cosδ₂ и по их величине выбрать коэффициен­ты формы зуба шестерни Y_F1 и колеса Y _F2 (табл. 6.8 учебника [1],или с. 265 пособия [2], или с. 35 пособия [5]). Далее произвести сравнительную ха­рактеристику прочности зубьев на изгиб по отношениям [σ]F1/YF2 и [σ]_F2IY_F2. Расчет передачи выполнять по тому из колес, для которого меньше это от­ношение.

В п. 6 принять: коэффициент ψ bd для консольного расположения шестерни относительно опор (табл. 6.9 учебника [1] и табл. 5 пособия [2]) и коэффици­ент КFβ, предполагая расположение вала шестерни на роликоподшипниках (табл. 6.10 учебника [1] или табл. 3.7 пособия [5]).

В п. 7 определить средний модуль зубьев:

где т в м; T1 в Н *м; [σ]F в Па. Полученную величину по ГОСТу не ок­руглять.

В п. 8 определить средний делительный диаметр шестерни d1 = тz₁ шири­ну зубчатого венца b = ψbd(d1) внешний окружной модуль т_е — т + (b sin δ1)/z1 (округлять т_е до стандартного значения для конических колес необяза­тельно) и основные геометрические размеры передачи (d_e1, d_e2, d_ae1, d_ае2, Re и R).

В п. 9 определить окружную силу F_t = 2T1/d1.

В п. 12 проверку зубьев на выносливость при изгибе выполнять по усло­вию σF = _FF_tK_FβK_Fv/(0,85 bm) ≤ [σ]_F.

 

К задаче 135. Литература: [1, с. 69—110, пример 16]; [2, с. 243—268]; [4, § 4.4]; [5, § 3.2].

Рекомендуемый порядок решения:

1. Определить вращающие моменты на валу шестерни Т₁ =10(3)N1/ω1и на валу колеса T₂ = Т₁ и, где N1 в кВт,- Т в Н • м.

2. По табл. 3.3 пособия [5],или по табл. 6.4 учебника [1], или по табл. 4.1 пособия [4] выбрать НВ, σ_b и σ_т заданного материала шестерни и колеса.

3. Определить допускаемое контактное напряжение для материала колеса как менее прочного элемента передачи:

где σH0 = 2 НВ₂ + 70 в МПа — предел контактной выносливости (табл. 6.5 учебника [1], или табл. 4.3 пособия 14], или табл. 3.2 пособия [5]); принять значения коэффициентов: безопасности S_H для нормализованных и улучшен­ных сталей и долговечности K_HL при длительной работе редуктора (с. 94 и 95 учебника [1], или с. 45 пособия¹ [4], или с. 28 пособия [5].

4. По табл. 6.9 учебника [1] или табл. 5 пособия [2] при симметричном расположении колес относительно опор принять коэффициент ψbd и вычислить коэффициент ширины венца колеса ψb_a = 2ψbd/(и + I), округлив его до стан­дартного значения (с. 108 учебника [1]), затем по табл. 6.11 учебника [1] или по табл. 3.5 пособия [5] в зависимости от ^ftd принять значение коэффициента неравномерности распределения нагрузки по длине контактных линий Кц$-

5. Определить межосевое расстояние из условия контактной выносливости рабочих поверхностей зубьев:

где a_w в м; Т₁ в Н • м; [σ]_н в Па.

Полученную величину а_ю округлить до стандартного значения (с. 108 учеб­ника [1], или с. 263 пособия [2], или с. 30 пособия [5]).

6. Задаться величиной модуля зубьев m=(0,01... 0,02) aώ „ и принять его по стандарту (табл. 6.1 учебника [1] или с. 30 пособия [5]). В силовых переда­чах не рекомендуется иметь m<2 мм.

7. Определить числа зубьев шестерни и колеса:

При этом должно соблюдаться условие z1≥ z_min = 17.

8. Определить основные геометрические размеры передачи: d₁ d2, прове­рить a_w, d_a1 d₂, b₂ и b1 и окружную силу F_t. Диаметры делительных окруж­ностей вычислять с точностью до 0,01 мм.

9. Определить окружную скорость зубчатых колес v = ώ1d1/2 • 10³ и по табл. 6.2 учебника [1] или с. 49 пособия [4] назначить степень точности их изготовления.

10. Уточнить коэффициент ширины венца колеса ψbd = b2/d1. По величине ψbdпринять Кhβ (справочные таблицы указаны в п. 4). Коэффициент дина­мической нагрузки K_Hv (с. 107 учебника [1], или табл. 4.11 пособия [4], или табл. 3.6 пособия [5]).

11. Проверить контактную выносливость рабочих поверхностей зубьев по условию

Допускается недогрузка передачи до 10% иди перегрузка до 5%. Если условие прочности (σ_h ≤ [σ]_h) не выполняется, то надо увеличить ширину венца колеса b₂, не выходя за пределы рекомендуемых значений ψbd уменьшения σ_н можно увеличить a_w иди принять другие материалы, но в этом случае необходимо повторить расчет.

12. Определить радиальную силу F_r в зацеплении.

 

К задаче 136. Литература: [1, с. 69—118, пример 18]; [2, с. 243—268]; [4, § 4.4, с. 214—215]; [5, § 3.2, с. 185—1187, с. 209—211].

Последовательность решения задачи 136 аналогична последовательности ре­шения задачи 135, различие в следующих пунктах.

В п. 3 определить допускаемые контактные напряжения для материала шестерни и колеса:

В качестве расчетного принять условное допускаемое контактное напря­жение [σ]_и = 0,45 ([ σ ]_h1 [σ]_Н2). При этом должно выполняться условие [σ]_н ≤ 1,23[ σ ]h₂. Если это условие не выполняется, то за допускаемое кон­тактное напряжение принимают [σ]_н = 1,23[ σ ]h_2.

В п. 5 определить межосевое расстояние:

где a_w в м; T1 в Н-м; [ σ]_н в Па. Полученную величину округлить до стан­дартного значения.

В п. 6 задаться величиной нормального модуля зубьев т_п = (0,01ч/0,02)a_w и принять его по стандарту.

В п. 7 задаться предварительно углом наклона зубьев β (рекомендуется β = 8...18°)и определить число зубьев шестерни z₁ = 2a_w cos β /[(u + 1) т_п] и колеса z2, а затем уточнить значение угла β по зависимости cos β = {z₁ + z₂) mn/(2a_w). Значения cos β вычислять с точностью до четырех знаков.

В п. 10 уточнить коэффициент ψ_bd = b₂/d₂ и вычислить коэффициенты Khb, Khv и Kh_α. По величине ψ_bd принять Кh β. Коэффициент K_Hv (с. 118 учебника [1], или табл. 4.11 пособия [4], или табл. 3.6 пособия [5]). Коэффи­циент неравномерности распределения нагрузки между зубьями Kh_α (с. 118 учебника [1], или табл. 4.11 пособия [4], или табл. 3.4 пособия [5])-

В п. 11 проверить контактную выносливость рабочих поверхностей зубьев по условию

В п. 12 определить действующие в зацеплении радиальную F_r и осевую F_a силы.

 

К задаче 137. Литература: [1, с. 69—122]; [2, с. 243—268]; [4, § 4.4]; [5, § 3.2].

Последовательность решения задачи 137 аналогична последовательности ре­шения задачи 136. Шевронное колесо представляет собой сдвоенное косозубое колесо, выполненное как одно целое. Проектировочный и проверочный расчеты шевронной передачи выполняются по тем же формулам, что и косозубой пере­дачи. Однако для шевронной передачи рекомендуется коэффициент ψbd прини­мать в 1,3 раза больше, чем для косозубой (примечание 2 к табл. 6.9 учебни­ка [1]), а угол наклона зуба β =25... 40^o. В шевронной передаче осевая сила Fa=0.

 

К задаче 138. Литература: [1, с. 69—129 и с. 134, пример 21]; [2. с. 269—274]; [4, § 4,5; 5, § 3.4, пример расчета зубчатой передачи редуктора на с. 214—217].

Рекомендуемый порядок решения:

1. Определить вращающие моменты на валу шестерни T₁ =10³N₁/ω₁ и на валу колеса Т₂ = T₁u, где N1 в кВт, Т в Н*м.

2. По табл. 3.3 пособия [5], или по табл. 6.4 учебника [1], или по табл. 4 пособия [4] выбрать НВ, σ _b и σ_т заданного материала шестерни и колеса.

3. Определить допускаемое контактное напряжение для материала колеса как менее прочного элемента передачи:

где σh ₀=2hb₂+70 в МПа — предел контактной выносливости (табл. 6.5 учебника [1], или табл. 4.3 пособия [4], или табл. 3.2 пособия [5]); принять значения коэффициентов: безопасности S_H для нормализованных И улучшенных сталей и долговечности KH_L при длительной работе редуктора (с. 94 и 95 учебника [1], или с. 45 пособия [4], или с. 28 пособия [5]).

4. По табл. 6.9 учебника [1] и по табл. 5 пособия [2] при консольном расположении шестерни относительно опор (опоры вала шестерни ролико­подшипники) принять ψpd затем по табл. 6.11 учебника [1] или по табл. 3.5 пособия [5] принять значение коэффициента неравномерности распределения нагрузки по длине контактных линий KH β.

5. Определить средний делительный диаметр шестерни d₁ ширину зубчатого венца b и внешний делительный диаметр колеса d_e2:

Полученную величину d_e2 и b округлить до ближайшего стандартного значения ([4, табл. 4.15]; табл. 6.12 учебника [1] или приложение IV посо­бия [2]).

6. Определить число зубьев шестерни z_i и колеса z₂. Из рекомендуемого интервала z₁ = 18... 28 принять z₁ и определить г₂, затем уточнить и' = z₂jz₁. отклонение которого от заданного не должно быть больше ±3%.

7. Определить внешний окружной модуль т_е = d_e2\z₂ (округлять т_е до стандартного значения для конических колес не обязательно).

8. Определить углы делительных конусов F_t и 5₂ и основные геометри­ческие размеры колес: <1_еъ d_ael, d_ae2, R_e и R.

9. Определить окружную силу Ft; средний окружной модуль т. = d_x\z{, среднюю окружную скорость зубчатых колес v = (Ojdj/2-10³. По табл. 6.2 учебника [1] или с. 49 пособия [4] назначить степень точности.

10. Уточнить коэффициент ширины зубчатого венца по среднему диаметру ty_bd = Ш, и вычислить коэффициенты Кц$ и Kfj_v- По величине ф^ принять /С//р (справочные таблицы указаны в п. 4). Коэффициент динамической нагрузки Ktf_v (с. 107 учебника [1], или табл. 4.11 пособия [4], или табл. 3.6 посо­бия [5]).

11. Проверить контактную выносливость рабочих поверхностей зубьев по условию

Допускается недогрузка передачи до 10% или перегрузка до 5%. Если условие прочности (σh ≤ [σ]_h) не выполняется, то надо увеличить ширину зубчатого венца b, не выходя за пределы рекомендуемых значений ψbd

12 Определить силы в зацеплении: радиальные F_r1 и F_r2 и осевые F_al, F_a2.

К задаче 139. Литература: [1, с. 155—173,. пример 29]; [2, с. 304-314. пример 32.1 l ]; [5, § 4.1—4.4, с. 237—240]; [4, § 5.1]. Рекомендуемый порядок решения: 1. Определить вращающие моменты на валах редуктора:

где N1 в кВт; Т в Н-м; η — КПД червячного редуктора. Ориентировочно η = 0,95 (1— и /200).

2. Выбрать число витков червяка z₁ таким, чтобы z₂ — z1и≥28, и опре­делить z2.

3. Выбрать допускаемое контактное напряжение [σ]_н для заданного материала колеса. Для безоловянистых бронз [σ]_н зависит от скорости сколь­жения v_s, которой в начале расчета необходимо задаться из соотношения v_s — 2,5... 5 м/с, и по табл. 8.4 учебника [1], или по табл. 5.4 пособия [4], или по табл. 4.9 пособия [5] выбрать величину [σ]_н.

4. Предварительно задаться коэффициентом диаметра червяка q. Рекомен­дуется в начале расчета принимать q=10, так как это значение имеется прак­тически для всех стандартных модулей. Принять коэффициент нагрузки K=1.1.

5. Определить межосевое расстояние из условия контактной выносливости зубьев червячного колеса:

где a_w в м; T₂ в Н-м; [σ]_н в Па.

6. Определить модуль т =» 2a_w\{q + z₂) и принять его по стандарту (с. 160 учебника [1], или приложение V пособия [2], или табл. 4.1 и табл. 4.2 посо­бия [5]). По указанным таблицам проверить сочетание принятых т и q. При необходимости принять другое значение т или q.

7. Уточнить межосевое расстояние при стандартных значениях т и q; a_w — m(q + z₂)l2.

8. Определить основные геометрические размеры червяка: d_1, d_a1, df_l, b₁ и γ(tg γ=z1/q) и червячного колеса: d₂, d_a2, df₂, d_aM2 и b₂.

9. Определить скорость скольжения v_s — a>ω1d1/ (2 • 10³cos γ) и по табл. 8.1 учебника [1] с учетом примечания 2 или по табл. 4.4 пособия [5] с учетом примечания 2 принять значение угла трения р'.

10. Вычислить расчетное значение КПД передачи η ' = 0,95 tg γ /[tg (γ + р')] и уточнить вращающий момент на валу колеса Т'2 = Т1и η'

11. Определить силы, действующие в зацеплении червячной передачи: Ft1= F_a2; Ft2 = Fa1; Fr1= Fr2

12. По таблицам, указанным в п. 3, уточнить [σ]_н в зависимости от по­лученной v_s и проверить контактную выносливость зубьев червячного колеса по условию

Допускается недогрузка до 10%, а перегрузка до 5%.

 

К задаче 140. Литература та же, что и к задаче 135. Рекомендуемый порядок решения:

1. Для заданного материала шестерни и колеса выбрать НВ σ _b и σ _t (cm. п. 2 к задаче 135).

2. Определить допускаемые напряжения. Допускаемое контактное напря­жение (см. п. 3 к задаче 135). Допускаемое напряжение изгиба для шестерни [σ]F1 и колеса [σ]_F2 (см. п. 4 к задаче 131).

3. Принять коэффициент ψbd, как для симметричного расположения колес, и вычислить коэффициент ψba- Принять коэффициент Khβ (см. п. 4 к задаче 135).

4. Определить вращающий момент Т₁ из формулы для определения межосевого расстояния a_w (см. п. 5 к задаче 135).

5. Определить мощность, которую может передать редуктор: N₁ = T1ω1/10³, кВт.

6. Определить диаметры делительных окружностей шестерни d₁ = 2a_w/{u + 1) и колеса d₂ и ширину венца колеса b₂ = ψbaAw

7. Задаться величиной модуля зубьев (см. п. 6 к задаче 135).

8. Определить число зубьев z₁ = d₁/m и z2 = d₂/m, при этом u = z2/z1 должно отличаться от заданного не больше чем ±2,5% при и ≤ 4,5 и не боль­ше чем ±4% при и > 4,5. Если эти рекомендации не выполняются, необходимо принять другое стандартное значение модуля.

9. Определить окружную силу F_t = 2T₁/d₁ в Н.

10. Выбрать коэффициенты формы зуба шестерни У_F1 и колеса Y_F2 и про­извести сравнительную характеристику прочности зубьев (см. п. 5 к задаче 131).

11. По принятому коэффициенту ψbd(см. п. 3) выбрать коэффициент не равномерности нагрузки Кр β(табл. 6.10 учебника [1] или табл. 3.7 пособия [5]).

12. Принять коэффициент динамической нагрузки Kp_v (с. 102 учебника [1] -или табл. 3.8 пособия [5]).

13. Проверить зубья на выносливость при изгибе:

 

К задаче 141. Литература та же, что и к задаче 136. Рекомендуемый порядок решения:

1. Для заданного материала шестерни и колеса выбрать НВ, σ_b и σ _т (см. п. 2 к задаче 135).

2. Определить допускаемые напряжения. Допускаемое контактное напря­жение (см. п. 3 к задаче 136). Допускаемое напряжение изгиба для шестерни [σ]F1 и колеса [σ]F2 (см. п. 4 к задаче 131).

3. Определить передаточное число и и диаметры делительных окружно­стей d1 и d₂.

4. Определить межосевое расстояние a_w и округлить его до стандартного значения (с. 108 учебника [1], или с. 263 пособия [2], или с. 30 пособия [5]) и вычислить ширину венца колеса b₂ = ψbaAw.

5. Определить коэффициент ширины венца колеса ψbа и коэффициент неравномерности распределения нагрузки К_Hβ (см. п. 4 к задаче 135).

6. Определить вращающий момент T1 из формулы для определения межосевого расстояния a_w (см. п. 5 к задаче 136).

7. Определить мощность N₁ которую может передать редуктор (см. п. 5 к задаче 140).

8. Определить окружную силу F_t =2T₁/d1 в Н.

9. Определить угол наклона зубьев β по зависимости cos β = (z1 +z2) m_n/(2a_w). Значения cos β вычислять с точностью до четырех или пяти знаков.

10. Вычислить эквивалентное число зубьев шестерни z_vl = z1/cos³ βи ко­леса z_v2 =z₂/cos³ β, затем по величинам z_v1 и z_v2 выбрать коэффициент фор­мы зуба шестерни Y_Fl и колеса Y _F2 (табл. 6.8 учебника [1], или с. 265 посо­бия [2], или с. 35 пособия [5]) и произвести сравнительную характеристику прочности зубьев на изгиб по отношению [σ]_F1/ Y_F1 и [σ]_F2/ Y_F2. Проверять

зубья на выносливость при изгибе надо по тому из колес, для которого мень­ше это отношение.

11. Выбрать коэффициент динамической нагрузки К_Fv (см. п. 12 к задаче 140).

12. Выполнить проверку зубьев на выносливость при изгибе (см. п. 12 к задаче 132).

 

К задаче 142. Литература та же, что и к задаче 137.Рекомендуемый порядок решения:

1. Для заданного материала шестерни и колеса выбрать НВ, σ b и σ _т (см. п. 2. к задаче 135).

2. Определить допускаемые напряжения. Допускаемое контактное напря­жение (см. п. 3 к задаче 136). Допускаемое напряжение изгиба для шестерни [ σ ]F1и колеса [σ]_F2 (см. п. 4 к задаче 131).

3. Принять коэффициент ψbd, как для симметричного расположения ко­лес, с учетом примечания 2 к табл. 6.9 учебника [1] и вычислить коэффици­ент ψ _ba. По величине ψbd принять коэффициент Кhβ (см. п. 4 к задаче 135).

4. Определить вращающий момент Т1 и мощность N₁ которую может передать редуктор (см. п. 6 и 7 к задаче 141).

5. Определить диаметры делительных окружностей шестерни d1 = 2a_w/(u + 1) и колеса d₂ и ширину венца колеса b₂ = ψ _ba aw

6. Определить окружную силу F_t = 2 T1/d1 в Н.

7. Задаться предварительно углом наклона зубьев β (рекомендуется β = 25...40°) и модулем зубьев из соотношения т_п = (0,01... 0,02) a_w. Модуль т_п принять по стандарту (см. п. 6 к задаче 135).

8. Определить число зубьев шестерни z₁ = 2a_w cos β /[(u + 1)mn]и коле­са z₂, при этом u = z₂/z1 должно отличаться от заданного не больше величин, указанных в п. 8 к задаче 140.

9. Дальнейший порядок решения задачи см. п. 9, 10, 11 и 12 к задаче 141.

 

К задаче 143. Литература та же, что и к задаче 138. Рекомендуемый порядок решения:

1. Для заданного материала шестерни и колеса выбрать НВ, σ_b и σ _T (см. п. 2 к задаче 135).

2. Определить допускаемые напряжения. Допускаемое контактное напря­жение (см. п. 3 к задаче 138). Допускаемое напряжение изгиба для шестерни [σ]_Fl и колеса [ σ ]_F2 (см. п. 4 к задаче 131).

3. Принять ширину зубчатого венца b ([4, табл. 4.15]; табл. 6.12 учебника [1] или приложение IV пособия [2]) и определить средний делительный диа­метр шестерни d1 из формулы

4. Принять коэффициенты ψbd и Кhβ (см. п. 6 к задаче 134) и из формулы для определения d_x определить вращающий момент T₁ (см. п. 5 к задаче 138).

5. Определить мощность N₁ которую