
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос. Параметры идеального газа.Стр 1 из 8Следующая ⇒
Вопрос. Параметры идеального газа. Идеальный газ - идеализированная модель, в которой считают, что: - собственный объем молекул пренебрежительно мал по сравнению с объемом сосуда. - между молекулами газа отсутствуют силы взаимодействия. - столкновение молекул газа между собой и стенками сосуда абсолютно упругие.
Термодинамическая температура. T - Измеряется в кельвинах.
V-объём [м3] Например
M[кг/моль] Водород Гелий Азот Воздух Кислород Аргон Ar
Удельный объем это объем единицы массы; это величина обратная плотности.
Термодинамическая система это совокупность макроскопических тел которые взаимодействуют и обмениваются энергией как между собой так и с окружающими телами. Состояние системы задается термодинамическими параметрами. Вопрос. Законы идеального газа.
Этому закону подчиняется изотермический процесс, то есть процесс, протекающий при постоянной температуре.
Чем дальше график от системы координат, тем выше на нем температура.
Кривая, изображающая зависимость между величинами P и V, называется изотермой. - Законы Гей-Люссака: а) Объем данной массы газа при постоянном давлении изменяется линейно с температурой.
б) Давление данной массы газа при постоянном объёме растет линейно с температурой.
- Закон Авогадро: Моли любых газов при одинаковых температуре и давлении занимают одинаковые объёмы.
По определению: в одном моле различных веществ содержится одно и тоже число молекул называется постоянной Авогадро.
- Закон Дальтона: Давление смеси газов равно сумме парциальных давлений входящих в смесь газов.
Парциальное давление это давление которое оказывал бы газ входящий в смесь если бы он один занимал объем равный объему смеси при той же температуре. Вопрос. Изо-процессы с точки зрения уравнение Клапейрона-Менделеева.
- Изотермический процесс Запишем уравнение Клапейрона-Менделеева
2.
- Изохорный процесс.
Вопрос. Работа газа. Рассмотрим газ, находящийся под поршнем.
Р – давление, S – площадь поршня.
Полную работу, совершаемую газом, при изменении его от V1 до V2 найдем проинтегрировав
Данное выражение справедливо при любых изменениях объёмов жидких, газообразных. Работу совершённого газа также можно изобразить графически.
То есть работа совершённая газом определяется площадью заштрихованной фигуры.
Вопрос. Теплоемкость. Различают удельную и молярную теплоемкость.
Удельная теплоемкость показывает какое количество теплоты необходимо для нагревания одного килограмма вещества на один кельвин.
Различают также теплоемкости при постоянном объеме и при постоянном давлении когда процессе нагревания эти параметры остаются переменными (P=const V=const) Первое начало термодинамики для одного моля газа с учетом молярной теплоемкости.
Если газ нагревают при постоянном объеме то работа внешних сил равна 0 и сообщаемая газу теплота идет только на увеличение внутренней энергии.
Молярная теплоемкость при изохорном процессе. Если газ нагревается при постоянном давлении то первое начало термодинамики в виде.
Учитывая что что при нагревании газа P=const требуется дополнительное количество теплоты на совершение работы, так как постоянство давления обеспечивается увеличением объема. Выражение для Отношение
Вопрос. Изобарный процесс. Изобарный процесс подчиняется закону Гей-Люссака. См вопрос №2 При изобарном процессе газом совершается работа на увеличение объема.
Используя уравнение Клаперона-Менделеева для выбранных двух произвольных состояний
В изобарном процессе газу сообщается количество теплоты
Вопрос. Изохорный процесс. Подчиняется закону Гей-Люссака. (См вопрос №2) При изохорном процессе газ не совершает роботы над внешними силами. Вопрос. Адиабатный процесс. Это процесс без теплообмена с окружающей средой то есть Q=0
Графически адиабатный процесс для наглядности изображают с изотермическим процессом. Адиабатный процесс подчиняется уравнение Пуассона. Рассмотренные процессы имеют общею особенность они происходят при постоянной теплоемкости в изохорном и изобарном это
Вопрос. Энтропия. Для выяснения физического содержания этого понятия рассматривают отношение теплоты Q полученной телом в изотермическом процессе к температуре К теплоотдающего тела называемая приведенным количеством теплоты Найдем изменение энтропии в разных процессах идеального газа так как или Вопрос. Цикл Карно. Основываясь на второе начало термодинамики Карно вывел следующие теорему из все периодических действующих тепловых машин имеющих одинаковую температуры нагревателей Т1 и холодильников Т2 наибольшим КПД обладают обратимые машины при этом КПД машин работающих при одинаковых температурах Т1 и Т2 равны друг другу и не зависят от природы рабочего тела а определяются только температурами. Карно проанализировал цикл состоящий из двух изотерм и двух адиабат.
Изотермическое расширение и сжатие 1-2, 3-4. А адиабатное расширение 2-3, 4-1. При изотермическом расширении U=const и количество теплоты получаемым газом Q1= работе расширения.
Вопрос 25. Смачивание. Капля воды растекаясь по стеклу принимает форму изображенную на рисунке А а капля ртути имеет другую форму рисунок Б.
В первом случаи говорят что жидкость смачивает твердую поверхность а во втором не смачивает ее. Смачивание зависит от характера сил действующих между молекулами поверхностных слоев соприкасающихся сред для смачивающейся жидкости силы притяжения между молекулами жидкости и твердого тела больше чем между молекулами самой жидкости и жидкость стремится увеличить площадь соприкосновения для не смачиваемой жидкости сила притяжения между молекулами жидкости и твердого тела меньше чем между молекулами жидкости и жидкость стремится уменьшить поверхность соприкосновения. В точке О приложены три силы поверхностного натяжения. Угол
Краевой угол может быть как острым (рис А) так и тупым (рис Б). Если Вопрос. Твердые тела.
Твердые тела характеризуются наличием значительных сил межмолекулярного взаимодействия сохраняет не только свой объем но и форму. Твердые тела или кристаллы имеют правильную геометрическую форму что является результатом упорядоченного расположением частиц (атомов, молекул, ионов) составляющих кристалл. Структура для которой характерно регулярное расположение частиц с периодической повторяемостью в трех измерениях называется кристаллической решеткой. Точки в которых расположены частицы а точнее средние равновесные положения около которых частицы совершают колебания называются узлами кристаллической решетки. Кристаллические тела можно разделить на две группы монокристаллы и поликристаллы. Монокристаллы это твердые тела частицы которых образуют единую кристаллическую решетку, встречаются редко, примерами могут служить соль, лед. В настоящее время в основном выращиваются искусственно. Большинство твердых тел состоят из беспорядочно ориентированных мелких кристаллических зерен, это поликристаллы (металлы, их сплавы, горные породы). Существует два признака для классификации кристаллов: 1) Кристалло-графический 2) Физический В первом случае важна только пространственная периодичность в расположении частиц. По физическому признаку кристаллы делятся на четыре группы: 1) Ионные кристаллы - в узлах кристаллической решетки располагаются поочередно ионы противоположного знака. Ионными кристаллами являются например натрий хлор и т.д. Связь между ионами то есть силы взаимодействия носят кулоновский (электростатический) характер. 2) Атомные кристаллы – в узлах кристаллической решетки располагаются нейтральные атомы удерживающиеся в узлах ковалентными связями, например алмаз, графит, кремний, германий и т.д. Валентные связи осуществляются парами электронов движущихся по орбитам охватывающих оба атома. Ковалентные силы направлены от центрального атома к вершинам тетраэдра 3) Металлические кристаллы – в узлах решетки располагаются положительные ионы металлов, валентные электроны слабо связаны с атомами и принадлежат не одному атому, а всему кристаллу. Натрий, калий и т.д. 4) Молекулярные кристаллы – в узлах располагаются нейтральные молекулы вещества, силы взаимодействия называются Вандервальсовыми. Примерами могут служить инертные газы: неон, аргон; органические: спирт, парафин, резина. Так как Ваандервальсовые силы довольно слабые, то молекулярные кристаллы легко деформируются. вопрос. Параметры идеального газа. Идеальный газ - идеализированная модель, в которой считают, что: - собственный объем молекул пренебрежительно мал по сравнению с объемом сосуда. - между молекулами газа отсутствуют силы взаимодействия. - столкновение молекул газа между собой и стенками сосуда абсолютно упругие.
Термодинамическая температура. T - Измеряется в кельвинах.
V-объём [м3] Например
M[кг/моль] Водород
Гелий Азот Воздух Кислород Аргон Ar
Удельный объем это объем единицы массы; это величина обратная плотности.
Термодинамическая система это совокупность макроскопических тел которые взаимодействуют и обмениваются энергией как между собой так и с окружающими телами. Состояние системы задается термодинамическими параметрами.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 516; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.151.231 (0.065 с.) |




 .
. =m/M[моль]
=m/M[моль]



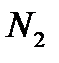






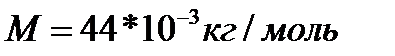

 - Закон Бойля-Мариотта: Для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная.
- Закон Бойля-Мариотта: Для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная. и
и 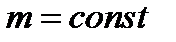
 и
и  Данному закону подчиняется изобарный, т. е. процесс, протекающий при постоянном давлении.
Данному закону подчиняется изобарный, т. е. процесс, протекающий при постоянном давлении.


 и
и  . Данному закону подчиняется изохорный процесс, то есть процесс, протекающий при постоянном объёме.
. Данному закону подчиняется изохорный процесс, то есть процесс, протекающий при постоянном объёме.




 .
.

 .
. 1.
1. 




 Если газ расширяясь передвигает поршень на малое расстояние то он производен над ним работу
Если газ расширяясь передвигает поршень на малое расстояние то он производен над ним работу ,
,
 .
.

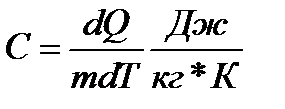



 Согласно формуле
Согласно формуле 

 не зависит от вида процесса определяется лишь температурой и всегда равна
не зависит от вида процесса определяется лишь температурой и всегда равна  . А также дифференцировав уравнение Клаперона-Менделеева
. А также дифференцировав уравнение Клаперона-Менделеева  получим
получим  данное выражение называется уравнением Майера и показывает что
данное выражение называется уравнением Майера и показывает что  на газовую постоянную (для молярной теплоёмкости). Это объясняется тем
на газовую постоянную (для молярной теплоёмкости). Это объясняется тем можно представить в виде
можно представить в виде 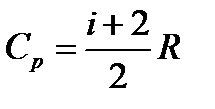 . Удельные теплоемкости.
. Удельные теплоемкости.  .
. называется показателем а
называется показателем а  адиабаты.
адиабаты.
 .
.
 .
. первое начало термодинамики.
первое начало термодинамики. . Первое начало термодинамики для данного процесса имеет вид
. Первое начало термодинамики для данного процесса имеет вид  то есть вся теплота сообщаемая газу идет на увеличение его внутренней энергии
то есть вся теплота сообщаемая газу идет на увеличение его внутренней энергии  . Для произвольной массы газа
. Для произвольной массы газа  .
.

 ,
,  ,
,  . Где
. Где  показатель адиабаты. Вычислим работу совершаемую газом в адиабатном процессе
показатель адиабаты. Вычислим работу совершаемую газом в адиабатном процессе 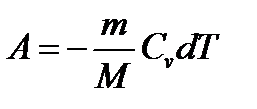 если газ расширяется, от объема
если газ расширяется, от объема  то его температура уменьшается от
то его температура уменьшается от 
 применяя для работы уравнение Пуассона формулу можно преобразовать в виде
применяя для работы уравнение Пуассона формулу можно преобразовать в виде  .
. в изотермическом теплоемкость =
в изотермическом теплоемкость =  бесконечность в адиабатном =0. Процесс в котором теплоемкость остается постоянном называется политропным исходя из первого начало термодинамики при условии постоянства С=const можно вывести уравнение политропы
бесконечность в адиабатном =0. Процесс в котором теплоемкость остается постоянном называется политропным исходя из первого начало термодинамики при условии постоянства С=const можно вывести уравнение политропы где n показатель политропы. При С=0 то
где n показатель политропы. При С=0 то  . При
. При  то
то  . При
. При  . При
. При  .
. . Приведенное количество теплоты сообщаемое телу в любом обратимом круговом процессе
. Приведенное количество теплоты сообщаемое телу в любом обратимом круговом процессе  из равенства 0 интеграла следует что под интегральное выражение есть полный дифференциал некоторой функции которая определяется только состоянием системы и не зависит от пути которым система пришла в это состояние обозначается она
из равенства 0 интеграла следует что под интегральное выражение есть полный дифференциал некоторой функции которая определяется только состоянием системы и не зависит от пути которым система пришла в это состояние обозначается она  функция состояния
функция состояния  называется энтропией. Для обратимых процессов изменение энтропии
называется энтропией. Для обратимых процессов изменение энтропии  для необратимых энтропия возрастает
для необратимых энтропия возрастает  . Последние выражения относится только к замкнутым системам если система обменивается теплотой с внешней средой то ее энтропия может вести себя любым образом. Изменение энтропии можно представить в ввиду неравенства Клаузиуса. Если система совершает переход из состояния 1 в состояние 2 то изменение энтропии
. Последние выражения относится только к замкнутым системам если система обменивается теплотой с внешней средой то ее энтропия может вести себя любым образом. Изменение энтропии можно представить в ввиду неравенства Клаузиуса. Если система совершает переход из состояния 1 в состояние 2 то изменение энтропии  . Физический смысл имеет не сома энтропия а разность.
. Физический смысл имеет не сома энтропия а разность.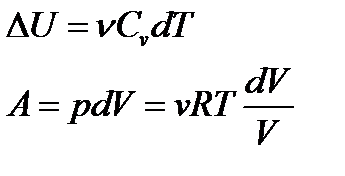 тогда изменение энтропии
тогда изменение энтропии 
 то есть изменение энтропии при переходе идеального газа из состояния 1 в состояние 2 не зависит от вида процесса. Для адиабатного процесса Q=0 тогда
то есть изменение энтропии при переходе идеального газа из состояния 1 в состояние 2 не зависит от вида процесса. Для адиабатного процесса Q=0 тогда  =0 а значит энтропия для данного процесса величина постоянная. Адиабатный процесс называют изоэнтропийным. Из последнего выражения следует что при изотермическом процессе (Т1=Т2)
=0 а значит энтропия для данного процесса величина постоянная. Адиабатный процесс называют изоэнтропийным. Из последнего выражения следует что при изотермическом процессе (Т1=Т2)  . Для изохорного процесса (V2=V1)
. Для изохорного процесса (V2=V1)  .
.
 . При адиабатном расширении отсутствует тепло обмен а работа расширения совершается за счет изменения внутренней энергии
. При адиабатном расширении отсутствует тепло обмен а работа расширения совершается за счет изменения внутренней энергии  . Количество теплоты отданная газом при изотермическом сжатии равно работе сжатия
. Количество теплоты отданная газом при изотермическом сжатии равно работе сжатия  . Работа адиабатного сжатия
. Работа адиабатного сжатия  . Работа совершаемая в результате кругового процесса
. Работа совершаемая в результате кругового процесса  . КПД цикла
. КПД цикла 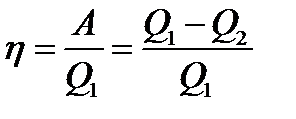 . Применив уравнение Пуассона КПД цикла Карно
. Применив уравнение Пуассона КПД цикла Карно  . То есть определяется температурами нагревателя и холодильника.
. То есть определяется температурами нагревателя и холодильника.
 между касательными к поверхности жидкости и твердого тела называется краевым углом. Условие равновесие капли является равенство нулю суммой проекции сил поверхностного натяжения на направление касательной к поверхности твердого тела.
между касательными к поверхности жидкости и твердого тела называется краевым углом. Условие равновесие капли является равенство нулю суммой проекции сил поверхностного натяжения на направление касательной к поверхности твердого тела.

 больше чем сумма двух других то жидкость растыкается по поверхности твердого тела покрывая его тонкой пленкой тогда имеет место полное смачивание. Если
больше чем сумма двух других то жидкость растыкается по поверхности твердого тела покрывая его тонкой пленкой тогда имеет место полное смачивание. Если  больше суммы двух других то жидкость стягивается в шаровую каплю имея лишь одну точку соприкосновения то имеет место полное не смачивание. В первом случае
больше суммы двух других то жидкость стягивается в шаровую каплю имея лишь одну точку соприкосновения то имеет место полное не смачивание. В первом случае  =0 например керосин на стекле. Во втором случае
=0 например керосин на стекле. Во втором случае  например вода на парафине.
например вода на парафине.


