
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Релятивистское обобщение модели Бора.Содержание книги
Поиск на нашем сайте
Выше мы уже обращали внимание на то, что в тяжелых водородоподобных системах (Z >> 1) электрон становится релятивистским, т.е. нашей модели уже недостаточно. Рассмотрим теперь релятивистское обобщение модели Бора. Так же как и раньше, ограничимся случаем круговых орбит. Запишем релятивистское уравнение движения в виде
Поскольку на круговой орбите модуль вектора скорости остается постоянным, уравнение (4.29) можно переписать в виде
Здесь отличается от нерелятивистского случая (15.11) появлением множителя γ. Будем также считать, квантовое условие Бора (15.12) верно и при релятивистских скоростях. Тогда имеем:
Опять имеем два уравнения (15.31) и (15.30) для определения радиусов орбит и соответствующим им скоростей движения. После несложных преобразований получаем
Отметим, в частности, что выражения для скорости движения по орбите, полученные в релятивистском и нерелятивистском случаях, совпадают. Найдем теперь энергию электрона на орбите. Поскольку при движении в кулоновском поле
получим
Может быть, наиболее удивительным является то, что решение задачи существует не для любых Z. Как видно из (15.33) и (15.35) для основного состояния системы (n = 1) полученные выражения теряют смысл для сверхтяжелых ядер с зарядом больше некоторого критического Z *: Z>Z*=1/ (15.36) При Z = Z * = 137 полная энергия электрона (включая энергию покоя) обращается в ноль, а орбита имеет нулевой радиус. Для ядер с большим зарядом устойчивой орбиты, соответствующей случаю n = 1, в рамках модели Бора найти нельзя. То есть модель Бора фактически предсказывает существование конца таблицы Менделеева. Интересно, что точно такой же ответ получается и в рамках релятивистской квантовой теории, базирующейся на решении волнового уравнения Дирака17. Проверить сделанные предсказания напрямую вряд ли возможно, поскольку синтезировать ядра со столь большим значением Z (необходимо еще электронную оболочку создать) в настоящее время проблематично. Чуть более подробно остановимся теперь на случае небольших значений Z и рассмотрим вопрос о релятивистских поправках к энергетическим уровням атома водорода и водородоподобных ионов. Отметим, прежде всего, что в выражение (3.48) включена также энергия покоя электрона, которую мы не учитывали в рамках нерелятивистской теории. Поэтому для сравнения результатов и нахождения релятивистских поправок перепишем выражение (15.35), исключив из него энергию покоя
s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz-cs w:val="24"/></w:rPr><m:t>)</m:t></m:r></m:e></m:rad></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> Проводя в (15.37) разложение корня в ряд Тейлора, получаем
что, как нетрудно видеть, совпадает с выражением (15.22). Релятивистская поправка к энергии δ Ep получается при учете второго члена разложения корня в (15.37):
Например, для основного состояния атома водорода имеем
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.168.176 (0.009 с.) |

 (15.29)
(15.29) (15.30)
(15.30) - релятивистский фактор. Фактически уравнение движения (15.30)
- релятивистский фактор. Фактически уравнение движения (15.30) (15.31)
(15.31) (15.32)
(15.32) (15.33)
(15.33) (15.34)
(15.34)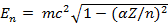 (15.35)
(15.35) =137
=137 (15.37)
(15.37)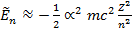 (15.38)
(15.38) (15.39)
(15.39)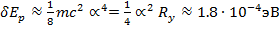 (15.40)
(15.40)


