
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 5. Регресивні моделі з однією вхідною змінноюСодержание книги
Поиск на нашем сайте
Основні поняття Технологічні процеси сільськогосподарського виробництва, особливо процеси механізації, дуже складні за своєю природою. До сих пір відсутні прийняті всіма аналітичні моделі, точно описують закономірності процесів обробки ґрунту, посіву, внесення добрив, збирання сільськогосподарських культур, очищення насіння і т. д. Тому в технологічних процесах сільськогосподарського виробництва дуже часто використовують моделі, які ми раніше визначили як емпіричні. Емпіричні моделі об’єктів і процесів є результатом обробки експериментальних даних про поведінку об’єкта або процесу методами математичного статистичного аналізу. Дуже часто для побудови моделей об’єктів за результатами експериментальних досліджень використовують математичний апарат регресійного і кореляційного аналізу. Терміни «регресія» і «кореляція» були введені в широкий ужиток статистиками Ф. Гальтон і К. Пірсоном в кінці XIX в. Вони вивчали взаємозалежності зростання і маси людей різного віку і зіткнулися з необхідністю введення таких показників зазначеної залежності, які б відображали зв’язок між досліджуваними характеристиками людини, але не визначали б один одного строго однозначно. В даний час «регресія» і «кореляція» - основні поняття статистики. Регресія (лат. regressio - зворотний рух, відхід) в теорії ймовірностей і математичній статистиці - залежність середнього значення якої-небудь величини від деякої іншої величини або від декількох величин. Кореляція (від лат. correlatio «співвідношення, взаємозв’язок») або кореляційний залежність - це статистичний взаємозв’язок двох або більше випадкових величин (або величин, які можна з деякою допустимої ступенем точності вважати такими). При цьому зміни значень однієї або декількох з цих величин супроводжують систематичні зміни значень іншої або інших величин. Основне завдання кореляційного аналізу - виявлення значущості зв’язку між значеннями різних випадкових величин. Залежність між величинами (в тому числі і випадковими), при яких одному значенню однієї величини (аргументу) відповідає одне або кілька цілком певних значень іншої величини, називається, відповідно, однозначною або багатозначною функціональною залежністю [11]. Залежність між величинами, при якій кожному значенню однієї величини відповідає з відповідною ймовірністю безліч можливих значень іншої, називають ймовірнісної (стохастичною, статистичної). Прикладами кореляційної зв’язку є залежності між нормами внесення добрив та врожайністю, між глибиною обробки ґрунту та витратами палива, між температурою та вологістю матеріалу і т. д.
Математичний апарат регресійного аналізу дозволяє: ● оцінити невідомі параметри пропонованої до дослідження регресійній моделі; ● перевірити статистичну значущість параметрів моделі; ● перевірити адекватність моделі; ● оцінити точність моделі. Вид регресійній моделі пропонує сам дослідник, при цьому він виходить з наступного: ● фізичної сутності досліджуваного об’єкта або явища; ● характеру експериментального матеріалу; ● аналізу апріорної інформації. Найпростішим для моделювання є об’єкт, у якого один вхідний і один вихідний фактор (рис. 5.1). Вхідний фактор характеризує вплив на досліджуваний об’єкт. У технологічних процесах сільськогосподарського виробництва це можуть бути температура, сила, час, геометричні параметри робочих органів, характеристики оброблюваного матеріалу і т. д. Вихідний фактор характеризує реакцію (відгук) об’єкта на вплив вхідного фактора. Вихідні фактори в технологічних процесах сільськогосподарського виробництва – продуктивність агрегату, якість виконання операції, величина зносу матеріалу і т. д.
Рис. 5.1. Об’єкт дослідження з одним вхідним і одним вихідним фактором
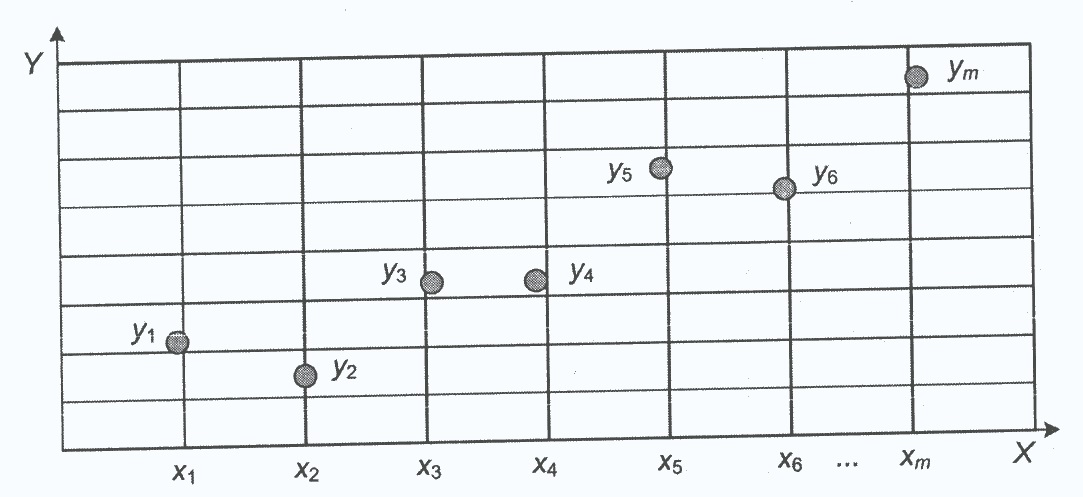
Для початку побудови емпіричної моделі необхідно мати дані експериментальних досліджень об’єкта (у вигляді таблиці або графіка), в яких кожному значенню вхідного фактора (X) відповідає значення вихідного чинника (Y), тобто відома пара чисел (x, y). Пари випадкових змінних (x, y) підкоряються деякого двовимірного ймовірнісному розподілу. Загальна кількість пар чисел нехай одно m (рис. 5.2).
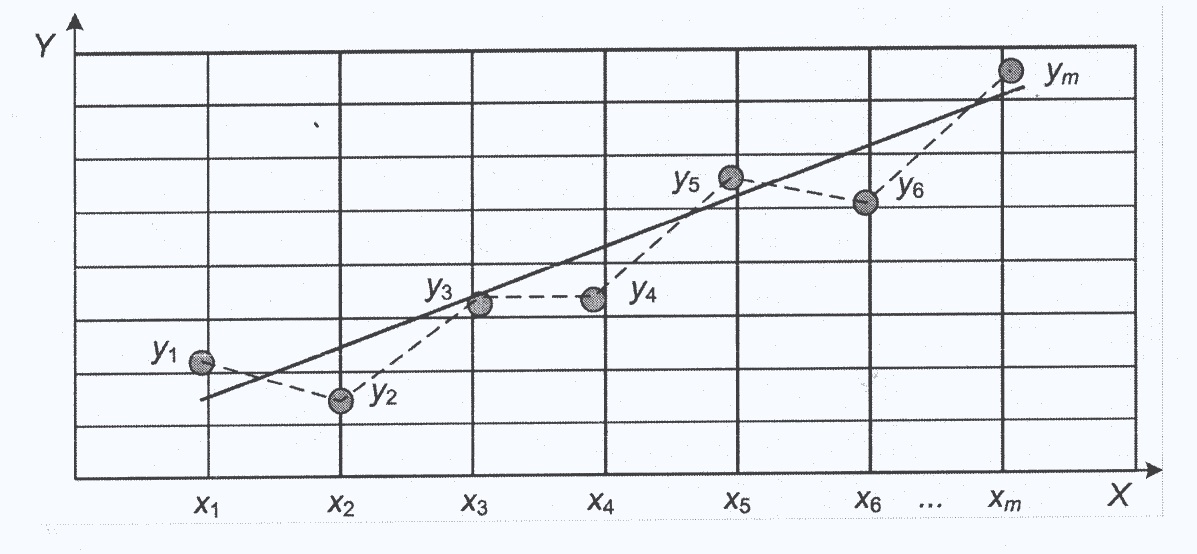
Рис. 5.2. Графічне відображення результатів експерименту Даний графік називається діаграмою розсіювання, або точкової діаграмою [12]. Необхідно знайти таку криву, яка б найкращим чином апроксимувати експериментальні точки. Для зручності подальшого дослідження об’єкта ця крива повинна мати для свого опису одну єдину формулу (функцію). Якщо ми з’єднаємо точки на графіку, то отримаємо ламану лінію, що складається з декількох прямих відрізків і описувану відповідною кількістю лінійних моделей. Це вкрай незручно для дослідження. Необхідно знайти криву, найкращим чином описує всі експериментальні точки (рис. 5.3). Таку криву називають кривою регресії, або регресійній кривої Y по X. У загальному випадку крива регресії може мати будь-який вид (монотонно зростаюча монотонно спадна, з точками перегину і т. д.), Але вона повинна бути безперервною, тобто не повинна мати розривів. У найпростішому випадку крива регресії має вигляд прямої лінії.
Рис. 5.3. Побудова лінії регресії Зазвичай побудова моделей і дослідження об’єкта починають з найпростіших моделей - лінійних. Лінійної моделі відповідає крива регресії у вигляді простої лінії. Як видно з графіка (див. рис. 5.3), завжди є відхилення експериментальних точок від кривої регресії, що викликано впливом інших (неврахованих в моделі) зовнішніх факторів на досліджуваний об’єкт. У моделюванні вихідний фактор ще називають залежною вихідної змінної, а вхідний - незалежної вхідної змінної. Під час дослідження об’єкта вхідний фактор завжди носить детермінований характер, а вихідний - випадковий. Вираз, який встановлює зв’язок між випадковою залежною і детермінованою незалежної змінними, являє собою рівняння регресії. Термін «рівняння регресії», строго кажучи, не зовсім коректний [12], але загальноприйнятий. Модель, побудована на основі рівняння регресії, є регресійної моделлю. Як зазначалося раніше, для отримання регресійних моделей (рівнянь регресії) використовується математичний апарат регресійного аналізу. Отже, як ми вже говорили, підбір кривої регресії і регресійній моделі зазвичай починають з простої прямої лінії і, відповідно, з лінійної моделі. Якщо мати необмежено велику кількість експериментальних точок, то лінійна регресійна модель має вигляд [12]:
де ŷ – значення вихідної змінної, розраховані (передбачені) по лінійної моделі; x – значення вхідної змінної; β0 і β1 – коефіцієнти регресії; ε – залишок (нев’язка). Визначення коефіцієнтів регресії здійснюється на основі методу найменших квадратів. Метод найменших квадратів застосовують в тих випадках, коли випадкова варіація вхідного фактора зневажливо мала в порівнянні зі спостережуваним діапазоном його вимірювання [12], тобто значення вхідної змінної вважаються фіксованими. Суть методу в тому, що підбираються такі β0 і β1, при яких сума квадратів відхилень виміряних величин y від передбачених ŷ була б мінімальною. Для пар спостережень можна записати:
Відхилення виміряної величини y від передбачуваної ŷ:
Сума квадратів відхилень виражається у вигляді:
де S – функція суми квадратів. Підберемо b0 і b1 так, щоб при підстановці їх замість β0 і β1 значення S було мінімальним з можливих. Знайдемо приватні похідні (∂):
Найменше значення суми квадратів відхилень досягається в тому випадку, коли коефіцієнти β0 і β1 задовольняють умові[11]:
Наявні експериментальні дані у вигляді пар (хi, yi) є лише обмеженою вибіркою із загального числа станів досліджуваного об’єкта. Тому можна визначити тільки оцінки коефіцієнтів β0 і β1, які позначають, відповідно, b0 і b1:
Такі моделі в літературі називають однофакторними регресійними моделями. Коефіцієнт регресії b1 визначається за формулою [12]:
де хi – значення вхідного фактора під час експерименту; yi – значення вихідного фактора, відповідне xi;
Коефіцієнт регресії b0:
Отримуємо:
де
|
|||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.166.156 (0.012 с.) |


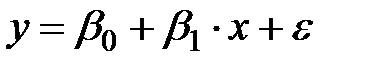 , (5.1)
, (5.1)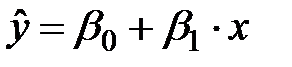 , (5.2)
, (5.2)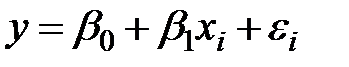 (5.3)
(5.3)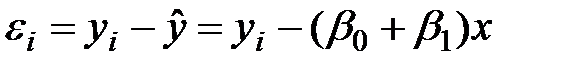 (5.4)
(5.4)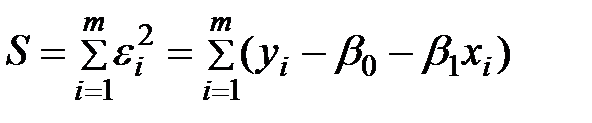 , (5.5)
, (5.5)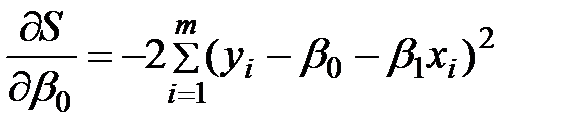 , (5.6)
, (5.6)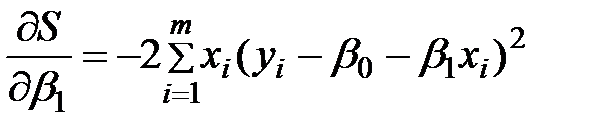 . (5.7)
. (5.7)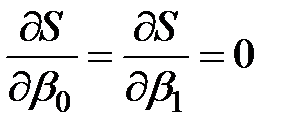 . (5.8)
. (5.8)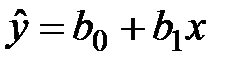 . (5.9)
. (5.9)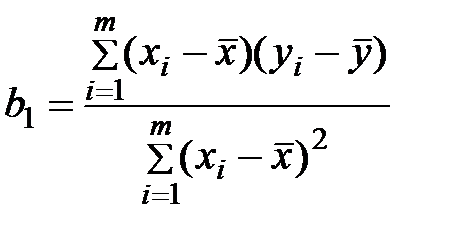 , (5.10)
, (5.10)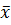 – середнє значення вхідного фактора, що визначається за формулою:
– середнє значення вхідного фактора, що визначається за формулою: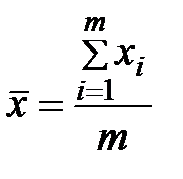 , (5.11)
, (5.11)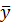 – середнє значення вихідного чинника, що визначається за формулою:
– середнє значення вихідного чинника, що визначається за формулою: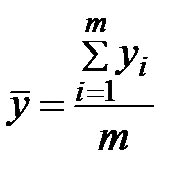 . (5.12)
. (5.12)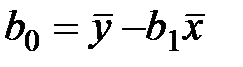 . (5.13)
. (5.13)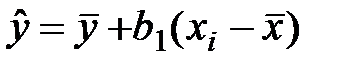 , (5.14)
, (5.14)


