
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет процесса дросселирования ПГСодержание книги
Поиск на нашем сайте
Для т/д-кого расчета пр-са НТС и определения потребного кол-ва ингибитора, следующему предотвращению г/о в промысловых сеп-ных устройствах и регулирующих клапанах на ГРС, необходимо знать t-ру газа после дросселирования. Эту температуру можно определить по известным начальному P1, t1 и конечному давлению P2, зная интегральный или среднедиф-ный эффект Джоуля-Томсона. Осн-м признаком процесса дросселирования явл-ся ровный по теплосодержанию или энтальпии газа до и после дросселирования, независимо от величины изменения Р. Т.е. i1=i2 – энтальпия Поскольку различия скоростей течения газа до и после дросселирования, а также наличие некоторой реальной теплопередачи может вызвать изменение теплосодержания. Если изменение скорости незначительно, либо равно 0, а величина реальной теплопередачи невелика и ею можно пренебречь, то можно принять ¶i=0. Когда, при дросселировании газа давление уменьшают на значительную величину, то эффект Джоуля-Томсона называют интегральным. Дифференциальный эффект Джоуля-Томсона это изменение температуры, происходящее от бесконечно малого изменения давления mi=(¶T/¶P)i=const (1) mi – дифференциальный эффект Джоуля-Томсона в промысловой практике в основном всегда имеет конечный перепад давления газа, поэтому диф. Эффектом обычно считается некоторый конечный перепад давления газа и (Dp=0,1 МПа). Свяжем (1) с 3-м параметром состояния – объемом. Для этого воспользуемся третьим законом т/д-ки: dQ=di–V×dP (2) Q – кол-во тепла; V – объем системы; Если процесс протекает при постоянном давлении, то изменение кол-ва тепла системы будет равно изменению ее теплосодержанию: dQ=di–CpdT (3) Отсюда Cp=(¶i/¶T)p (4) Cp – теплоемкость газа при постоянном давлении. Изотермическое влияние давления на энтальпию: (¶i/¶P)T=V–T(¶V/¶T)P (5) энтальпию любого процесса можно выразить в зависимости от параметров Р и Т: di=(¶i/¶P)Т×dP+(¶i/¶T)P×dT (6) Подставив (6) в (4) и (5): di=Cp×dT+[V–T(¶U/¶T)P]×dP (7) Для рассматриваемого процесса процесса дросселирования, когда di=0 из (7) получим: mi=(dP/¶P)=(T×(dV/dT)P–V)/CP (8) Этим выражением определяется дифференциальным эффектом Дж.-Томп. Через абсолютные параметры состояния газа. Дифференциальный эффект можно вычислить теоретически из уравнения состояния Ван-дер-Ваальса, Битта, Бертло и др. Из уравнения Бертло справедливо для запретной области теиператур и при умеренных давлениях (до 10 Мпа) можно получить формулу диф. дроссель эффекта в виде: mi=9×A×R×Tк×[1–8×(Тк/Т1)2]/(128×Рк×Ср) (9) где Tк, Рк – критическая температура и давление газа. Т1 – начальная тем-ра газа. СР – молярная теплоемкость газа при постоянном давлении. Преобразуя (8) к виду удобному для вычисления диф. дроссель эффекта, выразив его через остаточный объем а=R×T/P–V (10) Продифференцируем 10 по Т при Р=соnst. И результат дифференцирования подставив в уравнение (8), после преобразований для коэффициента Джоуля-Томпсона mi=[a–T×(¶a/¶T)P]/CP (11) выражая (11) через приведенные параметры газа t, p, и a получим, что mi=aк×[aпр–t×(¶aпр/¶t)p]/СР (12) где СР=СРо+DСP (13) СРо – молярная теплоемкость идеального газа при атмосферном давлении; DСР – изотермическая поправка теплоемкости на давление. Остаточный критический объем: aк=Р×Тк/Рк–Vк (14) p=Р/Рк (15), t=Т/Тк (16) aпр=a/aпр (17) Соответсвенно при Р, Т и остат. объемы. Расчеты показывают, что величина Ркр×aпр/Ткр для у/в-ых газов колеблется в пределах 1,41…1,47 и в среднем можно принять Рк×aк/Тк=1,44 (18) Отсюда aк=1,44×Тк/Рк (19) С учетом (13), (19) уравнение (12) для коэффициента Дж.-Томпсона: mi=1,44×(Тк/Рк)×[aпр–t(¶aпр/¶t)p]/(Сро+DСР) (20) Преобразуем (20) в форму Рк×mi×Cp/Тк=1,44×[aпр–t(¶aпр/¶t)p] (21) Рк×mi×Cp/Тк – обобщенная ф-ция Дж.-Томпсона. Величина ее, вычисленная по (21) приведена на рисунке 1 в зависимости от p и t. Из ур. (20) получим окончательное выражение для вычисления коэф. Дж.-Томсона для ПГ: mi=(Тк/Рк)×[Рк×mi×Cp/Tк]/(Сро+DСР) (22) По (22) можно вычислить коэффициент Дж.-Томсона при этом обобщенная функция Рк×mi×Cp/Tк в зав-ти от прив. параметров определяется по графику рис. 1. Среднее отклонение, вычисленных по нашему методу коэффициентов Дж.-Томсона. для чистых компонентов и смесей от опытных данных составляют 7 %. При пост. Р-х и t-рах коэф. Дж.-Томсона. для сухого у/в-го газа имеет большую величину для газа с большой молекулярной массой. При промысловых расчетах, связанных с дросселированием газа, обычно пользуются интегральным дроссель-эффектом, который определяется как произведение средних значений: дифференциального дроссель-эффекта на изменение давления. Для аналитического определения дроссель эффекта при изменении давления от Р1 до Р2, необходимо проинтегрировать величину:
Для газа, подчиняющегося уравнению Ван-дер-Ваальса, Чарный получил из (23) след. Выражение Т1–Т2+2×а×ln[(2×a–T1)/(2×a–T2)]=A×b×(P1–P2)/CP (24) где Т1, Т2 – начальная и конечная температура газа; Р1, Р2 – начальное и конечное давления газа; СР – уд. теплоемкость газа. a=27×R2×Tкр2/(64×Ркр) (25) b=R×Tк/(8×Рк) (26) (26) можно преобразовать к виду для расчета интегрального дроссель эффекта. DТ=Т1–Т2=А×R×Tк/(8×СР)(1/t¢1–1)×(p1–p2) (27) где: p¢1=p¢/Тинв (28) p1=Р1/Ркр (29) p2=Р2/Ркр (30) Тинв=27/(4×Ткр) (31) формулу 27 можно преобразовать к след виду: DТ=5,569×(1/t¢1–1)(p1–p2) (32) анные, полученные по (27) и (32) совпадают с экспериментальными, и данными. (32) можно использовать для расчета интегрального эффекта ПГ с содержанием газа >90 %. Уменьшение температуры природного газа при данном изменении еа штуцере и известном давлении газа можно определить по рис. 2. При интегральных расчетах температуру газа в процессе дросселирования можно определить энтальпийным диаграммам, т.е. диаграмма состояния, которые для каждого индивидуального компонента газа строятся экспериментальным данным. Чаще всего параметры процесса дросселирования определяются по диаграммам состояния для чистого газа. По этим диаграммам получают приближенные значения величины интегрального дроссель эффекта, применительно к природному газу. В реальных условиях интегральный дроссель эффект для ПГ, определено для СН4. Эти отклонения могут быть вызваны отклонением в составе, присутствием в газе азота и СО2, а также наличие капельной жидкости Н2О и у/в-ого конденсата, который способствует увеличению конечной температуры газа, т.е. уменьшению дроссель эффекта. Рядом исследователей построены номограммы, позволяющие определить температуру ПГ после дросселирования. Одна из таких номограмм построена Будаяном, на основе диаграммы i – lgP для метана приведена на рис. 3. Данная номограмма позволяет определить интегральный дроссель эффект метана нужной для практики газовой промышленности области Р=0…32 МПа и Т=70…120оС. Эта номограмма с достаточной точностью можно пользоваться для определения дроссель эффекта, или температуры после дросселирования ПГ, с содержанием метана >90% рис. 3.
|
||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.199 (0.008 с.) |

 и предение параметрах газа обобщенных функциях. Т.к. остаточный объем есть разность м/у объемами ид. И реального газов, то:
и предение параметрах газа обобщенных функциях. Т.к. остаточный объем есть разность м/у объемами ид. И реального газов, то: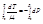 (23)
(23)


