
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимодействие акустического поля с веществомСодержание книги
Поиск на нашем сайте
Взаимодействие акустического поля (акустических волн) с веществом лежит в основе различных методов неразрушающего контроля, например теневого метода, эхометода и других, а также измерений различных физических величин, например толщины изделий и покрытий. 2.4.1. Общие сведения об акустических волнах Акустическим полем называют область пространства, упругие колебания в точках которого определяются их положением относительно объекта, порождающего это поле: излучателя отражателя, границы раздела сред и т. д. [18]. Упругие колебания – это колебания механических систем, упругой среды или ее части, возникающие под действием механического возмущения. Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с некоторой скоростью υ. Процесс распространения колебаний в пространстве называется волной. Частным случаем упругих или акустических волн является человеческий звук. Колебательный процесс частиц может быть описан уравнением
где В зависимости от частоты упругие колебания и волны разделяют на инфразвуковые (до 16 Гц), звуковые, слышимые ухом человека (от 16 Гц до 20 кГц), ультразвуковые (более 20 кГц), гиперзвуковые (более 109 Гц). Упругие колебания и акустические волны, особенно ультразвукового диапазона, широко используются в технике. Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Упругие поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн. Продольные волны иначе называются волнами сжатия-растяжения (l –волны). Поперечные волны иначе называются волнами сдвига (t –волны).
В зависимости от вида поляризации сдвиговые волны разделяются на плоскополяризованные и волны с элептической и круговой поляризацией. Кроме объемных продольных и поперечных волн в упругой среде могут также распространяться поверхностные волны (s–волны) – упругие волны, распространяющиеся вдоль поверхностной, слабо напряженной границы твердого тела. Разновидностью поверхностных волн являются волны Рэлея (R–волны), которые распространяются на границе «твердая среда – газ». Поверхностные волны Рэлея являются комбинацией продольных и поперечных волн. При этом частицы их совершают колебания в приповерхностном слое по эллиптическим орбитам. Волны Рэлея чувствительны к состоянию поверхности (шероховатости, покрытиям, загрязнениям поверхности и др.) и затухают на глубине 2.4.2. Основные параметры акустических волн Для характеристики акустических волн можно выделить несколько основных параметров, к которым относятся: скорость распространения С, м/c, колебательная скорость частиц среды V, м/c; давление в волне Р, Н/м2; интенсивность волны J, Вт/м2; частота f, Гц; длина волны, м. Скорость распространения упругой волны в среде характеризует скорость распространения определенного состояния среды (например, зоны сжатия), зависит от характеристик этой среды и для плоских продольной, поперечной и поверхностных волн определяется из соотношений [8]
где Сl, Сt и СR – скорости продольной, поперечной и поверхностной волн; Скорость распространения зависит от свойств упругой среды. Например, в углеродистой стали (ρ = 7,8.103 кг/м3) Сl = 5 850 м/с, Сt = 3 230 м/с, а в меди Колебательная скорость характеризует скорость распространения механического движения частиц в процессе их смещения относительно положения равновесия:
Давление в волне Р определяется как
где Z – акустический импеданс среды. Акустический импеданс – это отношение комплексного звукового давления к объемной колебательной скорости [18]. При распространении акустических волн в протяженных средах используется понятие удельного акустического импеданса, равного отношению звукового давления к колебательной скорости. Акустический импеданс характеризует среду, в которой распространяется волна, и называется волновым сопротивлением среды. Если среда имеет большое значение Z, то она называется «жесткой» (акустически твердой). В таких средах даже при высоких давлениях колебательные скорости малы. Среды, в которых даже при малых давлениях достигаются значительные колебательные скорости и смещения, получили названия «мягких» (податливых). Интенсивность волны – количество энергии, перенесенное волной за 1 с через поперечное сечение площадью 1 м2, расположенное под углом φ. Для плоской волны
Очень часто для оценки интенсивности волн используются не абсолютные величины, а относительные, например отношение величин на входе и выходе системы, причем обычно используется логарифм этого отношения. 2.4.3. Распространение акустических волн в среде При распространении плоской акустической волны в среде в результате взаимодействия со средой происходит ее затухание, т. е. интенсивность, амплитуда колебаний, давление волны уменьшаются. Затухание определяется физико-механическими свойствами среды, типом волны, геометрическим расхождением лучей и происходит по экспоненциальному закону, например, для амплитуды можно записать
где х – расстояние, пройденное волной; Чем больше расстояние, тем сильнее ослабляется акустическая волна. Амплитуда колебаний и звуковое давление ультразвуковой волны снижаются в Величина, обратная коэффициенту затухания, показывает, на каком пути амплитуда волны уменьшается в е раз. Коэффициент затухания складывается из коэффициентов поглощения δП и рассеяния
При поглощении акустическая энергия переходит в тепловую, а при рассеянии уходит из направления распространения волны. Основными факторами, обусловливающими поглощение энергии, являются: вязкость, упругий гистерезис и теплопроводность. Рассеяние происходит из-за наличия в среде неоднородностей (с отличным от среды волновым сопротивлением), размеры которых соизмеримы с длиной волны. Процесс рассеяния зависит от соотношения длины волны и среднего размера неоднородности. Чем крупнее структура, тем больше рассеяние волны. В газах и жидкостях затухание акустической волны определяется поглощением, рассеяние отсутствует. Коэффициент поглощения пропорционален квадрату частоты. В качестве характеристики поглощения звука в этих средах вводят параметр
В металлах, так как они имеют зернистую структуру, затухание акустических волн обусловлено рефракцией и рассеянием. Под рефракцией понимают непрерывное отклонение акустической волны от прямолинейного направления распространения. Коэффициент рассеяния в металлах зависит от соотношения среднего размера неоднородностей (среднего размера зерна
где С 3 – коэффициент, не зависящий от величины зерна и анизотропии; FА – фактор анизотропии. При
где А и В – постоянные. При
На значение коэффициента затухания оказывает влияние температура среды. Для оценки изменения δ при измерении температуры можно использовать формулу
где Δ t = t – t 0; t – температура среды; δ0 – коэффициент затухания при начальной температуре t 0; k δ – температурный коэффициент δ.
При падении продольной волны образуются отраженная и преломленная продольные волны и в результате трансформации – отраженная и преломленная поперечные волны. Подобный процесс наблюдается и при падении поперечной волны. В жидкостях имеется только одна отраженная и одна преломленная волна.
где C i – скорость падающей (продольной или поперечной) волны; Cl 1 и Ct 1 – скорости распространения продольных и поперечных волн в первой среде (I); Cl 2 и Ct 2 – скорости распространения продольных и поперечных волн во второй среде (II). В акустике под углом падения ультразвуковой волны понимают угол, образованный нормалью к границе раздела, проходящего через точку прохождения луча, и направлением распространения пучка. Для продольной волны при некотором значении угла падения β l 1, называемого первым критическим углом
При падении поперечной волны из твердой среды на границу раздела при определенном угле падения Значения критических углов определяются следующим образом. Используя выражение (2.50), можно записать:
Свойства акустических волн широко используются при создании наклонных преобразователей для контроля изделий продольными и поперечными волнами (первой средой при этом является призма из оргстекла, а вторая – контролируемое изделие). При практическом использовании наклонных преобразователей необходимо знать значения критических углов. Например, при падении продольной волны l из оргстекла на границу контролируемого изделия из стали они имеют значения: первый критический угол Прохождение акустической волны из одной среды в другую характеризуется коэффициентом прозрачности D, а отражение – коэффициентом отражения R, которые при падении волны по нормали к границе раздела определяются как
где А0, Апр и Аотр – амплитуды падающей, прошедшей и отраженной волн. Эти коэффициенты можно определить и по другим параметрам [8]: интенсивности J, давлению Р, колебательной скорости V и др.:
где Z1 и Z2 – удельные акустические сопротивления первой и второй среды. Коэффициенты прозрачности и отражения определяются для каждого типа возникающих волн, и их значения зависят от соотношения акустических сопротивлений сред. Например, при Z1 = Z2 наблюдается полное прохождение ультразвука через границу раздела (R = 0; D = 1). Если Z1 >> Z2, то энергия падающей волны полностью отражается (R = 1; D = 0). Явления отражения и прохождения акустической волны широко используются в неразрушающем ультразвуковом контроле различных изделий. Например, на способности ультразвуковых волн, излучаемых в контролируемый объект, отражаться от дефектов с последующей регистрацией эхосигналов основан эхометод акустического контроля. Явление прохождения ультразвуковой волны используется в теневом, зеркально-теневом и других методах акустического неразрушающего контроля.
|
||||||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.24.148 (0.011 с.) |

 , (2.40)
, (2.40)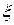 – отклонение колеблющейся частицы от положения своего равновесия;
– отклонение колеблющейся частицы от положения своего равновесия;  – максимальная амплитуда смещения частицы;
– максимальная амплитуда смещения частицы; 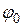 – начальная фаза колебаний.
– начальная фаза колебаний. ;
; 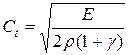 ;
; 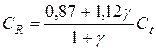 , (2.41)
, (2.41)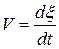 . (2.42)
. (2.42)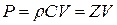 , (2.43)
, (2.43)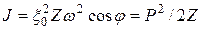 . (2.44)
. (2.44) , (2.45)
, (2.45)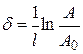 – коэффициент затухания, м-1, иногда эту единицу записывают непер/м (Нп/м). Часто коэффициент затухания выражают в дБ/м.
– коэффициент затухания, м-1, иногда эту единицу записывают непер/м (Нп/м). Часто коэффициент затухания выражают в дБ/м.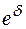 раз на каждую единицу длины пути х, проходимого волной, а интенсивность как энергетическая единица – в
раз на каждую единицу длины пути х, проходимого волной, а интенсивность как энергетическая единица – в  раз.
раз.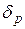 :
: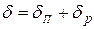 . (2.46)
. (2.46)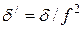 . Рассеяние может отсутствовать и в однородных аморфных материалах типа пластмассы, стекла и т. п. материалах. Затухание ультразвуковых волн зависит от материала среды, в которой они распространяются. Например, в воздухе, в пластмассах и т. п. средах затухание велико. В воде затухание в тысячи раз меньше, в стали – незначительное [8].
. Рассеяние может отсутствовать и в однородных аморфных материалах типа пластмассы, стекла и т. п. материалах. Затухание ультразвуковых волн зависит от материала среды, в которой они распространяются. Например, в воздухе, в пластмассах и т. п. средах затухание велико. В воде затухание в тысячи раз меньше, в стали – незначительное [8].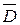 ) и длины волны и может определяться как [8]
) и длины волны и может определяться как [8]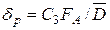 , (2.47)
, (2.47)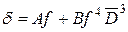 , (2.48)
, (2.48)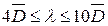 коэффициент рассеяния
коэффициент рассеяния . (2.49)
. (2.49)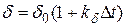 , (2.50)
, (2.50)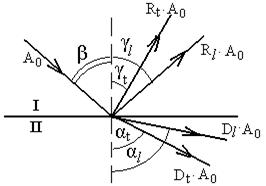 Если на пути распространения волны встречается среда с другими акустическим свойствами, то акустическая волна частично проходит во вторую среду, частично отражается от нее. При этом может происходить трансформация типов волн. Трансформацией называется преобразование волн общего типа в волны другого типа, происходящие на границе раздела двух сред. При нормальном падении ультразвуковых волн (β = 00) трансформации не происходит. В общем случае границы двух твердых тел (рис. 2.12) возникают две (продольная и поперечная) отраженные и две преломленные волны.
Если на пути распространения волны встречается среда с другими акустическим свойствами, то акустическая волна частично проходит во вторую среду, частично отражается от нее. При этом может происходить трансформация типов волн. Трансформацией называется преобразование волн общего типа в волны другого типа, происходящие на границе раздела двух сред. При нормальном падении ультразвуковых волн (β = 00) трансформации не происходит. В общем случае границы двух твердых тел (рис. 2.12) возникают две (продольная и поперечная) отраженные и две преломленные волны. Углы падения β, отражения γ и преломления α связаны между собой. Направления отраженных и преломленных (прошедших) волн определяются законом Снелиуса
Углы падения β, отражения γ и преломления α связаны между собой. Направления отраженных и преломленных (прошедших) волн определяются законом Снелиуса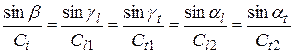 , (2.51)
, (2.51) , преломленная волна не проникает во вторую среду, а распространяется по поверхности. При дальнейшем увеличении угла падения преломленная поперечная волна t 2 также начнет скользить по границе раздела двух сред. Наименьший угол падения, при котором это наблюдается, называется вторым критическим углом
, преломленная волна не проникает во вторую среду, а распространяется по поверхности. При дальнейшем увеличении угла падения преломленная поперечная волна t 2 также начнет скользить по границе раздела двух сред. Наименьший угол падения, при котором это наблюдается, называется вторым критическим углом 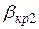 .
. продольная отраженная l 1 волна сольется с поверхностью. Наименьший угол поперечной волны, при котором еще отсутствует отраженная продольная волна, называется третьим критическим углом
продольная отраженная l 1 волна сольется с поверхностью. Наименьший угол поперечной волны, при котором еще отсутствует отраженная продольная волна, называется третьим критическим углом 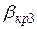 .
.
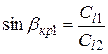 ;
;  ;
; 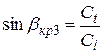 . (2.52)
. (2.52) ;
; 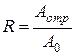 , (2.53)
, (2.53)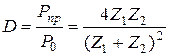 ;
;  , (2.54)
, (2.54)


