Види робіт під час реалізації імітаційної моделі та етапи її складання.

Практична реалізація методу машинної імітації передбачає, що послідовно чи спільно виконуються такі види робіт: 1) Побудову імітаційної моделі, яка має бути представлена у вигляді логічної структурної схеми. 2) Розробку методики імітаційного моделювання, включаючи методику планування експериментів та методику статистичної обробки інформації. 3) Створення програмного забезпечення імітаційного моделювання за допомогою загальноприйнятих засобів програмування чи спеціалізованих мов імітаційного моделювання. 4) Проведення машинної імітації на ЕОМ, аналіз та узагальнення результатів, прийняття рішення щодо можливого уточнення імітаційної моделі. Послідовність складання імітаційної моделі передбачає такі кроки:

1) визначення задачі та її аналіз; 2) визначення вимог до інформації; 3) збирання інформації; 4) висування гіпотез і прийняття припущень; 5) встановлення основного змісту моделі; 6) визначення параметрів, змінних і критеріїв ефективності; 7) опис концептуальної моделі й перевірка її вірогідності; 7) побудова логічної структурної схеми (блок-схеми). На першому етапі моделювання конкретного об’єкта (системи) на ЕОМ необхідно побудувати концептуальну модель процесу функціонування цієї системи, а потім провести її формалізацію. На етапі постановки задачі імітаційного моделювання необхідно звернути увагу на існування задачі та необхідність машинного моделювання, а також дослідити задачу за матеріалами літературних джерел. При визначенні вимог до шуканої інформації необхідно сформулювати вимоги до початкової інформації про об’єкт моделювання і організувати отримання інформації, якої недостатньо. Наступний крок — це збирання інформації. Проте в разі неможливості дістати її, потрібно знайти шляхи заміни інформації, якої бракує, чи розробити інші варіанти розв’язання задачі. При цьому не виключено, що постане потреба виконати додаткові економетричні дослідження або застосувати математичну модель (виробничі функції, моделі прогнозування) для знаходження потрібної інформації. У деяких випадках розв’язання задач методом машинної імітації немає змоги здобути всю необхідну інформацію. Для багатьох практично важливих проблем дістати повну інформацію взагалі неможливо. На стадії складання імітаційної моделі іноді відсутні конкретні знання про деякі елементи задачі та умови функціонування системи. Щоб відшукати інформацію, якої бракує, проводять експерименти, висувають гіпотези і приймають (роблять) припущення, що мають бути чітко й точно сформульовані. На етапі визначення параметрів та змінних необхідно: 1) визначити параметри системи; 2) визначити вхідні та вихідні змінні; 3) визначити вплив зовнішнього середовища. Заключним етапом побудови імітаційної моделі є створення її логічної структурної схеми. Далі розробляється машинна схема і відбувається програмування задачі. Логічну схему імітаційної моделі рекомендується створювати за модульним (блоковим) принципом, тобто у вигляді сукупності стандартних блоків-модулів. Побудувавши схему імітаційної моделі, перевіряють її логічну достовірність.

28. Метод Монте-Карло і його застосування для розв'язування детерміно­ваних задач (обчислення визначеного інтегралу).

Метод Монте-Карло являє собою сукупність формальних процедур, засобами яких відтворюються на ЕОМ будь-які випадкові фактори (випадкові події, випадкові величини з довільним розподілом, випадкові вектори тощо). Метод Монте-Карло застосовується в багатьох галузях науки і техніки. За допомогою процедур Монте-Карло розроблено численні методи для обчислення кратних інтегралів, розв’язування інтегральних і диференціальних рівнянь. У задачах оптимізації процедура Монте-Карло використовується для генерування випадкових точок з області визначення цільової функції та установлення випадкових напрямів руху до екстремуму в пошукових методах. Нехай потрібно обчислити інтеграл від деякої функції на заданому відрізку змінювання аргументу. Після нескладних перетворень початкову задачу можна звести до задачі обчислення інтеграла: де 0 £ f (x) £ 1 при 0 £ x £ 1.

Визначимо площу 1-ї фігури, обмеженої кривою y = f (x), віссю x і прямими х = 0, х = 1. Уявімо тепер симетричну дзигу у вигляді десятигранника, кожну з граней якого позначено однією з цифр 0, 1, 2,..., 9. Пустимо дзигу. Після її падіння на верхній грані з однаковою ймовірністю можна очікувати будь-яку з десяти згаданих цифр. Розглянемо два десяткові k-розрядні числа і , значення яких містяться між нулем та одиницею і утворюються так. Пускаючи k раз дзигу, вважатимемо здобуту послідовність цифр десятковими розрядами числа . Повторивши експеримент, дістанемо число . Наприклад, якщо k = 5 і на верхній грані дзиги випали відповідно цифри 0, 3, 7, 0, 5, то шукане число дорівнює 0,03705. Точку з координатами називатимемо випадковою точкою, а спосіб її утворення — киданням. Очевидно, що ймовірність попадання випадкової точки в заштриховану область дорівнює відношенню площі даної фігури, тобто значення інтеграла I, до площі квадрата, яка дорівнює одиниці. Отже, ймовірність попадання випадкової точки в заштриховану область дорівнює значенню шуканого інтеграла. Тому задача обчислення інтеграла зводиться до задачі відшукання ймовірності. Останню оцінимо статистичними методами з допомогою відносної частоти. Кидаємо n випадкових точок на площину квадрата. Нехай виконується умова Тоді точка належить заштрихованій області. Припустимо тепер, що m — число точок, для яких виконується умова. Відносна частота попадання точки в заштриховану область дорівнює . Згідно з теоремою Бернуллі 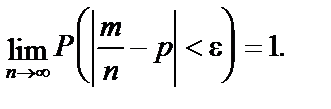. Отже, 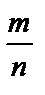є наближеним значенням шуканого інтеграла.