Концептуальна модель обчислювальної системи (ЕОМ з терміналами).

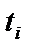1) ЕОМ з допомогою системи розподілених терміналів обслуговує користувачів за правилом черги FIFO «Першим прийшов — першим обслужений». 2) Проміжки часу між послідовними появами заявок — випадкова величина , яка рівномірно розподілена на відрізку [1, 10], набуваючи на ньому всіх цілих значень. 3) Час обслуговування і-ї заявки — випадкова величина, що з однаковою ймовірністю набуває значень 1, 2, 3, 4, 5, 6. 4) Скориставшись імітаційною моделлю, визначити: 1. 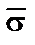— середній час перебування заявок в обчислювальній системі (час очікування і час обслуговування), 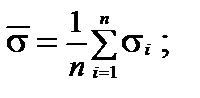тут 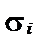— час перебування і-ї заявки в системі; n — кількість заявок. 2. L — відносний час простою ЕОМ, %,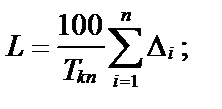

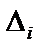тут — час простою ЕОМ безпосередньо перед обслуговуванням і-ї заявки; 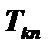— час закінчення обслуговування останньої n-ї заявки. 5) Основні співвідношення: 1. 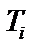— поточний (системний) час — момент надходження і-ї заявки (Т1= 0), 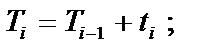2. Toi — час початку обслуговування і-ї заявки, 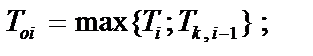3. Tki — час закінчення обслуговування і-ї заявки, 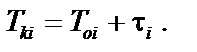Звідси маємо: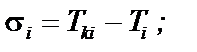

 

 

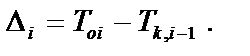
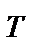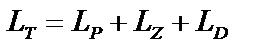20. Статична детермінована модель керування запасами: економіко-ма­те­ма­тична модель.

Оскільки рух запасу циклічний, то для створення економіко-математичної моделі достатньо розглянути один цикл (трикутник на схемі). Схема руху запасу:

Загальні витрати за період : . Витрати на зберігання згідно з шостою передпосилкою наберуть вигляду: 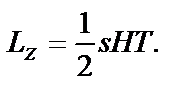Цільова функція — витрати за одиницю часу 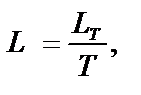або 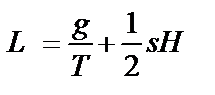. Згідно з другою передпосилкою: 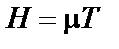. Цільова функція, яку потрібно мінімізувати: .

 

 

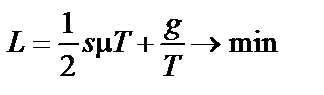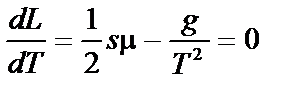Оскільки цільова функція опукла і унімодальна, то її мінімум знаходиться стандартним методом: . Звідси 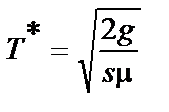. Знайдемо оптимальне значення граничного запасу: 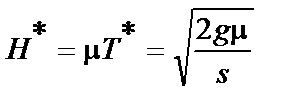. Оскільки в даних умовах граничний запас дорівнює партії поставки, то 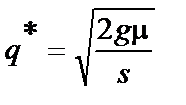. Цю формулу дістав Вільсон (1928 р.), а тому її названо на його честь. Інколи цю формулу називають формулою для визначення найбільш економічної партії поставок. Незважаючи на досить жорсткі та ідеальні умови її створення, формула Вільсона (або її модифікації) часто застосовується на практиці.

 

21. Імітація випадкових подій. Схема випробувань за "жеребкуванням".

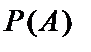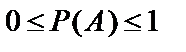Випадкова подія — подія, яка за певних умов може як відбутися, так і не відбутися. Числовою характеристикою міри можливості появи випадкової події A за тих чи інших умов, які можуть повторюватися необмежену кількість разів, є імовірність (). У загальному випадку під час імітаційного моделювання часто виникає потреба імітувати випадкові події, які можуть мати різне призначення. Випадкові події імітуються згідно зі схемою випробувань за «жеребкуванням», сутність якої полягає у такому. Нехай у результаті спроби може настати одна з n несумісних у сукупності подій 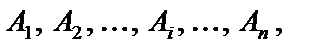що утворюють повну групу, причому 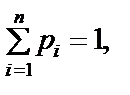де 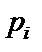— ймовірність появи події 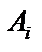. Якщо є генератор випадкових чисел РВП [0, 1], то схему випробувань за «жеребкуванням» можна подати так: 1) Розбиваємо відрізок [0, 1] на n частин завдовжки 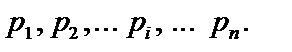Координати точок поділу відрізка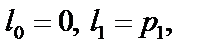 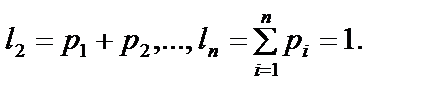2) Обираємо 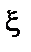— наступне число із РВП [0, 1]. У разі, коли 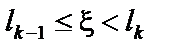, вважаємо, що відбулася подія 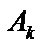. Справді, за такої схеми 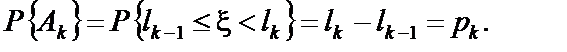Стандартний алгоритм визначення індексу k, з допомогою якого обирається випадкова подія 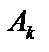, реалізується згідно із схемою, зображеною нижче.