
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 8. Задача о назначениях
Краткое описание сущности задачи – «Лучший работник для выполнения данной работы». В этой задаче необходимо назначить работников на определенные работы; каждый работник может выполнять любую работу, хотя и с различной степенью мастерства. Если на некоторую работу назначается работник именно той квалификации, которая необходима для ее выполнения, тогда стоимость выполнения работы будет ниже, чем при назначении на данную работу работника неподходящей квалификации. Цель задачи – найти оптимальное (минимальной стоимости) распределения работников по всем заявленным работам, то есть найти такую перестановку (р1,р2,..., рn) из чисел 1,2,3,..., n, при которой обеспечен Данные ограничения означают, что один механизм может быть предназначен для выполнения только одной работы. Тогда задача будет состоять в определении таких чисел {хij}, при которых достигается минимум функционала min
Получаем следующую задачу ЛП. Минимизировать при выполнении условий
Задачу о назначениях можно эффективно решить так же, как и транспортную задачу. Вместе с тем тот факт, что все величины спроса и предложения равны 1, привел к разработке упрощенного алгоритма решения, названного венгерским методом. Этот метод также основан на симплекс-методе. Венгерский метод Алгоритм венгерского метода был разработан и опубликован Харолдом Куном в 1955 году. Автор дал ему имя «венгерский метод» в связи с тем, что алгоритм в значительной степени основан на более ранних работах двух венгерских математиков (Кёнига и Эгервари). В 2006 году было обнаружено, что Якоби нашёл решение задачи о назначениях в XIX веке и опубликовал его в 1890 году на латыни.
Оптимальное решение данной задачи ЛП останется неизменным, если ко всем элементам какой-либо строки или столбца матрицы стоимостей ||cij|| прибавить константу или вычесть ее из этих элементов. Таким образом, стоимость cij изменится и будет равна cij’ = cij-pi-qj (8.3) Покажем, что при коэффициентах целевой функции cij’ получим те же оптимальные значения переменных xij, что и при коэффициентах cij.
Поскольку новая целевая функция отличается от исходной только на константу, оптимальные значения переменных xij должны быть одинаковы в обоих случаях. Таким образом показано, что этапы 1 и 2 венгерского метода, где pi вычитаются из элементов строки I, а qj – из элементов столбца j матрицы стоимостей, приводят к эквивалентной задаче о назначениях. Основная идея венгерского метода заключается в переходе от исходной квадратной матрицы стоимости С к эквивалентной ей матрице Сэ с неотрицательными элементами и системой n независимых нулей, из которых никакие два не принадлежат одной и той же строке или одному и тому же столбцу. Для заданного n существует n! допустимых решений. Если в матрице назначения X расположить n единиц так, что в каждой строке и столбце находится только по одной единице, расставленных в соответствии с расположенными n независимыми нулями эквивалентной матрицы стоимости Сэ, то получим допустимые решения задачи о назначениях. Следует иметь в виду, что для любого недопустимого назначения соответствующая ему стоимость условно полагается равной достаточно большому числу М в задачах на минимум. Если исходная матрица не является квадратной, то следует ввести дополнительно необходимое количество строк или столбцов, а их элементам присвоить значения, определяемые условиями задачи, возможно после редукции, а доминирующие альтернативы дорогие или дешевые исключить.
Пример 1 Таблица 1
Этап 1. В исходной матрице стоимостей определим в каждой строке минимальную стоимость и отнимаем ее от других элементов строки. Этап 2. В матрице, полученной на первом этапе, найдем в каждом столбце стоимостей минимальную стоимость qj и отнимаем ее от других элементов. Таблица 2.
Этап 3. оптимальным назначениям будут соответствовать нулевые элементы, полученные на предыдущем этапе. Таблица 3.
В последней матрице подчеркнутые нулевые элементы определяют оптимальное решение. В некоторых случаях нулевые элементы, полученные на первом и втором этапе венгерского метода, не позволяют непосредственно получать допустимое решение. Тогда необходимы дополнительные действия. Пример 2. Таблица 4.
Таблица 5.
В этой матрице расположение нулевых элементов не позволяет назначить каждому исполнителю одну работу.
Этап 2.1. i. В последней матрице провести минимальное число горизонтальных и вертикальных прямых по стокам и столбцам, чтобы вычеркнуть в матрице все нулевые элементы. ii. Найти наименьший не вычеркнутый элемент и вычесть его из остальных не вычеркнутых элементов и прибавить к элементам, стоящим на пересечении проведенных на предыдущем этапе прямых. iii. Если новое распределение нулевых элементов не позволяет построить допустимое решение, повторить этап 2.1. В противном случае перейти к третьему этапу алгоритма.
Значение целевой функции равно 1+10+5+5=21;.такое же значение можно получить суммированием значений pi и qj и значения элемента, наименьшего среди всех не вычеркнутых: (1+7+4+5) + (0+0+3+0) + (1)=21.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 463; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.186.218 (0.006 с.) |
 по всем перестановкам (р1,р2,..., рn). Каждая такая перестановка может быть представлена точкой в п2- мерном евклидовом пространстве или в виде матрицы Хп..
по всем перестановкам (р1,р2,..., рn). Каждая такая перестановка может быть представлена точкой в п2- мерном евклидовом пространстве или в виде матрицы Хп..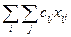 при ограничениях (8.1). Задача о назначениях является как примером экстремальной комбинаторной задачи целочисленного линейного программироваия (в данных задачах необходимо найти экстремум некоторой целевой функции, заданной на конечном множестве, элементами которого служат перестановки из n символов (объектов)), так и частным случаем транспортной задачи, в которой работники соответствуют пунктам отправления, а работы – пунктам назначения. В данном случае все величины спроса и предложения равны 1. Задачу о назначении n работников на n видов работ можно представить в виде задачи линейного программирования следующим образом. Обозначим через cij стоимость назначения работника i на работу j и определим
при ограничениях (8.1). Задача о назначениях является как примером экстремальной комбинаторной задачи целочисленного линейного программироваия (в данных задачах необходимо найти экстремум некоторой целевой функции, заданной на конечном множестве, элементами которого служат перестановки из n символов (объектов)), так и частным случаем транспортной задачи, в которой работники соответствуют пунктам отправления, а работы – пунктам назначения. В данном случае все величины спроса и предложения равны 1. Задачу о назначении n работников на n видов работ можно представить в виде задачи линейного программирования следующим образом. Обозначим через cij стоимость назначения работника i на работу j и определим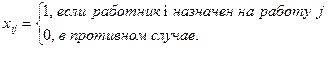 (8.1)
(8.1)
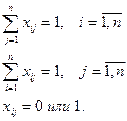 (8.2)
(8.2)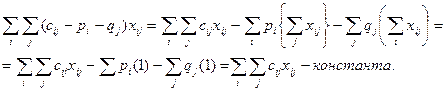 (8.4)
(8.4)


