
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 3. Математическое программированиеСодержание книги
Поиск на нашем сайте
Лекция 3. Математическое программирование Содержательные постановки задач, приводящие к моделям линейного программирования.
Во второй половине XX в. при решении практических задач стали находить широкое применение математические методы. Они стали использоваться при перспективном и текущем планировании научно-исследовательских работ, проектировании различных объектов, управлении технологическими и производственными процессами, прогнозировании развития социальных и производственных систем, оптимизации маршрутов перевозки грузов. Особенно часто к математическим методам прибегают при решении задач оптимизации функционирования производственных систем, при распределении материальных и трудовых ресурсов и страховых запасов, при выборе местоположения предприятий, исследовании и оценке безопасности функционирования объектов повышенного риска. Постановки перечисленных задач носят оптимизационный характер, где в качестве критериев эффективности применяются различные целевые функции. Как уже было отмечено, особенностью постановок задач системного анализа является то обстоятельство, что наряду со строгим математическим аппаратом применяются эвристические методы, основанные на интуиции исследователя, его опыте в решении задач подобного типа. Рассмотрим некоторые постановки задач, являющиеся типовыми задачами системных исследований. Математическая формулировка задачи об оптимальном использовании ресурсов Для изготовления n видов продукции используется m видов ресурсов. Обозначим через xj…-число единиц j-го вида продукции (j=1,…,n), запланированной к производству; bi- запас i-го ресурса (i=1,…,m) aij…-число единиц ресурса i, затрачиваемого на изготовление единицы продукции j-го вида (aij- технологические коэффициенты); cj- выручка от реализации единицы продукции j-го вида (или цена продукции j-го вида). Тогда экономико-математическая модель задачи об использовании ресурсов в общей постановке примет вид: Найти такой план X=(x1, …, xn) выпуска продукции, который удовлетворял бы системе ограничений:
и при котором целевая функция достигала бы своего максимального значения
Задача о смесях. В такого рода задачах обычно требуется минимизировать затраты на приготовление некоторой смеси, соблюдая при этом ограничения на наличие в данной смеси полезных веществ.
Лекция 7. Содержательные постановки задач линейного программирования. Методы решения задач линейного программирования
Лекция 4. Пример решения задачи линейного программирования. Рассмотрим следующую задачу. Компания производит краску для внутренних и наружных работ из сырья двух типов: М1 и М2. Существуют ограничения на расход сырья (таблица 2) и ограничения по спросу на готовую продукцию. Первое ограничение указывает, что ежедневный объем производства краски для внутренних работ не должен превышать ежедневный объем производства краски для наружных работ более, чем на одну тонну. Второе ограничение таково: максимальный ежедневный объем производства краски для внутренних работ не должен превышать 2 т.
Таблица 2. Исходные данные по расходу сырья.
Сформулируем задачу линейного программирования в следующем виде: найти максимум линейной формы 5х1 + 4 х2 при ограничениях 6x1 + 4 х2 ≤ 24; x1 + 2 х2 ≤ 6; -x1 + х2 ≤ 1; х2 ≤ 2; х 1, х 2 > 0.
Каноническая форма задачи линейного программирования будет иметь вид 5 x 1 + 4 x 2 + 0 x 3 + 0 x 4 + 0 x 5 + 0 x 6→ max; 6 х 1 + 4 х 2 + 1 х 3 + 0 x 4 + 0 x 5 + 0 x 6= 24; х 1 + 2 х 2 + 0 х 3 + 1 x 4 + 0 x 5 + 0 x 6= 6; - х 1 + х 2 + 0 х 3 + 0 x 4 + 1 x 5 + 0 x 6= 1; х 2+ 0 х 3 + 0 x 4 + 0 x 5 + 1 x 6=2; xi ≥0, i =1,…,6
Составим исходную симплекс-таблицу (табл. 3).
Таблица 3
Небазисные (нулевые) переменные х 1 и х 2; базисные переменные х 3, x 4, x 5, x 6 Поскольку -5 < -4 < 0, то в качестве направляющего выбираем столбец A 1. Составив отношение вида min Таблица 4
На данном этапе в качестве направляющего столбца выбираем второй, направляющая строка - третья, т.к. из
Табл. 5.
Поскольку в индексной строке все элементы положительны, это означает, что найдено оптимальное решение х1*= 3, х2 = Пример 11.1. Составить двойственную задачу по отношению к задаче, состоящей в максимизации функции
при условиях
Решение. Для данной задачи
Число переменных в двойственной задаче равно числу уравнений в системе (6.5), т. е. равно трем. Коэффициентами в целевой функции двойственной задачи являются свободные члены системы уравнений (6.5), т.е. числа 12, 24, 18. Целевая функция исходной задачи (6.4) – (6.6) исследуется на максимум, а система условий (6.5) содержит неравенства. Поэтому в двойственной задаче целевая функция исследуется на минимум. Так как все три переменные исходной задачи (6.4) – (6.5) принимают только лишь неотрицательные значения, то в системе условий двойственной задачи должны быть три неравенства. Следовательно, для задачи (6.4) – (6.5) двойственная задача такова: найти минимум функции
Значение целевой функции в задачах равно 34.8
11.2. Решение задач линейного программирования с использованием программного обеспечения MATLAB
В состав MATLAB входит Optimization Toolbox, предназначенный для решения линейных и нелинейных оптимизационных задач. Задача линейного программирования состоит в нахождении вектора x, который минимизирует целевую линейную функцию fTx при условии A X≤ B; X≥0, где с =(с1, c2,…,cn) представляет собой n-мерный вектор, составленный из коэффициентов целевой функции, причем cT – транспонированная вектор- строка; x=(x1. xn) – n –мерный вектор переменных решений, B=[b1 b2 m-мерный вектор свободных членов bm] Beq=[beq1 … beqr] ограничения в виде равенств; двусторонние покомпонентные ограничения в векторной форме lb≤x≤ub A= Пример: задача составления рациона питания Имеются 3 продукта П1, П2 и П3 разной цены, каждый из которых содержит определенное количество питательных ингридиентов И1, И2, И3, И4. Известно, что в день требуется: И1не менее 250, И2 не менее 60, И3 не менее 100 и И4 не менее 220. Требуется минимизировать затраты на приобретение продуктов. Очевидно, что количество приобретаемых процессов не может быть отрицательным.. Записываем целевую функцию, матрицу A, векторы b и lb в соответствии с требованиями Toolbox, обозначив искомые количества продуктов через x1, x2 и x3 соответственно. Поскольку линейные ограничения содержат «меньшк или равно», а количество ингредиентов в рационе не может быть менее заданных величин, то следует изменить знаки обеих частей системы.При вызове программы linprog вместо неиспользуемых ограничение (нет ограничений в виде равенств) задайте пустые массивы, обозначаемые в MATLAB пустыми скобками. Программа ration % задание матрицы и вектора правой части системы неравенств A=[4 6 15 2 2 0 5 3 4 7 3 12] A=-A; b=[250 60 100 220]; b=-b; % Определение коэффициентов целевой функции f=[44; 35; 100]; % Задание ограничений снизу на переменные lb=[0; 0; 0]; % решение и вывод результата в командное окно x=linprog(f,A,b,[],[],lb) Постановка задачи Под термином "транспортные задачи" понимается широкий круг задач не только транспортного характера. Общим для них является, как правило, распределение ресурсов, находящихся у m производителей (поставщиков), по n потребителям этих ресурсов. В качестве критериев в транспортных задачах используют: критерий стоимости (план перевозок оптимален, если достигнут минимум затрат на его реализацию), критерий времени (план оптимален, если на его реализацию затрачивается минимум времени) и другие. Наиболее часто встречаются следующие задачи, относящиеся к транспортным: · прикрепление потребителей ресурса к производителям; · привязка пунктов отправления к пунктам назначения; · взаимная привязка грузопотоков прямого и обратного направлений; · отдельные задачи оптимальной загрузки промышленного оборудования; · оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями и др. Рассмотрим экономико-математическую модель прикрепления пунктов отправления к пунктам назначения. Имеются m пунктов отправления груза и объемы отправления по каждому пункту a 1, a 2,..., am. Известна потребность в грузах b 1, b 2,..., bn по каждому из n пунктов назначения. Задана матрица стоимостей доставки по каждому варианту cij, В общем виде исходные данные представлены в табл. 7.1. Строки транспортной таблицы соответствуют пунктам отправления (в последней клетке каждой строки указан объем запаса продукта ai ), а столбцы - пунктам назначения (последняя клетка каждого столбца содержит значение потребности bj). Все клетки таблицы (кроме тех, которые расположены в нижней строке и правом столбце) содержат информацию о перевозке из i -го пункта в j -й: в правом верхнем углу находится цена перевозки единицы продукта, а в левом нижнем - значение объема перевозимого груза для данных пунктов. Таблица 7.1. Исходные данные
Транспортная задача называется закрытой, если суммарный объем отправляемых грузов
Если такого равенства нет (потребности выше запасов или наоборот), запасу называют открытой, т.е.:
Для написания модели необходимо все условия (ограничения) и целевую функцию представить в виде математических уравнении. Все грузы из i-х пунктов должны быть отправлены, т.е.:
Все j-е пункты (потребители) должны быть обеспечены грузами в плановом объеме:
Суммарные объемы отправления должны равняться суммарным объемам назначения (3.1). Должно выполняться условие неотрицательности переменных:
Перевозки необходимо осуществить с минимальными транспортными издержками (функция цели):
Вместо матрицы стоимостей перевозок (cij) могут задаваться матрицы расстояний. В таком случае в качестве целевой функции рассматривается минимум суммарной транспортной работы. Как видно из выражения (7.1), уравнение баланса является обязательным условием решения транспортной задачи. Поэтому, когда в исходных условиях дана открытая задача, то ее необходимо привести к закрытой форме. В случае, если - потребности по пунктам назначения превышают запасы пунктов отправления, то вводится фиктивный поставщик с недостающим объемом отправления с объемом запасов. равным;
- запасы поставщиков превышают потребности потребителей, то вводится фиктивный потребитель с необходимым объемом потребления, равным:
Варианты, связывающие фиктивные пункты с реальными, имеют нулевые оценки. После введения фиктивных пунктов задача решается как закрытая. Транспортным задачам присущи следующие особенности: - распределению подлежат однородные ресурсы; - условия задачи описываются только уравнениями; - все переменные выражаются в одинаковых единицах измерения; - во всех уравнениях коэффициенты при неизвестных равны единице; - каждая неизвестная встречается только в двух уравнениях системы ограничений. Транспортные задачи могут решаться симплекс-методом. Однако перечисленные особенности позволяют для транспортных задач применять более простые методы решения. Опорный план является допустимым решением транспортной задачи и используется в качестве начального базисного решения при нахождении оптимального решения методом потенциалов. Существует три метода нахождения опорных планов: метод северо-западного угла, метод минимального элемента и метод Фогеля. "Качество" опорных планов, полученных этими методами, различается: в общем случае метод Фогеля дает наилучшее решение (зачастую оптимальное), а метод северо-западного угла – наихудшее. Все существующие методы нахождения опорных планов отличаются только способом выбора клетки для заполнения. Само заполнение происходит одинаково независимо от используемого метода. 7.2. Методы составления начального опорного плана Базисный план составляется последовательно, в несколько шагов (точнее, m + n - 1 шагов). На каждом из этих шагов заполняется одна клетка, притом так, что, либо полностью удовлетворяется один из заказчиков (тот, в столбце которого находится заполняемая клетка), либо полностью вывозится весь запас груза с одной из баз (с той, в строке которой находится заполняемая клетка).
- В первом случае мы можем исключить столбец, содержащий заполненную на этом шаге клетку, и считать, что задача свелась к заполнению таблицы с числом столбцов, на единицу меньшим, чем было перед этим шагом, но с тем же количеством строк и с соответственно измененным запасом груза на одной из баз (на той базе, которой был удовлетворен заказчик на данном шаге). - Во втором случае исключается строка, содержащая заполняемую клетку, и считается, что таблица сузилась на одну строку при неизменном количестве столбцов и при соответствующем изменении потребности заказчика, в столбце которого находится заполняемая клетка. Начиная с первоначально данной таблицы и повторив (m + n - 2) раз описанный шаг, мы придем к “таблице”, состоящей из одной строки и одного столбца (иначе говоря, из одной пустой клетки). Другими словами, мы пришли к задаче с одной базой и с одним потребителем, причем потребности этого единственного заказчика равны запасу груза на этой единственной базе. Заполнив последнюю клетку, мы освобождаем последнюю базу и удовлетворяем потребность последнего заказчика. В результате, совершив (m + n - 1) шагов, мы и получим искомый опорный план. Замечание. Может случиться, что уже на некотором (но не на последнем!) шаге потребность очередного заказчика окажется равной запасу груза на очередной базе. Тогда после заполнения очередной клетки объем таблицы как бы одновременно уменьшается на одни столбец и на одну строку. Но и при этом мы должны считать, что уменьшение объема таблицы происходит либо на один столбец, а на базе сохраняется "остаток" равный нулю, либо на одну строку, а у заказчика еще осталась неудовлетворенная "потребность" в количестве нуля единиц груза, которая и удовлетворяется на одном из следующих шагов. Этот нуль ("запас" или "потребностью" – безразлично) надо записать в очередную заполняемую клетку на одном из последующих шагов. Так как при этом оказывается равной нулю одна из базисных неизвестных, то мы имеем дело с вырожденным случаем. 1. Диагональный метод, или метод северо-западного угла. При этом методе на каждом шаге построения первого опорного плана заполняется левая верхняя клетка (северо-западный угол) оставшейся части таблицы. При таком методе заполнение таблицы начинается с клетки неизвестного x 11 и заканчивается в клетке неизвестного xmn, т. е. идет как бы по диагонали таблицы перевозок.
Пример
Заполнение таблицы начинается с ее северо-западного угла, т.е. клетки с неизвестным x 11. Первая база A 1 может полностью удовлетворить потребность первого заказчика B 1 (a 1=300, b 1=170, a 1 > b 1). Полагая x 11= 170, вписываем это значение в клетку x 11 и исключаем из рассмотрения первый столбец. На базе A 1 остается измененный запас Теперь переходим к заполнению клетки для неизвестного x 23 и т.д. Через шесть шагов у нас останется одна база A 3 с запасом груза (остатком от предыдущего шага) Общий объем перевозок в тонно-километрах для этого плана составит
2. Метод наименьшей стоимости. При этом методе на каждом шаге построения опорного плана первою заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф. Если такая клетка не единственная, то заполняется любая из них. Пример
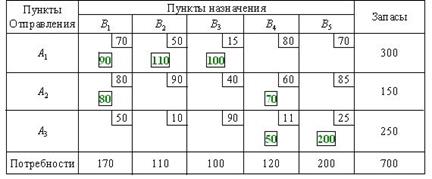
В данном случае заполнение таблицы начинается с клетки для неизвестного x 32, для которого мы имеем значение c 32 = 10, наименьше из всех значений cij. Эта клетка находится на пересечении третьей строки и второго столбца, соответствующим третьей базе A 3 и второму заказчику B 2. Третья база A 3 может полностью удовлетворить потребность второго заказчика B 2 (a 3=250, b 2=110, a 3 > b 2). Полагая x 32 = 110, вписываем это значение в клетку x 32 и исключаем из рассмотрения второй столбец. На базе A 3 остается изменённый запас
На пятом шаге клеток с наименьшими значениями cij оказалось две (c 11= c 15=70). Мы заполнили клетку для x 15 , положив x 15 = 180. Можно было выбрать для заполнения другую клетку, положив x 11 = 170, что приведет в результате к другому опорному плану. Общий объем перевозок в тонно-километрах для этого плана составит
Замечание. В диагональном методе не учитываются величины тарифов, в методе же наименьшей стоимости эти величины учитываются, и часто последний метод приводит к плану с меньшими общими затратами (что и имеет место в нашем примере), хотя это и не обязательно. Кроме рассмотренных выше способов иногда используется, так называемый, метод Фогеля. Суть его состоит в следующем: В распределительной таблице по строкам и столбцам определяется разность между двумя наименьшими тарифами. Отмечается наибольшая разность. Далее в строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза в дальнейшем в расчет не принимаются. На каждом этапе загружается только одна клетка. Распределение груза производится, как и ранее.
Понятие потенциала и цикла Для перехода от одного базиса к другому при решении транспортной задачи используются так называемые циклы. Циклом пересчета или короче, циклом в таблице перевозок называется последовательность неизвестных, удовлетворяющая следующим условиям: 1. Одно из неизвестных последовательности свободное, а все остальные – базисные. 2. Каждые два соседних в последовательности неизвестных лежат либо в одном столбце, либо в одной строке. 3. Три последовательных неизвестных не могут находиться в одном столбце или в одной строке. 4. Если, начиная с какого-либо неизвестного, мы будем последовательно переходить от одного к следующему за ним неизвестному то, через несколько шагов мы вернемся к исходному неизвестному. Второе условие означает, что у двух соседних неизвестных в цикле либо первые, либо вторые индексы одинаковы. Если каждые два соседних неизвестных цикла соединить отрезком прямой, то будет получено геометрическое изображение цикла – замкнутая ломаная из чередующихся горизонтальных и вертикальных звеньев, одна из вершин которой находится в свободной клетке, а остальные - в базисных клетках. Можно доказать, что для любой свободной клетки таблицы перевозок существует один и только один цикл, содержащий свободное неизвестное из этой клетки, и что число вершин в цикле всегда четно. Так, например, в таблице перевозок, составленной по диагональному методу при решения задачи из предыдущего пункта, неизвестному x 21 соответствует цикл x 21, x 23, x 13, x 11, x 21 и т.д. Пусть теперь мы имеем некоторую свободную клетку с соответствующим ей циклом. Если мы изменим значение свободного неизвестного, увеличив его на некоторое число x, то, переходя последовательно от одной вершины цикла к другой, мы должны будем в силу неизменности сумм по строкам и по столбцам поочередно уменьшать и увеличивать значения неизвестных в цикле на то же число x. Например, в указанном выше цикле для свободного неизвестного x 21 получим: старые значения: x 21= 0, x 23= 80, x 13= 20, x 11= 170, x 21= 0; новые значения: Очевидно, если снабдить вершины цикла поочередно знаками "+" и "–", приписав вершине в свободной клетке знак "+", то можно сказать, что в вершинах со знаком "+" число x прибавляется к прежнему значению неизвестного, находящегося в этой вершине, а в вершинах со знаком "–" это число x вычитается из прежнего значения неизвестного, находящегося в этой вершине. Замечание. Так как число вершин в цикле всегда четно, то, возвращаясь в свободную клетку, мы должны будем приписать ей знак "+", т. е. тот знак, который ей уже приписан при выходе из нее. Это очень существенное обстоятельство, так как иначе мы пришли бы к противоречию. Безразлично также, в каком направлении обходится цикл при “означивании” вершин. Если в качестве x выбрать наименьшее из чисел, стоящих в вершинах, снабженных знаком "–", то, по крайней мере, одно из прежних базисных неизвестных примет значение нуль, и мы можем перевести его в число свободных неизвестных, сделав вместо него базисным то неизвестное, которое было свободным. Так, например, в рассмотренном выше цикле имеем отрицательные вершины x 21 и x 11 ; следовательно, выбрав х = min {80; 170} = 80, мы получаем: старые значения: x 21= 0, x 23= 80, x 13= 20, x 11= 170, x 21= 0; новые значения: т. е. вместо прежнего базисного решения получаем новое базисное решение:
Выбор в качестве x минимального среди чисел, стоящих в отрицательных вершинах цикла, обеспечивает допустимость нового базиса. Если минимальное значение среди базисных неизвестных, стоящих в отрицательных вершинах цикла, принимается не в одной отрицательной вершине, то свободной оставляют только одну из них, а в других клетках с тем же минимальным значением пишут нули. В этом случае новое базисное решение будет вырожденным. Может случиться, что и само минимальное значение среди чисел в отрицательных клетках равно нулю. Тогда преобразование таблицы перевозок сведется к перестановке этого нуля в свободную клетку. Значения всех неизвестных при этом остаются неизменными, но решения считаются различными, так как различны базисы. Оба решения вырождены. Описанное выше преобразование таблицы перевозок, в результате которого преобразуется базис, называется пересчетом по циклу. Заметим, что неизвестные, не входящие в цикл, этим преобразованием не затрагиваются, их значения остаются неизменными и каждое из них остается либо в группе базисных, либо в группе свободных неизвестных, как и до пересчета. Выясним теперь, как пересчет по циклу влияет на общий объем затрат на перевозки и при каком условии эти затраты становятся меньше. Пусть xpq – некоторое свободное неизвестное, для которого мы построили цикл и осуществили пересчет по циклу с некоторым числом x. Если вершине цикла, находящейся в i -й строке и j -м столбце таблицы перевозок, приписан знак "+", то значение неизвестного xij, находящегося в этой вершине, увеличивается на x, что в свою очередь вызывает увеличение затрат на cij x, где cij – тариф, соответствующий этой клетке; если же указанной вершине приписан знак “–”, то значение неизвестного xij уменьшается на x, что вызывает уменьшение затрат на cij x. Сложим тарифы, соответствующие положительным вершинам цикла, и вычтем из этой суммы сумму тарифов, соответствующих отрицательным вершинам цикла; полученную разность Spq назовем алгебраической суммой тарифов для данного свободного неизвестного xpq. Подсчет алгебраической суммы тарифов можно истолковать и так: припишем тарифам те же знаки, которые приписаны соответствующим вершинам цикла, тогда алгебраическая сумма тарифов равна сумме таких тарифов со знаком (“относительных тарифов”). Теперь, очевидно, мы можем, заключить, что в целом при пересчете но циклу, соответствующему свободному неизвестному xpq общий объем затрат на перевозки изменится на произведение алгебраической суммы тарифов на x, т. е. на величину Spqx. Следовательно, если алгебраическая сумма тарифов для некоторого свободного неизвестного xpq отрицательна (Spq < 0), то пересчет по циклу, соответствующему этому неизвестному, приводит к уменьшению общей суммы затрат на реализацию плана перевозок. Если же алгебраическая сумма тарифов положительна (Spq > 0), то пересчет по соответствующему циклу приведет к увеличению общей суммы затрат. И, наконец, если алгебраическая сумма тарифов равна нулю (Spq = 0), то пересчет по соответствующему циклу не изменит общую сумму затрат (два различных базисных плана требуют одинаковых затрат на их реализацию). Так, например, для цикла x 21, x 23, x 13, x 11, x 21 в рассмотренной задаче алгебраическая сумма тарифов
Значит, пересчет по этому циклу снижает расходы. И действительно, осуществив такой пересчет, мы получаем план, по которому объем перевозок в тонно-километрах составляет
тогда как по исходному плану он составил S 1= 30650. Имеем снижение объема перевозок на 1200 тонно-километров, что и следовало ожидать, так как алгебраическая сумма тарифов в данном случае равна –15, а пересчет по циклу осуществляется с помощью числа х = 80 (изменение затрат равно -15*80 = - 1200). Шаг 2. Ячейки, образующие цикл для свободной ячейки A3B2: A3B2, A3B4, A2B4, A2B1, A1B1, A1B2
F=29400 ден. ед.
Вычисление алгебраической суммы тарифов для каждого из свободных неизвестных можно производить без построения соответствующего цикла, пользуясь так называемыми потенциалами. Припишем каждой базе Ai,, некоторое число ui, и каждому потребителю Bj некоторое число vj:
так что ui, + vj = cij, (7.6) где cij – тарифы, соответствующие клеткам, заполненным базисными неизвестными. Эти числа ui, и vj называются потенциалами соответствующих баз и потребителе
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 201; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.49.90 (0.011 с.) |

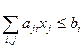
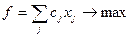
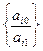 , определяем направляющую строку. Для этого находим минимальное отношение
, определяем направляющую строку. Для этого находим минимальное отношение Следовательно, направляющая строка - первая, направляющий элемент — а11=1- Применив первый шаг симплексного преобразования, получим новую таблицу (табл. 4).
Следовательно, направляющая строка - первая, направляющий элемент — а11=1- Применив первый шаг симплексного преобразования, получим новую таблицу (табл. 4).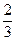
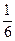
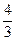
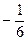

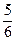
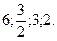 наименьший элемент равен 3/2. Применим следующий шаг симплексного преобразования. В результате получим табл. 5.
наименьший элемент равен 3/2. Применим следующий шаг симплексного преобразования. В результате получим табл. 5.
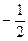
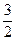
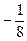

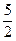
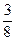


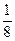
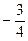
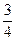
 , искомое значение целевой функции равно 5 х1 + 4х2= 21.
, искомое значение целевой функции равно 5 х1 + 4х2= 21.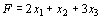 (11.4)
(11.4)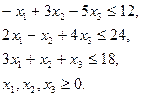 (6.5)
(6.5) и
и 
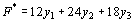 при условиях
при условиях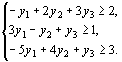

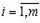
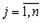 . Необходимо рассчитать оптимальный план перевозок, т.е. определить, сколько груза должно быть отправлено из каждого i -го пункта отправления (от поставщика) в каждый j -ый пункт назначения (до потребителя) xij с минимальными транспортными издержками.
. Необходимо рассчитать оптимальный план перевозок, т.е. определить, сколько груза должно быть отправлено из каждого i -го пункта отправления (от поставщика) в каждый j -ый пункт назначения (до потребителя) xij с минимальными транспортными издержками.
 .равен суммарному объему потребности в этих грузах по пунктам назначения
.равен суммарному объему потребности в этих грузах по пунктам назначения 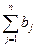 :
: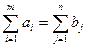 (2.1)
(2.1)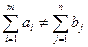
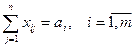 (2.3)
(2.3)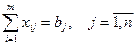 (2.4)
(2.4) (2.5)
(2.5) (2.6)
(2.6)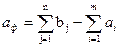 (2.7)
(2.7)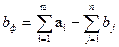 (2.8)
(2.8)
 . В оставшейся новой таблице с тремя строками A 1, A 2, A 3 и четырьмя столбцами B 1, B 2, B 3, B 4; северо-западным углом будет клетка для неизвестного x 12. Первая база с запасом
. В оставшейся новой таблице с тремя строками A 1, A 2, A 3 и четырьмя столбцами B 1, B 2, B 3, B 4; северо-западным углом будет клетка для неизвестного x 12. Первая база с запасом 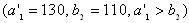 . Полагаем x 12 = 110, вписываем это значение в клетку x 12 и исключаем из рассмотрения второй столбец. На базе A 1 остается новый остаток (запас)
. Полагаем x 12 = 110, вписываем это значение в клетку x 12 и исключаем из рассмотрения второй столбец. На базе A 1 остается новый остаток (запас) 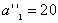 . В оставшейся новой таблице с тремя строками A 1, A 2, A 3 и тремя столбцами B 3, B 4, B 5 северо-западным углом будет клетка для неизвестного x 13. Теперь третий заказчик B 3 может принять весь запас с базы A 1
. В оставшейся новой таблице с тремя строками A 1, A 2, A 3 и тремя столбцами B 3, B 4, B 5 северо-западным углом будет клетка для неизвестного x 13. Теперь третий заказчик B 3 может принять весь запас с базы A 1 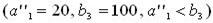 . Полагаем x 13 = 20, вписываем это значение в клетку x 13 и исключаем из рассмотрения первую строку. У заказчика из B 3 осталась еще не удовлетворенной потребность
. Полагаем x 13 = 20, вписываем это значение в клетку x 13 и исключаем из рассмотрения первую строку. У заказчика из B 3 осталась еще не удовлетворенной потребность 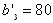 .
. и один пункт B 5 с потребностью b 5=200. Соответственно этому имеется одна свободная клетка, которую и заполняем, положив x 35=200. План составлен. Базис образован неизвестными x 11, x 12, x 13, x 23, x 24, x 34, x 35. Правильность составленного плана легко проверить, подсчитав суммы чисел, стоящих в заполненных клетках по строкам и столбцам.
и один пункт B 5 с потребностью b 5=200. Соответственно этому имеется одна свободная клетка, которую и заполняем, положив x 35=200. План составлен. Базис образован неизвестными x 11, x 12, x 13, x 23, x 24, x 34, x 35. Правильность составленного плана легко проверить, подсчитав суммы чисел, стоящих в заполненных клетках по строкам и столбцам.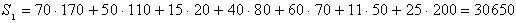
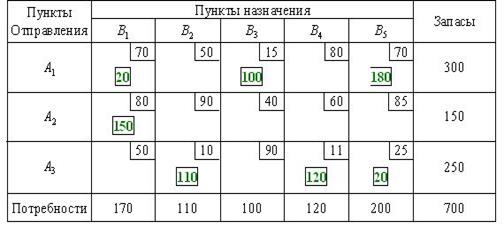
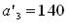 . В оставшейся новой таблице с тремя строками A 1, A 2, A 3 и четырьмя столбцами B 1, B 3, B 4, B 5 клеткой с наименьшим значением cij клетка, где c 34=11. Заполняем описанным выше способом эту клетку и аналогично заполняем следующие клетки. В результате оказываются заполненными (в приведенной последовательности) следующие клетки:
. В оставшейся новой таблице с тремя строками A 1, A 2, A 3 и четырьмя столбцами B 1, B 3, B 4, B 5 клеткой с наименьшим значением cij клетка, где c 34=11. Заполняем описанным выше способом эту клетку и аналогично заполняем следующие клетки. В результате оказываются заполненными (в приведенной последовательности) следующие клетки:

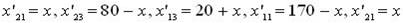
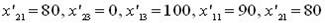
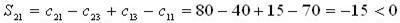 .
.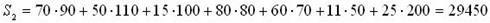
 ,
,


