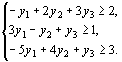Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 5. Двойственная задача линейного программированияСодержание книги
Поиск на нашем сайте
Двойственная задача в линейном программировании строится по формальным правилам на базе другой задачи линейного программирования, называемой основной. Например, если основная задача имеет вид Ах ≤b, х≥0, f (с,х) → max, (6.1) то двойственная к ней задача также является задачей линейного программирования: АТу≥ с, у≥0, f(b, у) → min. (6.2) Здесь х = (x1,х2,...,хn); b = (b1, b2,…,bт); с = (с1, с2,..., сn); у = (y1,y2,... ,уm);
(b,y)= Основная и двойственная к ней задачи образуют пару взаимно двойственных задач: двойственная задача к двойственной оказывается основной задачей. Отношение между прямой и двойственной задачами находи выражение в виде следующих правил: 1) если прямая задача является задачей максимизации, то двойственная задача будет задачей минимизации и наоборот; 2) коэффициенты целевой функции прямой задачи с = (с1, с2,..., сn) становятся свободными членами ограничений двойственной задачи; 3) свободные члены ограничений прямой задачи b = (b1, b2,…,bт) становятся коэффициентами целевой функции двойственной задачи; 4) матрицу ограничений двойственной задачи получают транспонированием матрицы ограничений прямой задачи; 5) знаки неравенств в ограничениях изменяются на обратные; 6) число ограничений прямой задачи равно числу переменных двойственной задачи, а число ограничений двойственной задачи равно числу переменных прямой задачи.
Основная теорема двойственности: Либо обе задачи двойственной пары разрешимы, и тогда (с, х*) = (b, у*), либо обе задачи не имеют решения. Здесь х*,у* - оптимальные планы пары двойственных задач. Эта и ряд других теорем, относящихся к двойственным задачам, играют важную роль при качественном анализе задач линейного программирования. Содержательный анализ двойственной задачи, в том числе и неизвестных у1 у2,..., уm, полностью определяется содержательным смыслом прямой задачи. Так, например, если основная задача (6.1) является задачей производственного планирования, где А - технологическая матрица, b i - количество i-го ресурса, x j - объем выпуска j- го продукта, i = 1, 2,... m, j = 1, 2,... n, то целью решения двойственной задачи (6.2) оказывается нахождение так называемых двойственных оценок ресурсов yi, которые также называют маргинальными (предельными) данными ресурсов. Маргинальные цены, очевидно, связаны только с производством и потому отличаются от обычных рыночных цен на ресурсы. Если маргинальные цены не превосходят рыночных (уi *≤ q i, i =1,2,..., m), то производство, для которого они были рассчитаны, не сможет получить прибыль р от своей производственной деятельности: для любого плана выпуска x р(х) = (с, х) - (b, q) ≤, (с, х*) - (b, q) ≤ (с, х*) - (b, у *) = 0. И, наоборот, если уi * > q i, i = 1, 2,..., т, то реализация оптимального производственного плана х* принесет положительную прибыль. р(х*) = (с, х*) - (b, q) = (А, у*) - (b, q) = (b, y*-q)> 0, размер которой ограничивается: а) средствами, выделяемым на закупку ресурсов; b) объемом рынка ресурсов; с) технологическими условиями производства. Из теоремы двойственности вытекает ряд положений, которые позволяют устанавливать некоторые соотношения между целевой функцией и ресурсами, необходимыми для достижения цели. В частности, следующее важное утверждение: Если задача линейного программирования не вырождена и С(х*) представляет собой максимум ее линейной формы Таким образом, с математической точки зрения оптимальные оценки определяют влияние свободных членов b, условий-ограничений на оптимальную величину целевой функции. Иными словами, вычисление наряду с оптимальным планом х* = (х1*, х2*,..., хn*) связанных с ним оптимальных оценок у* = {у1*, у2*,..., yт*) позволяет ввести относительную важность отдельных ресурсов (b1*, b2*.....bm*) для достижения поставленной цели (максимизации На основе установления такой взаимосвязи между х* и у* можно исследовать влияние небольших отклонений ресурсов на изменение оптимального значения целевой функции, получать маргинальные оценки (идея которых рассмотрена выше), получать другие рекомендации, полезные при разработке и корректировке планов в тех случаях, когда не может быть найдено строгое решение задачи оптимизации. Идеи теории двойственности находят важное применение в разработке численных методов линейного программирования, позволяющих решать задачи с неопределенностью, не имеющие строгого оптимума, что имеет особое значения для задач системного анализа. Пример 11.1. Составить двойственную задачу по отношению к задаче, состоящей в максимизации функции
при условиях
Решение. Для данной задачи
Число переменных в двойственной задаче равно числу уравнений в системе (6.5), т. е. равно трем. Коэффициентами в целевой функции двойственной задачи являются свободные члены системы уравнений (6.5), т.е. числа 12, 24, 18. Целевая функция исходной задачи (6.4) – (6.6) исследуется на максимум, а система условий (6.5) содержит неравенства. Поэтому в двойственной задаче целевая функция исследуется на минимум. Так как все три переменные исходной задачи (6.4) – (6.5) принимают только лишь неотрицательные значения, то в системе условий двойственной задачи должны быть три неравенства. Следовательно, для задачи (6.4) – (6.5) двойственная задача такова: найти минимум функции
Значение целевой функции в задачах равно 34.8
11.2. Решение задач линейного программирования с использованием программного обеспечения MATLAB
В состав MATLAB входит Optimization Toolbox, предназначенный для решения линейных и нелинейных оптимизационных задач. Задача линейного программирования состоит в нахождении вектора x, который минимизирует целевую линейную функцию fTx при условии A X≤ B; X≥0, где с =(с1, c2,…,cn) представляет собой n-мерный вектор, составленный из коэффициентов целевой функции, причем cT – транспонированная вектор- строка; x=(x1. xn) – n –мерный вектор переменных решений, B=[b1 b2 m-мерный вектор свободных членов bm] Beq=[beq1 … beqr] ограничения в виде равенств; двусторонние покомпонентные ограничения в векторной форме lb≤x≤ub A= Пример: задача составления рациона питания Имеются 3 продукта П1, П2 и П3 разной цены, каждый из которых содержит определенное количество питательных ингридиентов И1, И2, И3, И4. Известно, что в день требуется: И1не менее 250, И2 не менее 60, И3 не менее 100 и И4 не менее 220. Требуется минимизировать затраты на приобретение продуктов. Очевидно, что количество приобретаемых процессов не может быть отрицательным.. Записываем целевую функцию, матрицу A, векторы b и lb в соответствии с требованиями Toolbox, обозначив искомые количества продуктов через x1, x2 и x3 соответственно. Поскольку линейные ограничения содержат «меньшк или равно», а количество ингредиентов в рационе не может быть менее заданных величин, то следует изменить знаки обеих частей системы.При вызове программы linprog вместо неиспользуемых ограничение (нет ограничений в виде равенств) задайте пустые массивы, обозначаемые в MATLAB пустыми скобками. Программа ration % задание матрицы и вектора правой части системы неравенств A=[4 6 15 2 2 0 5 3 4 7 3 12] A=-A; b=[250 60 100 220]; b=-b; % Определение коэффициентов целевой функции f=[44; 35; 100]; % Задание ограничений снизу на переменные lb=[0; 0; 0]; % решение и вывод результата в командное окно x=linprog(f,A,b,[],[],lb)
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.66.224 (0.007 с.) |

 f (c,x)=
f (c,x)=  (6.3)
(6.3)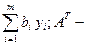 транспонированная матрица A.
транспонированная матрица A. при заданных ограничениях, то dс(х*)/dbi = уi*, i = 1,2,..., т.
при заданных ограничениях, то dс(х*)/dbi = уi*, i = 1,2,..., т.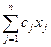 ).
).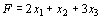 (11.4)
(11.4)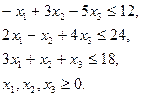 (6.5)
(6.5) и
и 
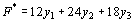 при условиях
при условиях