Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические постановки задач, приводящие к моделям линейного программированияСодержание книги
Поиск на нашем сайте
Задачи линейного программирования относятся к категории оптимизационных. Они находят широкое применение в различных областях практической деятельности: при организации работы транспортных систем, в управлении промышленными предприятиями, при составлении проектов сложных систем. Многие распространенные классы задач системного анализа, в частности, задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарного планирования, межотраслевого баланса укладываются в рамки моделей линейного программирования. Несмотря на различные области приложения, данные задачи имеют единую постановку: найти значения переменных x1, …, xn, доставляющие оптимум заданной линейной формы z=c1x1 + c2x2+… + cnxn при выполнении системы ограничений, представляющих собой также линейные формы. Линейное программирование – раздел теории оптимизации, посвященный изучению и решению экстремальных задач, в которых линейная функция и ограничения, задающие допустимое множество, являются линейными. Родоначальником линейного программирования считают д-ра физ.-мат. наук, лауреата Государственной и Нобелевской премий Л.В. Канторовича, который в 30-е годы XX века предложил метод решения экономических задач (в частности, задачи раскроя фанеры). Л.В. Канторович разработал метод разрешающих множителей для решения задачи линейного программирования. В последующем, в 50-е гг. XX в. независимо от Канторовича метод решения задачи линейного программирования (так называемый симплекс-метод) был развит американским математиком Дж. Данцигом, который в 1951 г. и ввел термин «линейное программирование». Слово «программирование» объясняется тем, что неизвестные переменные, которые отыскиваются в процессе решения задачи, обычно определяют программу (план) действий некоторого объекта, например, промышленного предприятия. Слово «линейное» отражает линейную зависимость между переменными. Приведем простейший пример задачи линейного программирования. Предположим, что для изготовления двух видов продукции P1 и P2 используют четыре вида ресурсов S1, S2, S3 и S4. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, прибыль, получаемая от единицы продукции, приведены в таблице. Расход ресурсов на производство продукции
Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.
и ряд ограничений (в данном случае диктуемых ограниченными запасами ресурсов): х1 + 3х2 ≤ 18; 2 х1+ х2 ≤ 16; (2) х2 ≤ 5;. 3x1 ≤21. x1≥0, x2≥0, Область доступных решений ЗЛП в стандартной форме образуется перечислением m множеств. Каждое из них определяется соответствующим неравенством ai1x1+…+ ainxn £ bi, i= и представляет собой полупространство, лежащее по одну сторону от гиперплоскости ai1x1+…+ ainxn = bi, i= Пересечение указанных полупространств является многогранником, который и будет областью допустимых решений задачи и обозначается как X. Линии уровня минимизируемой функции z = с1x1+…+cnxn = const (3) образуют семейство параллельных плоскостей. Вектор нормали к этим плоскостям c = {c1, c2, …, cn}T определяет направления возрастания нулевой функции z, а противоположный вектор –с определяет направление убывания функции z.
Выберем из семейства (3) любую плоскость, пересекающую многогранник допустимых решений X, и будем смещать ее в направлении с, если решается задача максимизации целевой функции z, и в направлении -с, если решается задача минимизации. Будем смещать эту плоскость до такого предельного положения, когда многогранник X окажется весь по одну сторону от неё и хотя бы одна их точек X все еще будет принадлежать нашей плоскости. Эти точки, или точка, лежащие на плоскости и будут решением задачи минимизации целевой функции z, и x* решением, соответственно, задачи максимизации функции z (рис. 1). Заметим, что множество точек, удовлетворяющих неравенству (1), т.е. множество допустимых решений X, может быть пустым, ограниченным и неограниченным. В первом случае задача не имеет решения.
Рис.2 Пример пустой области допустимых решений (X)
Во втором случае ЗЛП заведомо разрешима и имеет либо единственное решение (рис.1), совпадающее с одной из вершин допустимого многогранника X, либо бесконечное множество решений (рис.3) – ребро или грань многогранника, параллельные плоскостям семейства (3).
Рис.3 Пример ЗЛП, имеющий бесконечное множество решений (ребро АВ многогранника допустимых решений ABCDE) Если допустимое множество решений ЗЛП неограниченно, ответ на вопрос о существовании ее решения для задачи максимизации зависит от того, ограничена сверху на этом множестве целевая функция z или нет. Если ограничена, задача разрешима, причем возможны те же ситуации, что и во втором из рассмотренных выше случаев. Если нет – решение отсутствует (рис.4). Для задачи минимизации, в случае неограниченного множества допустимых решений X, ответ на вопрос о существовании решения ЗЛП
Рис.4 - Пример ЗЛП, имеющей неограниченное множество допустимых решений. зависит от того, ограничена снизу на множестве X целевая функция z или нет. Возникающие ситуации те же что и у задач максимизации. Простые ЗЛП допускают геометрическую интерпретацию, позволяющую непосредственно из графика получить решение и проиллюстрировать идею решения более сложных задач линейного программирования. Графическое решение задачи приведено на рисунке 3.1. Ограничения здесь задают область допустимых решений в форме (заштрихованного) четырехугольника, а семейство (пунктирных) прямых, представляет собой линии уровня целевой функции F. Существует два крайних положения линии уровня, когда она «касается» допустимого множества. Этим двум положениям в данном случае соответствуют две точки «касания» -начало координат (0, 0) и точка (6, 4). Первая из этих точек - точка минимума, а вторая - максимума данной функции F вида (1) на допустимом множестве (2). В случае большего числа разнородных ограничений графическая интерпретация задачи затруднена, поэтому задачу представляют в математической форме и используются специальные методы. Постановка данной задачи выглядит следующим образом. Имеется множество переменных X = (x1, х2,..., хn). Целевая функция линейно зависит от управляемых параметров:
Имеются ограничения, которые представляют собой линейные формы
Задача линейного программирования формулируется так: Определить максимум линейной формы F(x1,…,xn)=max(c1x1+…+cnxn) (3.3) при условии, что точка (х1, х2,..., хn) принадлежит некоторому множеству D, которое определяется системой линейных неравенств
Любое множество значений (х1*, х2*,..., хn*), которое удовлетворяет системе неравенств (3.4) задачи линейного программирования, является допустимым решением данной задачи. Если при этом выполняется неравенство c1х1o+ c2 х2o+..+ cn хno ≥ c1х1+ c2 х2+..+ cn хn для всего множества значений x1, х2,..., хn, то значение х1o..хno является оптимальным решением задачи линейного программирования. Задачу линейного программирования удобно представлять в векторной форме, тогда она будет выглядеть следующим образом: найти max F(x) = max (c Tx) при условии А Х ≤ Ро; Х≥0, где с = (с1,с2,..., сn) представляет собой n -мерный вектор, составленный из коэффициентов целевой функции, причем с T-транспонированная вектор-строка; х = (х1, х2,..., хп) - п-мерный вектор переменных решений;
Матрица А размером (m×n) - матрица, составленная из коэффициентов всех линейных ограничений:
Каноническая задача линейного программирования заключается в минимизации (максимизации) линейной целевой функции F(x) = clx1+c2x2+... + cnxn при ограничениях a11х1 +а12х2 +...+а1пхn=b1 а21х1 +а22х2 +...+а2пхn=b1… … аm1х1 +аm2х2 +...+аmпхn=b1 xt,x2,...,xn>0. где с[,с2,...,сп - коэффициенты целевой функции, atJ, i = \, 2,...,n,j = 1, 2,...,m -коэффициенты системы ограничений, а b1,bг,...,bn - свободные члены, которые считаются неотрицательными. Вектор X = (xi, х2,..., xj, удовлетворяющий ограничениям задачи ЛП, называется допустимым решением или планом. Допустимый план X* =(xl,x'2,...,x'n), при котором целевая функция задачи ЛП принимает максимальное (минимальное) значение, называется оптимальным планом. Иными словами, каноническая задача линейного программирования (ЛП) состоит в нахождении среди всех решений выписанной выше системы линейных уравнений такого ее неотрицательного решения, на котором достигает своего минимального (максимального) значения линейная целевая функция z от и переменных. В задаче линейного программирования общего вида вместо некоторых (всех) равенств в ограничениях записаны нестрогие неравенства в ту или другую сторону; при этом условие не отрицательности переменных может отсутствовать для части или же для всех переменных. Известно, что решение любой задачи линейного программирования может быть сведено к решению канонической задачи, представляемой в форме (1) или (4). Линейное программирование (ЛП) первоначально развивалось как направление, разрабатывающее новые подходы к решению задач минимизации выпуклых функций на выпуклом множестве (см. выпуклое программирование). Понятие целевой функции, удобное для приложений, сформировалось позднее. Наиболее простым и распространенным методом решения канонической задачи линейного программирования до сих пор является симплекс-метод, предложенный в 40-е годы прошлого века Дж. Данцигом. Геометрически идею симплекс-метода в упрощенной форме можно выразить следующим образом. Допустимым множеством в задаче линейного программирования является некоторое многогранное множество и-мерного векторного пространства (в частном случае n = 2 - это выпуклый и не обязательно ограниченный многоугольник). Работа симплекс-метода начинается с некоторой начальной вершины (начального опорного плана) многогранного множества. Специальным образом выясняется, нет ли среди соседних вершин такой, в которой значение целевой функции лучше? Если такая вершина находится, то она и принимается за следующее приближение. После этого вновь исследуются соседние вершины для полученного приближения и т. д. до тех пор, пока не будет получена вершина, среди соседних вершин которой не существует вершины с лучшим значением целевой функции. Такая вершина является оптимальной. Она соответствует оптимальной точке (оптимальному решению) задачи линейного программирования. В настоящее время разработан широкий круг различных численных методов решения задач линейного программирования, каждый из которых учитывает ту или иную специфическую особенность имеющейся задачи линейного программирования. Кроме симплекс-метода имеются и другие методы решения специальных задач ЛП: метод потенциалов, Венгерский метод, двойственный симплекс-метод, метод обратной матрицы (модифицированный симплекс-метод) и др. В настоящее время линейное программирование представляет собой область математики, посвященную разработке теории и численных методов решения экстремальных задач с линейными целевыми функциями и линейными ограничениями в виде систем равенств и/или неравенств. С применением линейного программирования решается широкий круг задач экономического характера: задачи о комплексном использовании сырья, рационального раскроя материалов, задачи загрузки оборудования, размещения заказов по однородным предприятиям, задачи о смесях, задачи текущего производственного планирования (статическая модель), задачи перспективного оптимального планирования, транспортная задача.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 158; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.128.17 (0.007 с.) |

 (1)
(1) (1)
(1) Рис1. Геометрическая интерпретация ЗЛП в стандартной форме
Рис1. Геометрическая интерпретация ЗЛП в стандартной форме


 (3.1)
(3.1) где
где  . (3.2)
. (3.2) (3.4)
(3.4)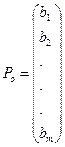 - m -мерный вектор свободных
- m -мерный вектор свободных  членов ограничений;
членов ограничений;